Teorema de Tales de Mileto: explicación, primero, segundo y ejemplos
¿Qué es el Teorema de Tales?
El teorema de Tales de Mileto en realidad hace alusión a varios teoremas de geometría atribuidos al sabio de la Antigua Grecia Tales de Mileto, quien vivió desde el 624 hasta el 546 aC en Mileto, actual Turquía.
Además de matemático y geómetra, Tales fue filósofo reconocido por su gran agudeza. De él se cuenta que consiguió medir la altura de la Gran Pirámide mediante el uso de uno de sus teoremas.
El primer teorema de Tales se refiere a los segmentos que un grupo de rectas paralelas determina en dos rectas en el plano. Estos segmentos guardan una relación de proporcionalidad, como se verá en breve, misma que se hace extensiva a los lados de dos triángulos, siempre que se cumplan ciertas condiciones.
Este teorema es sumamente útil en la práctica, pues permite determinar la altura de estructuras muy altas o de difícil acceso, sin necesidad de medirlas directamente. Esto fue precisisamente lo que Tales hizo cuando midió la altura de la Gran Pirámide.
Por su parte, el segundo teorema de Tales vincula puntos que pertenecen a una circunferencia con un triángulo rectángulo inscrito en ella, cuya hipotenusa coincide con su diámetro.
Primer teorema de Tales
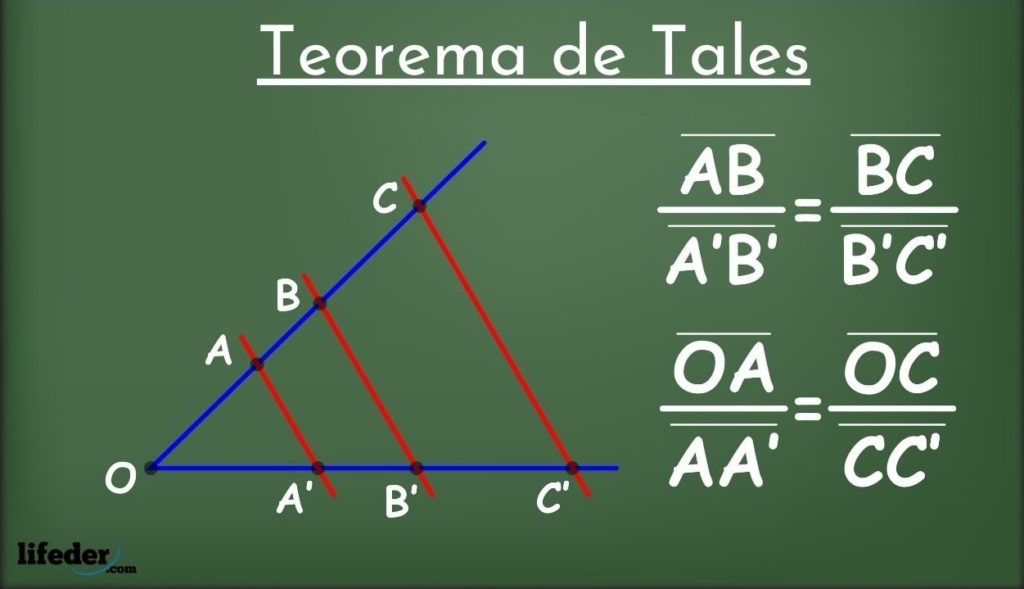
Sean dos rectas en un plano, llamadas L1 y L2 (en azul en la figura 1) y un grupo de rectas paralelas entre sí (en rojo) que intersectan a L1 y L2.
Las rectas paralelas dividen en segmentos a las rectas L1 y L2: AB, A’B’, BC, B’C’ y así sucesivamente. Entre los segmentos enfrentados se establece la siguiente relación de proporcionalidad:
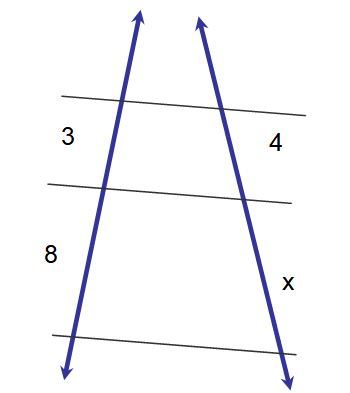
3x = 32
x = 32/3 ≈ 10.7
El teorema de Tales para triángulos semejantes
El teorema se puede extender a los triángulos de la siguiente manera: supongamos que se tiene un triángulo ABC sobre el cual se traza un segmento paralelo a uno de sus lados. De esta manera se obtienen dos triángulos semejantes: ABC y DEC, cuyos ángulos internos son congruentes, es decir, tienen igual medida.
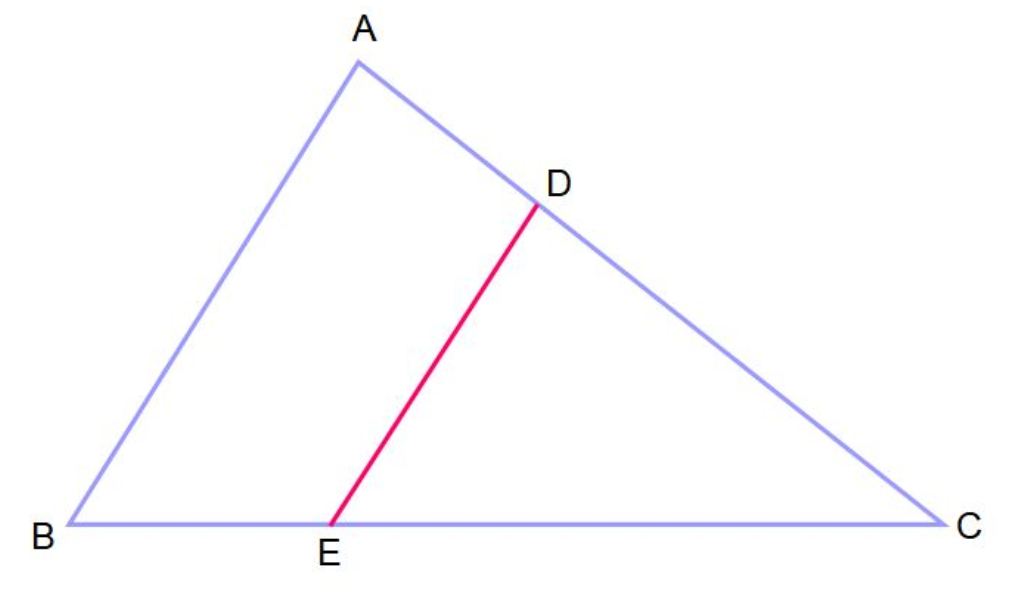
Cuando se tienen dos triángulos dispuestos de esta forma, se dice que están en posición de Tales.
Una relación de proporcionalidad entre los segmentos se plantea de la misma forma que para las rectas paralelas:
Que es equivalente a esta otra, entre los lados correspondientes de cada triángulo, también llamados lados homólogos:
A continuación un ejemplo en el que se puede aplicar el teorema de Tales para triángulos semejantes y averiguar cuanto vale el lado incógnita x.
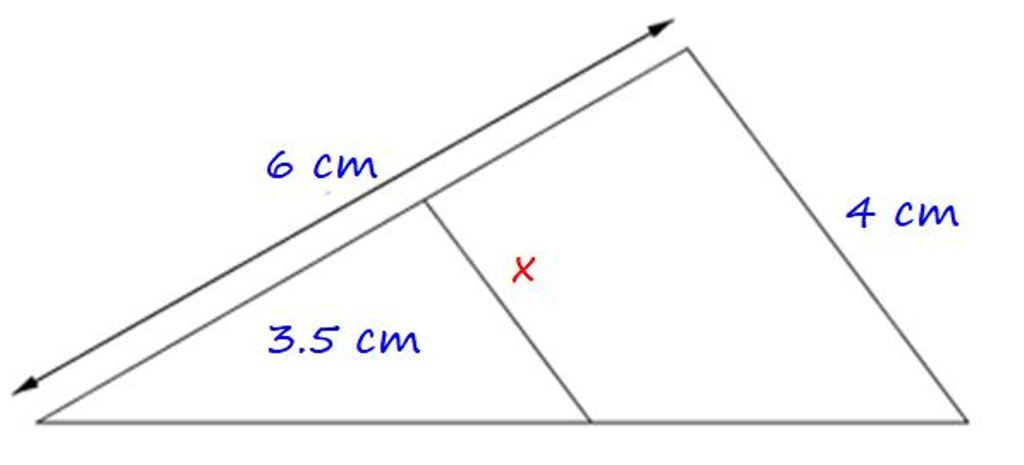
Los triángulos formados son semejantes, pues tienen un ángulo común y los lados x y 4 cm son paralelos.
Por lo tanto la proporcionalidad entre los lados correspondientes es:
x = (4×3.5) ÷ 6 cm = 2.3 cm
Segundo teorema de Tales
Este teorema se refiere a un triángulo cuyos vértices son puntos que pertenecen a una circunferencia, lo que quiere decir que está inscrito en ella.
En este caso, el teorema establece que siempre que la hipotenusa se corresponda al diámetro de la circunferencia, el triángulo así trazado es rectángulo, es decir, uno de sus ángulos internos mide 90º, tal como se aprecia en la figura 5 a la izquierda.
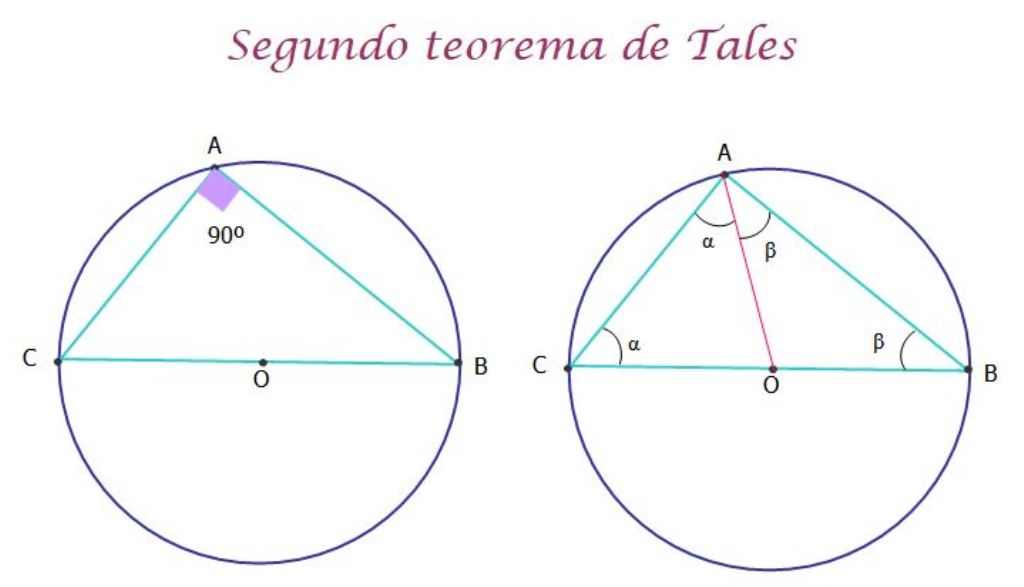
Demostración del segundo teorema de Tales
La demostración del teorema es muy sencilla. En la figura de arriba a la derecha, se ha trazado el segmento AO en rojo, para formar los dos triángulos AOC y AOB, los cuales son isósceles, ya que los lados OA, OC y OB son radios de las circunferencias y por lo tanto miden igual.
De esta manera, los triángulos tienen dos ángulos iguales, que son respectivamente α y β. Ahora, para el triángulo original ABC, como para todo triángulo, se cumple que la suma de las medidas de sus ángulos internos es igual a 180º, por lo tanto:
α + (α + β) + β = 180º
De allí que:
2α + 2β = 180º
Por lo tanto:
2(α + β) = 180º
α + β = 90º
Lo cual comprueba que el triángulo ABC tiene un ángulo interno de 90º y por lo tanto es un triángulo rectángulo.
Ejemplo
En la siguiente figura el triángulo ABC es isósceles y rectángulo (triángulo isorectángulo), siendo el perímetro de la circunferencia igual a 25 cm. ¿Cuánto miden los segmentos AC y AB?
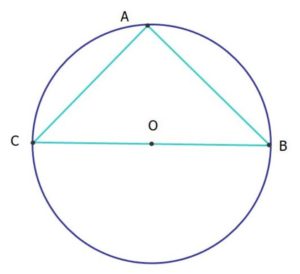
El perímetro de la circunferencia es su longitud L, dada en función de su diámetro D mediante la fórmula:
L = πD
Por lo tanto el diámetro, que es el segmento CB, mide:
D = CB = L/π = 25 cm/ π = 7.96 cm.
Puesto que el triángulo es isósceles, esto significa que sus ángulos agudos miden 45º cada uno. Como la hipotenusa del triángulo es el diámetro de la circunferencia, se puede emplear una razón trigonométrica de 45º, por ejemplo:
sen 45º = AC/CB
AC = CB × sen 45º = 7.96 cm× sen 45º = 5.64 cm
El lado AB tiene la misma medida: 5.64 cm, ya que el triángulo es isósceles.
Aplicaciones del Teorema de Tales
El primer teorema de Tales se puede usar para conocer distancias que no son fácilmente medibles. Se cuenta que Tales viajó a Egipto y allí determinó, de una forma muy ingeniosa, la altura de la Gran Pirámide.

Para ello fue necesario medir la sombra de esta sobre el suelo del desierto, más la altura y la sombra de una estaca clavada verticalmente en él. Así se forman dos triángulos semejantes, pues los rayos del Sol tienen incidencia paralela.
En la figura, la altura de la pirámide es y1 y su sombra es x1, mientras que la altura de la estaca es y2 (algunos cronistas afirman que Tales usó su propia estatura) y su sombra es x2. Como los triángulos son semejantes, se forma la siguiente relación de proporcionalidad:
Siendo muy sencillo despejar la altura de la pirámide y1:
y1 = x1∙ (y2 ÷ x2)
Referencias
- Alexander, D. 2013. Geometría. 5ta. Edición. Cengage Learning.
- Requena, B. Teorema de Tales. Recuperado de: universoformulas.com.
- Salón Matemático. Tales de Mileto y la Gran Pirámide. Recuperado de: salonmatemático.com
- Superprof Material Didáctico. Los teoremas de Tales de Mileto. Recuperado de: superprof.es.
- Teorema de Thales y semejanza. Dos problemas muy antiguos. Recuperado de: edu.xunta.gal.
