Fuerza de cizallamiento: fuerzas de superficie y másicas
La fuerza de cizallamiento es una fuerza compuesta que se caracteriza por ser paralela a la superficie sobra la que se ejerce y tiende a dividir al cuerpo, desplazando entre sí las secciones que resultan del corte.
Esquemáticamente está representada en la figura 1, en la que se muestra una fuerza cortante aplicada sobre dos puntos distintos de un lápiz de madera. La fuerza cortante requiere a su vez de dos fuerzas paralelas y opuestas, que dependiendo de su intensidad, son capaces de deformar al lápiz o definitivamente fracturarlo.
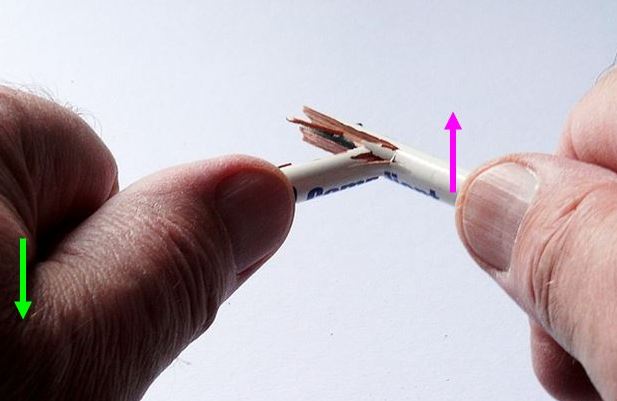
Entonces, aunque se hable de la fuerza de cizallamiento en singular, en realidad se aplican dos fuerzas, ya que la fuerza de cizallamiento es una fuerza compuesta. Estas fuerzas constan de dos fuerzas (o más, en casos complejos) aplicadas en distintos puntos de un objeto.
Dos fuerzas de la misma magnitud y sentido contrario, pero con líneas de acción paralelas, constituyen un par de fuerzas. Los pares no proporcionan traslación a los objetos, pues su resultante es nula, pero sí proporcionan un torque neto.
Con un par se hacen rotar objetos como el volante de un vehículo, o se pueden deformar y romper, como en el caso del lápiz y de la tabla de madera mostrada en la figura 2.

Índice del artículo
Las fuerzas compuestas forman parte de las llamadas fuerzas de superficie, justamente porque se aplican en la superficie de los cuerpos y no están relacionadas en modo alguno con su masa. Para aclarar el punto comparemos estas dos fuerzas que actúan frecuentemente sobre los objetos: el peso y la fuerza de rozamiento.
La magnitud del peso es P = mg y como depende de la masa del cuerpo, no es una fuerza de superficie. Se trata de una fuerza másica, y el peso es el ejemplo más característico.
Ahora bien, el rozamiento depende de la naturaleza de las superficies de contacto y no de la masa del cuerpo sobre el que actúa, por lo tanto es un buen ejemplo de las fuerzas superficiales de aparición frecuente.
Las fuerzas superficiales pueden ser simples o compuestas. Ya hemos visto un ejemplo de fuerza compuesta en la fuerza de cizallamiento, y por su parte, el rozamiento se representa como una fuerza simple, ya que basta con una sola flecha para representarlo en el diagrama de cuerpo aislado del objeto.
Las fuerzas simples se encargan de imprimir cambios al movimiento de un cuerpo, por ejemplo sabemos que la fuerza de roce cinético entre un objeto en movimiento y la superficie sobre la cual se mueve, resulta en una reducción de velocidad.
Al contrario, las fuerzas compuestas tienden a deformar los cuerpos y en el caso de las cizallas o cizalladuras, el resultado final puede ser un corte. Otras fuerzas de superficie tales como la tensión o la compresión, alargan o comprimen al cuerpo sobre el cual actúan.
Cada vez que se corta el tomate para la preparar la salsa o se emplea una tijera para seccionar una hoja de papel, se aplican los principios descritos. Las herramientas de corte suelen tener dos hojas de metal afiladas para que apliquen la fuerza de cizallamiento sobre la sección transversal del objeto que se desea trocear.

Los efectos de la fuerza de cizallamiento dependen de la magnitud de la fuerza y del área sobre la cual actúa, por eso en ingeniería se utiliza mucho el concepto de esfuerzo de cizallamiento, el cual toma en cuenta tanto la fuerza como el área.
Este esfuerzo tiene otras acepciones tales como esfuerzo cortante o esfuerzo de corte y en construcciones civiles es sumamente importante considerarlo, puesto que muchas fallas en las estructuras provienen de la actuación de las fuerzas cortantes.
Su utilidad se comprende de inmediato al considerar la siguiente situación: supongamos que se tienen dos barras del mismo material pero distinto grosor que se someten a fuerzas cada vez mayores hasta romperlos.
Resulta evidente que para romper la barra más gruesa hay que aplicar mayor fuerza, sin embargo el esfuerzo es el mismo para cualquier barra que tenga la misma composición. Ensayos como este son frecuentes en ingeniería, dada la importancia que tiene la selección del material adecuado para que la estructura proyectada funcione de manera óptima.
Matemáticamente, si se denota al esfuerzo de cizalla como τ, a la magnitud de la fuerza aplicada como F y al área sobre la cual actúa como A, se tiene el esfuerzo cortante promedio:
τpromedio= F /A
Al ser el cociente entre fuerza y área, la unidad del esfuerzo en el Sistema Internacional es el newton/m2, llamado Pascal y abreviado como Pa. En el sistema inglés se utilizan la libra–fuerza/pie 2 y la libra-fuerza /pulgada2.
Ahora bien, en muchos casos el objeto sometido al esfuerzo de cizalla se deforma y luego recupera su forma original sin llegar a romperse, una vez que el esfuerzo haya dejado de actuar. Supóngase que la deformación consiste en un cambio de longitud.
En este caso el esfuerzo y la deformación son proporcionales, por lo tanto se puede plantear lo siguiente:
Esfuerzo cortante ∝ Deformación unitaria
El símbolo ∝ significa “proporcional a”y en cuanto a la deformación unitaria, se la define como el cociente entre el cambio de longitud, al cual se llamará ΔL y la longitud original, denominada Lo. De esta manera:
τ ∝ (ΔL / Lo)
Al ser un cociente entre dos longitudes, la deformación unitaria no tiene unidades, pero al colocar el símbolo de igualdad, la constante de proporcionalidad debe proveerlas. Llamando G a dicha constante:
τ =G (ΔL / Lo)
G recibe el nombre de módulo de cizalladura o módulo de corte. Tiene unidades de Pascal en Sistema Internacional y su valor depende de la naturaleza del material. Es posible determinar en el laboratorio tales valores, ensayando la acción de distintas fuerzas sobre muestras de composición variada.
Cuando se requiere determinar la magnitud de la fuerza de cizalladura a partir de la ecuación anterior, basta con sustituir la definición de esfuerzo:
τ = F /A =G (ΔL / Lo)
Y despejar:
F = A × G (ΔL / Lo)
Las fuerzas cortantes son muy frecuentes y sus efectos deben ser tomados en cuenta en numerosos aspectos de la ciencia y la tecnología. En las construcciones aparecen en los puntos de apoyo de las vigas, pueden surgir durante un accidente y romper un hueso y su presencia es capaz de alterar el funcionamiento de una maquinaria.
Actúan a gran escala sobre la corteza terrestre causando fracturas en las rocas y accidentes geológicos, gracias a la actividad tectónica. Por tanto también son responsables de modelar continuamente al planeta.
- Beer, F. 2010. Mecánica de materiales. 5ta. Edición. McGraw Hill. 7 – 9.
- Fitzgerald, 1996. Mecánica de Materiales. AlfaOmega. 21-23.
- Giancoli, D. 2006. Physics: Principles with Applications. 6tth Ed. Prentice Hall. 238-242.
- Hibbeler, R.C. 2006. Mecánica de materiales. 6ta. Edición. Pearson Educación. 22 -25
- Valera Negrete, J. 2005. Apuntes de Física General. UNAM. 87-98.
- Wikipedia. Shear Stress. Recobrado de: en.wikipedia.org.
