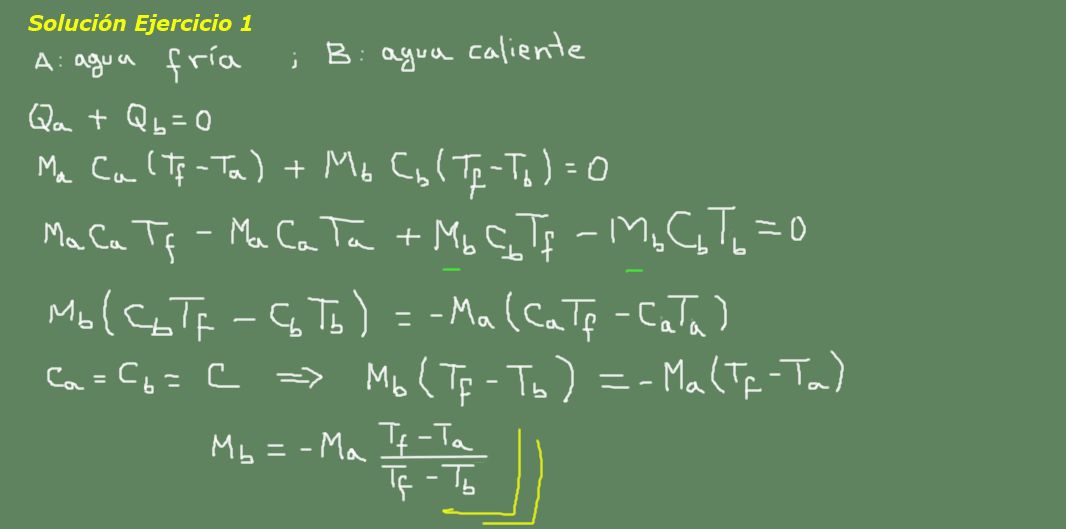Equilibrio térmico: ecuaciones, aplicaciones, ejercicios
El equilibrio térmico de dos cuerpos que están en contacto térmico, es el estado que se alcanza después de un tiempo suficientemente largo como para que las temperaturas de ambos cuerpos se igualen.
En termodinámica se entiende por contacto térmico de dos cuerpos (o dos sistemas termodinámicos) una situación en la que los cuerpos tienen contacto mecánico o están separados pero en contacto con una superficie que permite solo el paso de calor de un cuerpo al otro (superficie diatérmica).
En el contacto térmico no debe haber reacción química entre los sistemas en contacto. Solo debe haber intercambio de calor.
Situaciones cotidianas en las que hay intercambio de calor se presentan con sistemas tales como la bebida fría y el vaso, el café caliente y la cucharilla, o el cuerpo y el termómetro, entre muchos otros ejemplos.
Índice del artículo
- 1 ¿Cuándo dos o más sistemas están en equilibrio térmico?
- 2 Ecuaciones del equilibrio térmico
- 3 Aplicaciones
- 4 Ejercicios resueltos
- 5 Referencias
La segunda ley de la termodinámica establece que el calor siempre va del cuerpo de mayor temperatura al de menor temperatura. La transferencia de calor cesa en cuanto las temperaturas se igualan y se llega al estado de equilibrio térmico.
La aplicación práctica del equilibrio térmico es el termómetro. Un termómetro es un dispositivo que mide su propia temperatura, pero gracias al equilibrio térmico podemos conocer la temperatura de otros cuerpos, como el de un persona o animal.
El termómetro de columna de mercurio se coloca en contacto térmico con el cuerpo, por ejemplo debajo de la lengua, y se espera suficiente tiempo para que se alcance el equilibrio térmico entre el cuerpo y el termómetro y que su lectura no varíe más.
Cuando se llega a este punto, la temperatura del termómetro es la misma que la del cuerpo.
La ley cero de la termodinámica establece que si un cuerpo A está en equilibrio térmico con un cuerpo C y ese mismo cuerpo C está en equilibrio térmico con B, entonces A y B están en equilibrio térmico aun cuando entre A y B no exista contacto térmico.
Concluimos por tanto, que dos o más sistemas están en equilibrio térmico cuando tienen la misma temperatura.
Suponemos un cuerpo A con temperatura inicial Ta en contacto térmico con otro cuerpo B con temperatura inicial Tb. Suponemos también que Ta > Tb, entonces de acuerdo a la segunda ley el calor se transfiere de A hacia B.
Pasado un tiempo se alcanzará el equilibrio térmico y ambos cuerpos tendrán la misma temperatura final Tf. Esta tendrá un valor intermedio a Ta y Tb, es decir, Ta > Tf > Tb.
La cantidad de calor Qa transferida de A hacia B será Qa = Ma Ca (Tf – Ta), donde Ma es la masa del cuerpo A, Ca la capacidad calorífica por unidad de masa de A y (Tf – Ta) la diferencia de temperatura. Si Tf es menor que Ta entonces Qa es negativo, indicando que el cuerpo A cede calor.
Similarmente para el cuerpo B se tiene que Qb = Mb Cb (Tf – Tb); y si Tf es mayor que Tb entonces Qb es positivo, indicando que el cuerpo B recibe calor. Como el cuerpo A y el B están en contacto térmico entre ellos, pero aislados del medio ambiente, la cantidad total de calor intercambiada debe ser nula: Qa + Qb = 0
Luego Ma Ca (Tf – Ta) + Mb Cb (Tf – Tb) = 0
Desarrollando esta expresión y despejando la temperatura Tf se obtiene la temperatura final de equilibrio térmico.
Tf = (Ma Ca Ta + Mb Cb Tb) / (Ma Ca + Mb Cb).
Como caso particular considere el caso que los cuerpos A y B son idénticos en masa y en capacidad calorífica, en este caso la temperatura de equilibrio será:
Tf = (Ta + Tb) / 2 ↔ si Ma = Mb y Ca = Cb.
En algunas situaciones ocurre que cuando se colocan dos cuerpos en contacto térmico, el intercambio de calor ocasiona el cambio de estado o fase en alguno de ellos. Si esto sucede ha de tenerse en cuenta que durante el cambio de fase no se produce cambio de temperatura en el cuerpo que está modificando su estado.
De ocurrir el cambio de fase de alguno de los cuerpos en contacto térmico, se aplica el concepto de calor latente L, que es la energía por unidad de masa necesaria para el cambio de estado:
Q= L∙M
Por ejemplo, para fundir 1 kg de hielo a 0°C se requieren 333,5 kJ/kg y ese valor es el calor latente L de fusión del hielo.
Durante la fusión se cambia de agua sólida a agua líquida, pero ese agua mantiene la misma temperatura del hielo durante el proceso de fusión.
El equilibrio térmico forma parte de la vida diaria. Por ejemplo examinemos con detalle esta situación:
Una persona desea bañarse con agua tibia a 25°C. En un cubo coloca 3 litros de agua fría a 15°C y en la cocina calienta agua hasta 95 °C.
¿Cuántos litros de agua de agua caliente debe agregar al cubo de agua fría para tener la temperatura final deseada?
Solución
Supongamos A es el agua fría y B el agua caliente:
Planteamos la ecuación del equilibrio térmico, según se indica en la pizarra de la figura 3 y de allí despejamos la masa de agua Mb.
La masa inicial de agua fría la podemos obtener porque se sabe la densidad del agua, que es de 1Kg por cada litro. Es decir, que disponemos de 3 kg de agua fría.
Ma= 3kg
Entonces
Mb = – 3 kg*( 25°C – 15°C)/( 25°C – 95°C)= 0,43 kg
Entonces basta con 0,43 lts de agua caliente para obtener finalmente 3,43 litros de agua tibia a 25°C.
Se introduce un trozo de metal de 150 g de masa y con 95°C de temperatura a un recipiente que contiene medio litro de agua a temperatura de 18°C. Después de un rato se alcanza el equilibrio térmico y la temperatura del agua y del metal es de 25°C.
Supongamos que el recipiente con el agua y el trozo de metal es un termo cerrado que no permite intercambio de calor con el medio ambiente.
Obtener el calor específico del metal.
Solución
En primer lugar calcularemos el calor absorbido por el agua:
Qa= Ma Ca (Tf – Ta)
Qa= 500g 1cal/(g °C) (25°C – 18°C)= 3500 calorías.
Ese es el mismo calor cedido por el metal:
Qm= 150g Cm (25°C – 95°C)= -3500 calorías.
Entonces podemos obtener la capacidad calorífica del metal:
Cm= 3500 cal/ (150g 70°C) = ⅓ cal/(g °C).
Se tienen 250 c.c. de agua a 30°C. A ese agua que está en un termo aislante, se le agregan 25g de cubitos de hielo a 0°C, con el propósito de enfriarla.
Determinar la temperatura de equilibrio; es decir, la temperatura que quedará una vez que todo el hielo se haya fundido y el agua del hielo se haya calentado hasta igualar la del agua que inicialmente tenía el vaso.
Solución 3
Este ejercicio puede resolverse en tres etapas:
- La primera es la fusión del hielo que absorbe calor del agua inicial para fundirse y convertirse en agua.
- Luego se calcula el descenso de temperatura en el agua inicial, debido a que ha cedido calor (Qced0) para fundir el hielo.
- Por último, el agua fundida (proveniente del hielo) debe equilibrarse térmicamente con el agua que existía inicialmente.
Calculemos el calor necesario para la fusión del hielo:
Qf= L*Mh= 333,5 kJ/kg * 0,025kg = 8,338 kJ
Luego, el calor cedido por el agua para fundir el hielo es Qced= -Qf
Este calor cedido por el agua desciende su temperatura hasta un valor T’ que podemos calcular así:
T’= T0 – Qf/(Ma*Ca)= 22,02°C
Donde Ca es la capacidad calorífica del agua: 4,18 kJ/(kg °C).
Por último la masa de agua original que ahora está a 22,02°C cederá calor a la masa de agua fundida proveniente del hielo que está a 0°C.
Finalmente se alcanzará después del tiempo suficiente la temperatura de equilibrio Te:
Te= (Ma*T’ + Mh*0°C) / (Ma + Mh)= (0,25kg * 22,02°C + 0,025kg * 0°C) / (0,25kg + 0,025kg).
Obteniéndose finalmente la temperatura de equilibrio:
Te= 20,02 °C.
Un trozo de plomo de 0,5 kg sale del horno a una temperatura de 150°C, la cual está bastante por debajo de su punto de fusión. Ese trozo se coloca en un recipiente con 3 litros de agua a temperatura ambiente de 20°C. Determine la temperatura final de equilibrio.
Calcule también:
– Cantidad de calor entregada por el plomo al agua.
– Cantidad de calor absorbida por el agua.
Datos:
Calor específico del plomo: Cp= 0,03 cal/(g °C); calor específico del agua: Ca= 1 cal/(g °C).
Solución
En primer lugar determinamos la temperatura final de equilibrio Te:
Te = (Ma Ca Ta + Mp Cp Tp) / (Ma Ca + Mp Cp)
Te=20,65 °C
Luego la cantidad de calor cedido por el plomo es:
Qp= Mp Cp (Te – Tp)= -1,94 x 10³ cal.
El cantidad de calor absorbida por el agua será:
Qa= Ma Ca (Te – Ta)= +1,94x 10³ cal.
- Atkins, P. 1999. Química Física. Ediciones Omega.
- Bauer, W. 2011. Física para Ingeniería y Ciencias. Volumen 1. Mc Graw Hill.
- Giancoli, D. 2006. Physics: Principles with Applications. 6th.. Ed Prentice Hall.
- Hewitt, Paul. 2012. Conceptual Physical Science. 5th. Ed. Pearson.
- Resnick, R. (1999). Física. Vol. 1. 3ra Ed. en español. Compañía Editorial Continental S.A. de C.V.
- Rex, A. 2011. Fundamentos de Física. Pearson.
- Sears, Zemansky. 2016. University Physics with Modern Physics. 14th. Ed. Volume 1.
- Serway, R., Jewett, J. (2008). Física para Ciencias e Ingeniería. Volumen 1. 7ma. Ed. Cengage Learning.