Ejercicio resuelto
Cifras significativas: reglas, ejemplos, ejercicios resueltos
Se llama cifras significativas a la cantidad de dígitos que contiene la mantisa de un número. Cuantos más números tenga, con mayor precisión se conoce la cantidad. Como recordatorio, la mantisa es la cifra que acompaña a la potencia de 10 cuando se escribe el número en notación científica.
Por ejemplo, tomemos al número 0.00376, que se escribe como 3.76 x 10 -3. La mantisa es 3.76 y el número tiene un total de 3 cifras significativas. El número 0.129 también tiene 3 cifras significativas, mientras que 4.5 tiene solamente 2.

¿Y qué sucede cuando el número es entero? Significa que se le conoce con toda la precisión posible, en otras palabras, tiene precisión infinita. Por ejemplo, al contar personas, animales u objetos como libros y teléfonos, el resultado es un número entero y preciso.
Si decimos que en una sala de cine hay 110 personas viendo una película, este es el número exacto, ni más ni menos, y tiene 3 cifras significativas.
Las cifras significativas se manejan mediante algunas reglas sencillas que se memorizan con un poco de práctica, como vamos a ver seguidamente.
Índice del artículo
- 1 Reglas para determinar las cifras significativas de un número
- 2 Ejemplos
- 3 Reglas para redondear números
- 4 Referencias
Los ceros precedentes no cuentan como una cifra significativa, así que 0.045 y 4.5 tienen ambos 2 cifras significativas, ya que estas comienzan a contarse desde la izquierda y partiendo del primer dígito diferente de cero.
Regla 2
Los ceros posteriores (a la derecha) al primer dígito significativo sí cuentan como cifra significativa (siempre y cuando se justifique por la precisión del instrumento de medida).
Finalmente, los ceros que están en medio también se cuentan como dígito significativo.
Para los números escritos en notación científica, todas las cifras de la mantisa son significativas, y el exponente no influye en la precisión.
Cuando se hacen operaciones con decimales, por ejemplo al calcular áreas u otras operaciones semejantes, el resultado debe tener igual número de cifras significativas que la cantidad con menor número de cifras significativas que participó en la operación. Esta regla es válida para cualquier operación aritmética.
El signo del número no influye en su cantidad de cifras significativas.
Veremos enseguida algunos ejemplos de esta y todas las demás reglas.
Encontrar cuántas cifras significativas hay en cada uno de estos números.
a) 876
b) 1000.68
c) 0.00005026
d) 4.8
e) -6.99
Respuestas
a) 876 tiene 3 cifras significativas.
b) 1000.68 tiene 6 cifras significativas, ya que los ceros en medio cuentan como tales.
c) En cambio 0.00005026 tiene 4 cifras significativas. Nótese que los 5 ceros a la izquierda del 5 no se cuentan como cifra significativa, en cambio el 0 que está entre el 5 y el 2 sí.
d) 4.8 tiene 2 cifras significativas.
e) -6.99 tiene 3 cifras significativas.
Es frecuente tomar medidas con instrumentos de medición, como cintas métricas, relojes, termómetros, balanzas y así por el estilo. ¿Con cuántas cifras significativas debemos reportar las cantidades que medimos de esta forma?
Respuesta
Depende de la apreciación del instrumento con que se mida. Pongamos un ejemplo: medir el diámetro externo de un tubo, con una regla graduada y con vernier o pie de rey.
El vernier es un instrumento que mide con mucha precisión las longitudes porque tiene una pequeña escala extra, llamada nonio, que permite una mayor finura, por así decirlo, al medir.
Es más preciso que una regla graduada porque con él podemos conocer más cifras significativas de una determinada longitud.
Por eso no tiene sentido reportar un perímetro de, digamos, 35.88 cm si lo medimos con cinta métrica, ya que este instrumento no es suficientemente preciso como para reportar tantos dígitos significativos.
La apreciación A de la cinta métrica viene dada por:
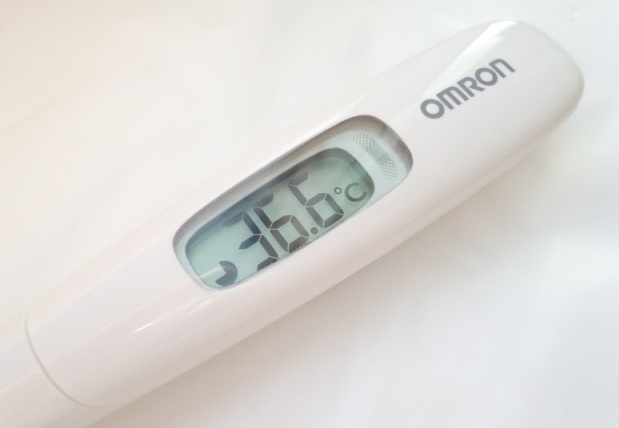
¿Cuántas cifras significativas tiene la lectura hecha con el termómetro digital?
Respuesta
El termómetro de la figura ofrece lecturas de la temperatura con tres dígitos. Sin embargo, en la medida mostrada, de 36.6 ºC, solamente son precisos los dos primeros dígitos de izquierda a derecha, ya que el decimal viene afectado por el error de apreciación del instrumento, que suele indicarse en la parte de atrás del mismo o en su manual de operaciones.
Lo usual para el tipo de instrumento digital mostrado es un error de apreciación de 0.1 ºC. Esto es suficiente para estar seguros de que no se tiene fiebre.
Cuando se usa una calculadora para realizar cálculos con medidas obtenidas, no es correcto dar el resultado utilizando todos los dígitos que aparecen en la pantalla.
Solamente se retienen aquellos que se conocen con precisión, pues solo esos tienen verdadero significado. Entonces se hace necesario redondear los resultados para se ajusten a la cantidad de cifras conocidas con precisión. Estas reglas son:
-Si el número que le sigue al dígito que se va a retener es igual o mayor que 5, a dicho dígito se le suma 1.
Por ejemplo, al redondear 3.786 para que tenga dos decimales, queremos retener las cifras hasta el 8. Dado que el número que le sigue (6) es mayor que 5, el 8 pasa a ser 8 + 1 = 9 y el número queda como 3.79.
-Cuando el número siguiente al dígito que se va a retener es menor que 5, el dígito queda igual.
Si queremos redondear 1.27924 para que tenga solamente 3 decimales, esto se consigue llegando hasta el 9, el cual es seguido de un 2. Como el 2 es menor que 5, estos decimales desaparecen y el número redondeado queda 1.279.
Ejercicio resuelto
Una mesa de comedor tiene la forma y dimensiones indicadas en la figura adjunta. Se pide calcular su área utilizando las reglas de las operaciones con cifras significativas.
Solución
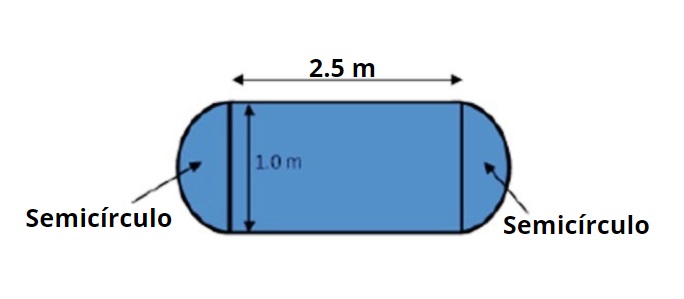
El área de la mesa se puede dividir en un área rectangular central y dos semicírculos, uno a cada lado, que juntos hacen 1 círculo completo.
Llamaremos A1 al área del rectángulo, dada por:
A1 = base × altura = 2.5 m x 1.0 m = 2.5 m2
Por su parte, el área del círculo, que equivale a la de 1 semicírculo multiplicado por 2 es:
A2 = π × radio2
El diámetro de cualquiera de los semicírculos es 1.0 m, por lo tanto el radio es 0.50 m. También se pudiera emplear directamente el diámetro para calcular el área, en este caso:
A2 = (π × diámetro2) / 4
En todo caso:
A2 = [π x (1.0 m)2] / 4 = 0.785398163 m2
Se utilizaron todos los dígitos que ofreció la calculadora. Ahora sumamos A1 y A2 para el área total A de la mesa:
A = (2.5 + 0.785398163) m2 = 3.285398163 m2
Como las dimensiones de la mesa se conocen con 2 cifras significativas, no tiene sentido expresar el resultado con todos los decimales dados por la calculadora, la cual nunca da el número de cifras significativas de un resultado.
Lo que hay que hacer es redondear el área para que tenga igual número de cifras significativas que las dimensiones de la mesa, es decir, 2. Por lo tanto el resultado final se reporta así:
A = 3.3 m2
- Bauer, W. 2011. Física para Ingeniería y Ciencias. Volumen 1. Mc Graw Hill.
- Figueroa, D. (2005). Serie: Física para Ciencias e Ingeniería. Volumen 1. Cinemática. Editado por Douglas Figueroa (USB).
- Fisicalab. Cifras significativas y redondeo. Recuperado de: fisicalab.com.
- Giancoli, D. 2006. Physics: Principles with Applications. 6th. Ed Prentice Hall.
- Sears, Zemansky. 2016. University Physics with Modern Physics. 14th. Ed. Volume1.
