Carga radial: cómo se calcula, ejercicios resueltos
La carga radial es la fuerza que se ejerce perpendicularmente al eje de simetría de un objeto y cuya línea de acción pasa por este eje. Por ejemplo, una correa en una polea impone una carga radial sobre el cojinete o rodamiento del eje de la misma.
En la figura 1 las flechas amarillas representan fuerzas o cargas radiales sobre los ejes debido a la tensión de la correa que pasa por las poleas.
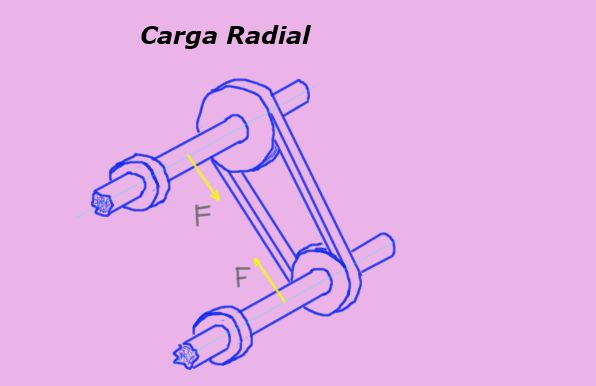
La unidad de medida de la carga radial en el sistema internacional o SI es el Newton (N). Pero también con frecuencia se usan otras unidades de fuerza para medirla, como el kilogramo-fuerza (Kg-f) y la libra fuerza (lb-f).
Índice del artículo
Para calcular el valor de la carga radial en los elementos de una estructura se deben seguir los siguientes pasos:
– Hacer el diagrama de fuerzas sobre cada elemento.
– Aplicar las ecuaciones que garanticen el equilibrio traslacional; es decir, que la sumatoria de todas las fuerzas sea nula.
– Considerar la ecuación de los torques o momentos de modo que se cumpla el equilibrio rotacional. En este caso la suma de todos los torques debe ser nula.
– Calcular las fuerzas para poder identificar las cargas radiales que actúan en cada uno de los elementos.
En la figura siguiente se muestra una polea por la que pasa una polea tensa con tensión T. La polea está montada sobre un eje que se apoya en dos chumaceras. El centro de una de ellas está a una distancia L1 del centro de la polea. En el otro extremo está la otra chumacera, a distancia L2.
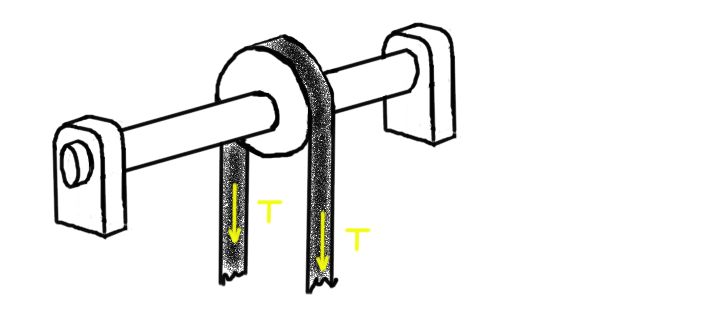
Determine la carga radial sobre cada una de las chumaceras, suponiendo que el peso del eje y la polea son bastante menores que la tensión aplicada.
Tome como valor para la tensión de la correa 100 kg-f y para las distancias L1= 1 m y L2=2 m.
Solución
En primer lugar se realiza un diagrama de las fuerzas que actúan sobre el eje.
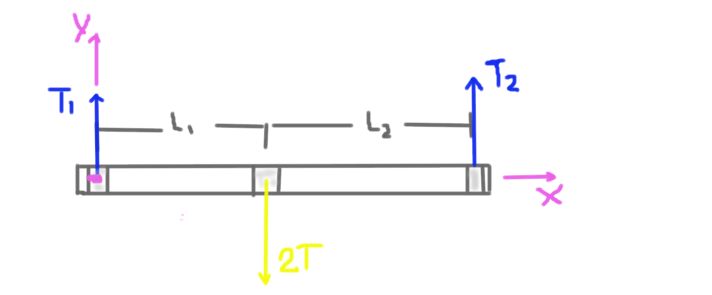
La tensión de la polea es T, pero la carga radial sobre el eje en la posición de la polea es 2T. No se toma en cuenta el peso del eje y la polea porque el enunciado del problema nos dice que es bastante menor que la tensión aplicada a la correa.
La reacción radial de los soportes sobre el eje está causada por las fuerzas o cargas radiales T1 y T2. También se indican en el diagrama las distancias L1 y L2 de los soportes al centro de la polea.
Se muestra también el sistema de coordenadas. El torque o momento total sobre el eje se calculará tomando como centro el origen del sistema de coordenadas y será positivo en la dirección Z.
Condiciones de equilibrio
Ahora se establecen las condiciones de equilibrio: sumatoria de fuerzas igual cero y sumatoria de torques igual cero.
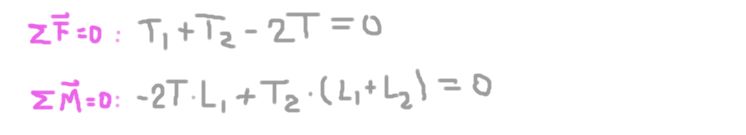
De la segunda ecuación se obtiene la reacción radial sobre el eje en el soporte 2 (T2), sustituyendo en la primera y despejando se obtiene la reacción radial sobre el eje en el apoyo 1 (T1).
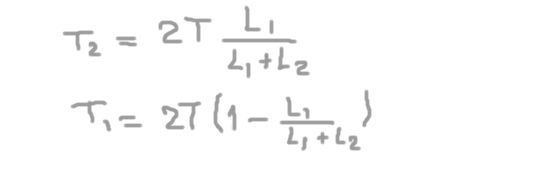
T1= (2/3)T= 66,6 kg-f
Y la carga radial sobre el eje en la posición del apoyo 2 es:
T2= (4/3)T= 133,3 kg-f.
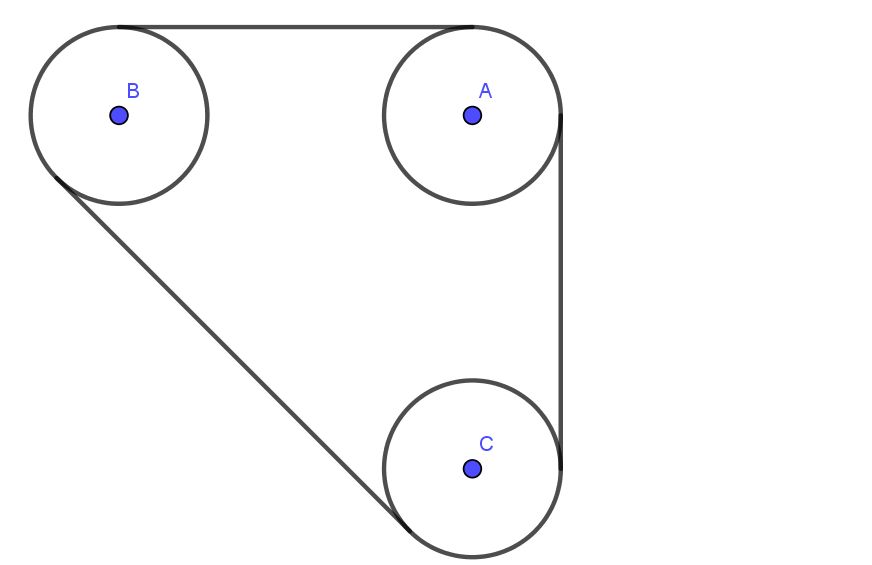
La figura siguiente muestra un sistema compuesto por tres poleas A, B, C todas del mismo radio R. Las poleas están conectadas mediante una correa que tiene una tensión T.
Los ejes A, B, C pasan por cojinetes lubricados. La separación entre los centros de los ejes A y B es 4 veces el radio R. Similarmente, la separación entre los ejes B y C también es 4R.
Determine la carga radial sobre los ejes de las poleas A y B, suponiendo que la tensión de la correa es 600N.
Solución
Se comienza por trazar un diagrama de las fuerzas que actúan sobre la polea A y sobre la B. Sobre la primera se tienen las dos tensiones T1 y T2, así como la fuerza FA que el cojinete ejerce sobre el eje A de la polea.
De forma similar, sobre la polea B se tienen las tensiones T3 , T4 y la fuerza FB que el cojinete ejerce sobre el eje de la misma. La carga radial sobre el eje de la polea A es la fuerza FA y la carga radial sobre el de la B es la fuerza FB.
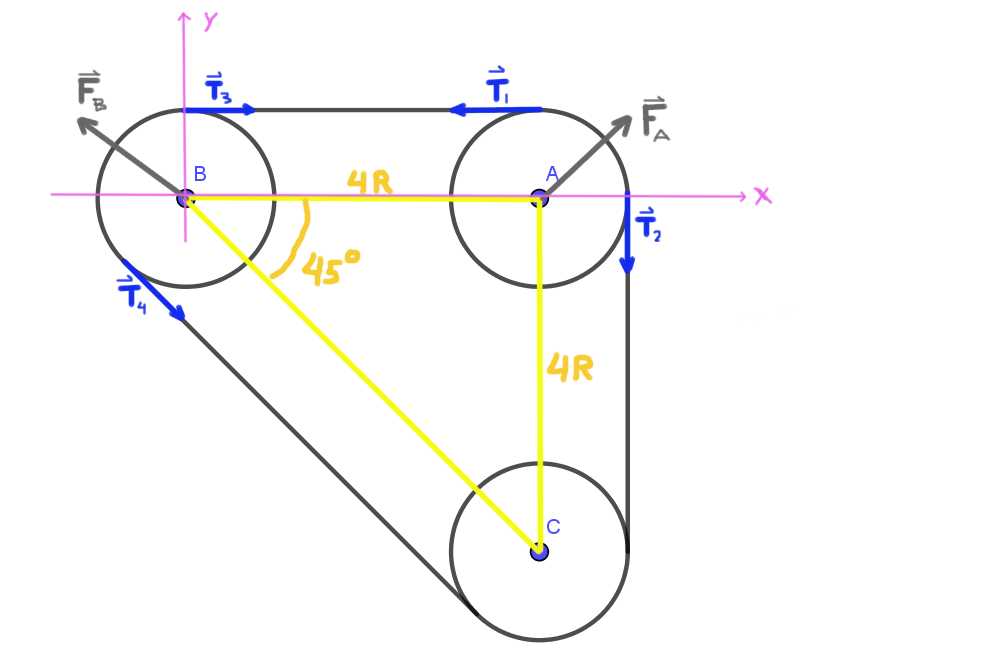
Como los ejes A, B, C forman un triángulo isorectángulo, el ángulo ABC es de 45°.
Todas las tensiones T1 , T2 , T3 , T4 mostradas en la figura tienen el mismo módulo T, que es la tensión de la correa.
Condición de equilibrio para la polea A
Ahora escribimos la condición de equilibrio para la polea A que no es otra cosa que la sumatoria de todas las fuerza que actúan sobre la polea A debe ser nula.
Separando las componentes X e Y de la fuerzas y sumando (vectorialmente) se obtiene el siguiente par de ecuaciones escalares:
FAX – T = 0; FAY – T = 0
Estas ecuaciones conducen a la siguiente igualdad: FAX = FAY = T.
Por lo tanto la carga radial tiene magnitud dada por:
FA = (T² + T² )1/2 = 21/2∙T = 1,41∙T = 848,5 N. con dirección de 45°.
Condición de equilibrio para la polea B
De forma similar, escribimos la condición de equilibrio para la polea B. Para la componente X se tiene: FBX + T + T∙Cos45° = 0
Y para la componente Y : FBY + T∙Sen45° = 0
De esta forma:
FBX = – T (1+2-1/2) y FBY = -T∙2-1/2
Es decir, que la magnitud de la carga radial sobre la polea B es:
FB = ((1+2-1/2)² + 2-1)1/2∙T = 1,85∙T = 1108,66 N y su dirección es 135°.
- Beer F, Johnston E, DeWolf J, Mazurek, D. Mecánica de materiales. Quinta edición. 2010. Mc Graw Hill. 1-130.
- Gere J, Goodno, B. Mecánica de materiales. Octava edición. Cengage Learning. 4-220.
- Giancoli, D. 2006. Physics: Principles with Applications. 6tth Ed. Prentice Hall. 238-242.
- Hibbeler R. Mecánica de materiales. Octava edición. Prentice Hall. 2011. 3-60.
- Valera Negrete, J. 2005. Apuntes de Física General. UNAM. 87-98.
