¿Qué son los números triangulares? Propiedades y demostraciones
Se conoce como números triangulares a la secuencia de números que se obtienen al hacer un arreglo o figura de puntos en forma de triángulo equilátero. Los primeros de la secuencia son: 1, 3, 6, 10, 15, 21,…
El primer número triangular es 1, el segundo es el 3, porque se obtiene de agregar una fila de dos puntos al anterior, para formar un triángulo equilátero de tres elementos.
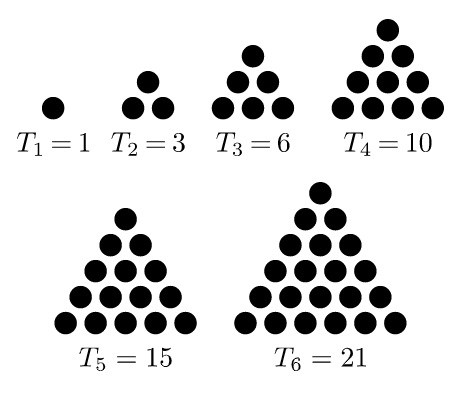
El tercero es el 6, el cual aparece al agregar una fila de tres puntos al arreglo anterior, de modo tal que se forma un triángulo de tres puntos por lado. El 10 de la secuencia se obtiene al agregar otra fila al arreglo anterior de modo que se forme un triángulo de cuatro puntos por lado.
La fórmula que permite encontrar el elemento n de la secuencia triangular, conocido el número triangular anterior es:
Tn = Tn-1 + n
La lista de los primeros seis números triangulares se consigue así:
–Primero: 1
–Segundo: 1 + 2 = 3
–Tercero: (1 +2) + 3 = 3 + 3 = 6
–Cuarto: (1 + 2 + 3) + 4 = 6 + 4 = 10
–Quinto: (1 + 2 + 3 + 4) + 5 = 10 + 5 = 15
–Sexto: (1 + 2 + 3 + 4 + 5) + 6 = 15 + 6 = 21
Índice del artículo
1.- El número triangular n-ésimo Tn de la secuencia de números triangulares es la mitad de n multiplicado por n+1:
Tn = ½ n (n+1)
2.- La suma del número triangular n-ésimo con el número triangular anterior, es decir el (n-1)-ésimo, es n elevado al cuadrado:
Tn + Tn-1= n2
3.- La diferencia del número triangular n-ésimo menos el triangular n-ésimo menos uno es n:
Tn – Tn-1 = n
4.- La suma de los n primeros números triangulares se denomina número tetraédrico Sn y es igual a la sexta parte del producto de n multiplicado por (n + 1) y multiplicado por (n + 2):
Sn= ⅙ n (n + 1) (n + 2)
5.- Todo número natural N es el resultado de la suma de tres números triangulares:
N = Δ1 + Δ1 + Δ3
Esta última propiedad o teorema, fue descubierta por el gran matemático Carl Friedrich Gauss en 1796, la cual anotó en su diario colocando la admiración griega Eureka! que significa “lo he conseguido”.
Esa era la misma palabra usada mucho antes por el griego Arquímedes cuando determinó el peso aparente de un cuerpo sumergido.
En esta relación se toma al número cero como triangular y puede haber repetición.
Probar que el número triangular n-ésimo es:
Tn = ½ n (n+1)
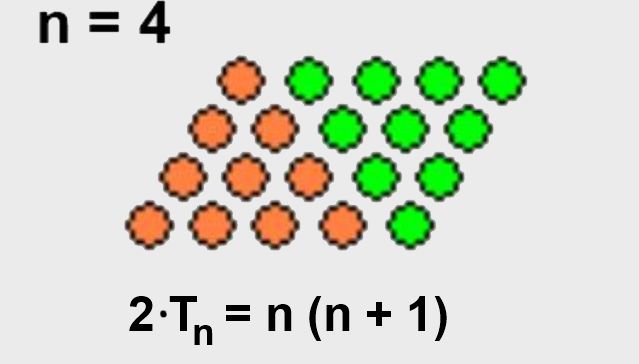
Es fácil deducir la fórmula anterior, si nos damos cuenta de que podemos agregar igual cantidad de puntos al arreglo triangular para que forme un cuadrilátero de puntos.
Como el número total de puntos del arreglo en forma de cuadrilátero es el número de filas n multiplicado por el número de columnas (n+1), entonces el arreglo triangular tendrá solo la mitad de los puntos del arreglo en forma de cuadrilátero.
Acá se ilustra en la figura 2.
Demostrar que la suma del n-ésimo número triangular con el n-ésimo menos uno número triangular es n elevado al cuadrado:
Tn + Tn-1= n2
Ya se ha demostrado que el número triangular n-ésimo está dado por:
Tn= ½ n (n+1)
Por lo tanto, el número triangular anterior es:
Tn-1 = ½ (n-1) ((n-1) + 1) = ½ n (n – 1)
La suma de ambos queda:
Tn + Tn-1 = ½ n (n+1) + ½ n (n – 1)
Se saca factor común ½ n para obtener:
Tn + Tn-1 = ½ n [ (n+1) + (n – 1) ] = ½ n [ n + 1 + n – 1]
Y de inmediato se simplifica la expresión en el interior de corchete:
Tn + Tn-1= ½ n [2 n] = ½ 2 n ⋅ n
Ahora, recordando que ½ por 2 es 1 y que n por n es n al cuadrado, se tiene:
Tn + Tn-1 = n2
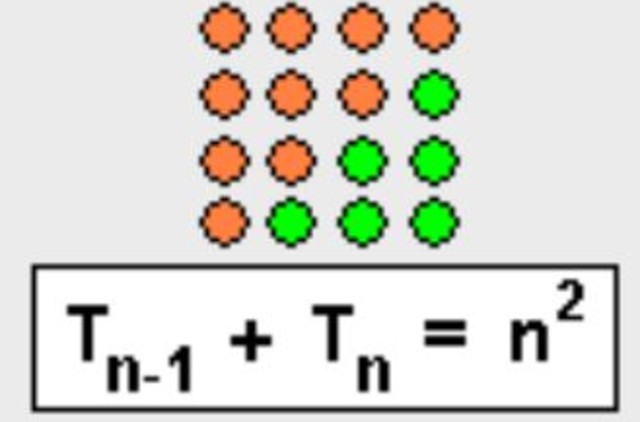
Esta propiedad también puede demostrarse en forma geométrica, simplemente se completa el triángulo para formar un cuadrado, tal como lo muestra la figura 3.
La diferencia del número triangular de orden n menos el número triangular de orden n-1 es n:
Tn – Tn-1 = n
Esto puede probarse simplemente recordando que el número triangular siguiente se obtiene del anterior mediante la fórmula:
Tn = Tn-1 + n
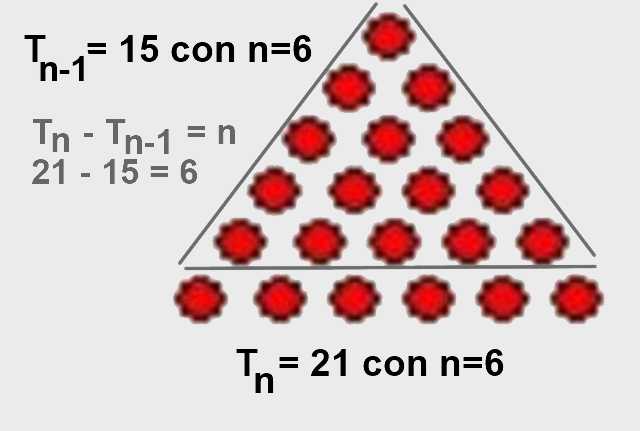
Y de allí resulta evidente que Tn – Tn-1 = n. También es fácil visualizarlo gráficamente, tal como se muestra en la figura 4.
La suma de los n primeros números triangulares Sn es igual a la sexta parte del producto de n multiplicado por (n + 1) y multiplicado por (n + 2):
Sn = ⅙ n (n + 1) (n + 2)
Hagamos uso del número triangular de orden n: Tn= ½ n (n+1). La suma de los primeros n números triangulares la denotaremos por Sn
Por ejemplo, S1significa la suma del primer número triangular, que sin duda será 1.
A continuación veamos si la fórmula que intentamos probar se cumple para n=1:
S1 = ⅙ 1⋅2⋅3 = 1
Efectivamente se comprueba la fórmula para n=1. Es fácil visualizar que la suma de n+1 primeros números triangulares será la suma de los n primeros más el próximo número triangular:
Sn+1 = Sn + Tn+1
Ahora supongamos que la fórmula de Sn se cumple para n, entonces la sustituimos en la expresión anterior y le agregamos el número triangular de orden n+1:
Sn+1 = [⅙ n (n + 1) (n + 2)] + [½ (n + 1) (n + 2)]
Veamos paso a paso lo que se obtiene:
-Efectuamos la suma de las dos expresiones fraccionales:
Sn+1 = [2 n (n + 1) (n + 2) + 6 (n + 1) (n + 2)] /12
-Se saca del numerador factor común a 2(n + 1) (n + 2) y se simplifica:
Sn+1 = 2 (n + 1) (n + 2) [n +3] / 12 = (n + 1) (n + 2) (n +3) / 6
El resultado anterior concuerda con la fórmula de Sn si se sustituye n por n+1, con lo cual ha quedado demostrada por inducción la fórmula de la suma de los primeros n términos triangulares.
Número tetraédrico
El resultado así obtenido se denomina número tetraédrico de orden n, porque es como ir acumulando capas triangulares que forman un tetraedro, tal como se muestra en la siguiente animación.

- Camacho J. Una aparición insospechada de los números triangulares. Recuperado de: masscience.com
- Claudio. Números triangulares. Recuperado de: simplemente numeros. blogspot. com
- Wikipedia. Número triangular. Recuperado de: es.wikipedia.com
- Wikipedia. Triangular number. Recuperado de: en.wikipedia.com
- Wikipedia. Tretrahedral number. Recuperado de: en.wikipedia.com
