Ley de Gauss: explicación, aplicaciones, ejercicios resueltos
¿Qué es la ley de Gauss?
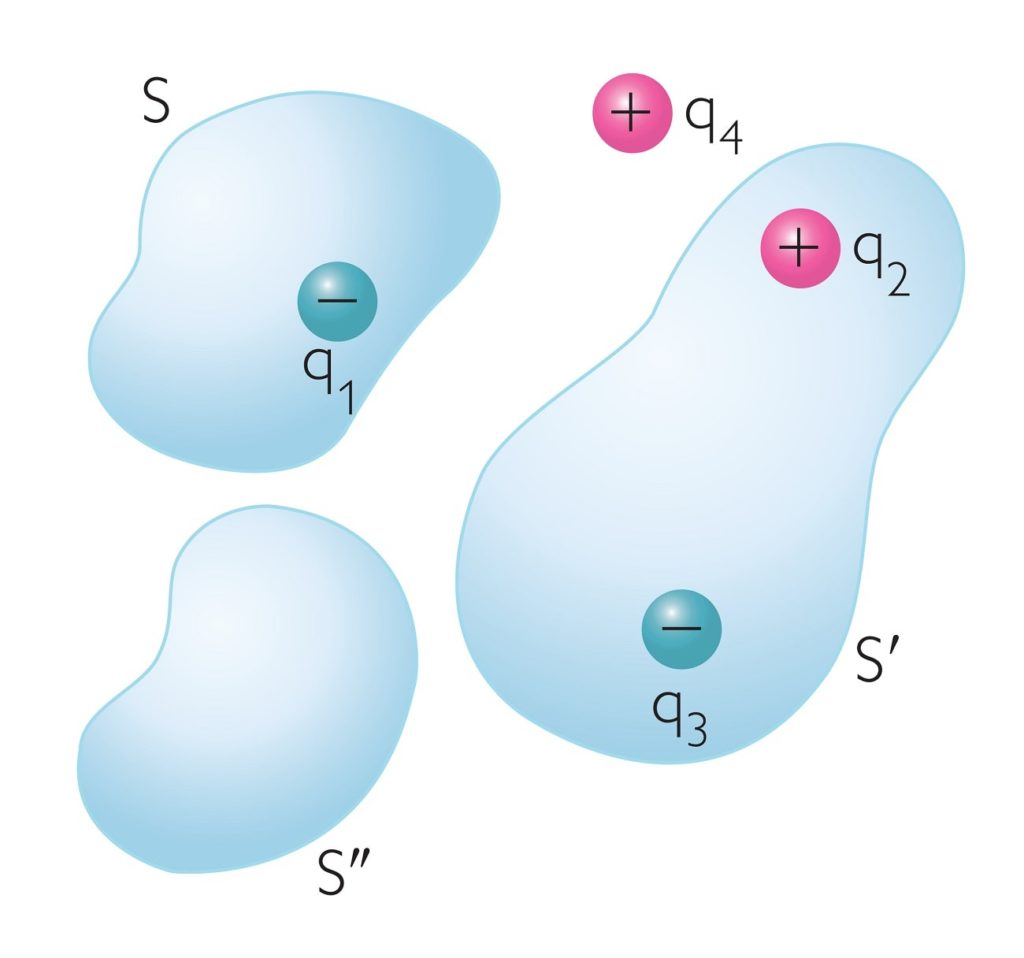
La ley de Gauss establece que el flujo de campo eléctrico, a través de una superficie cerrada imaginaria, es proporcional al valor neto de carga de las partículas encontradas en el interior de dicha superficie.
Denotando el flujo eléctrico a través de una superficie cerrada como ΦE y a la carga neta encerrada por la superficie por Qenc, entonces se establece la siguiente relación matemática:
ΦE = c ∙ Qenc
Donde c es la constante de proporcionalidad.
Explicación de la ley de Gauss
Para entender el significado de la ley de Gauss es necesario explicar los conceptos involucrados en su enunciado: carga eléctrica, campo eléctrico y flujo de campo eléctrico a través de una superficie.
Carga eléctrica
La carga eléctrica es una de las propiedades fundamentales de la materia. Un objeto cargado puede tener uno de los dos tipos de carga: positiva o negativa, aunque normalmente los objetos son neutros, es decir, tienen igual cantidad de carga negativa que positiva.
Dos objetos cargados con carga del mismo tipo se repelen aun cuando entre ellos no exista contacto y se encuentren en el vacío. Por el contrario, cuando cada uno de los cuerpos tienen cargas de diferente signo, entonces se atraen. Este tipo de interacción a distancia se conoce como interacción eléctrica.
En el sistema internacional de unidades SI la carga eléctrica se mide en culombios (C). El portador de carga elemental negativa es el electrón con carga de -1,6 x 10-19C y el portador de carga elemental positiva es el protón con un valor de carga +1,6 x 10-19C. Típicamente los cuerpos cargados tienen entre 10-9C y 10-3C.
Campo eléctrico
Un cuerpo cargado eléctricamente altera el espacio en su entorno, llenándolo de algo invisible llamado campo eléctrico. Para saber que ese campo está presente se requiere de una carga positiva puntual de prueba.
Si la carga de prueba se coloca en un lugar donde hay campo eléctrico, aparece sobre esta una fuerza en cierta dirección, que es la misma que la del campo eléctrico. La intensidad del campo es la fuerza sobre la carga de prueba dividida entre la cantidad de carga de la misma. Luego, las unidades del campo eléctrico E en el Sistema Internacional de unidades son newton entre coulomb: [E] = N/C.
Las cargas puntuales positivas producen un campo radial hacia afuera, mientras que las cargas negativas producen un campo dirigido radialmente hacia adentro. Además, el campo producido por una carga puntual decae con el inverso del cuadrado de la distancia a dicha carga.
Líneas de campo eléctrico
Michael Faraday (1791 – 1867) fue el primero en tener una imagen mental del campo eléctrico, imaginándolo como líneas que siguen la dirección del campo. En el caso de una carga puntual positiva dichas líneas son radiales partiendo desde centro hacia afuera. Donde las líneas están más juntas el campo es más intenso y menos intenso donde están más separadas.
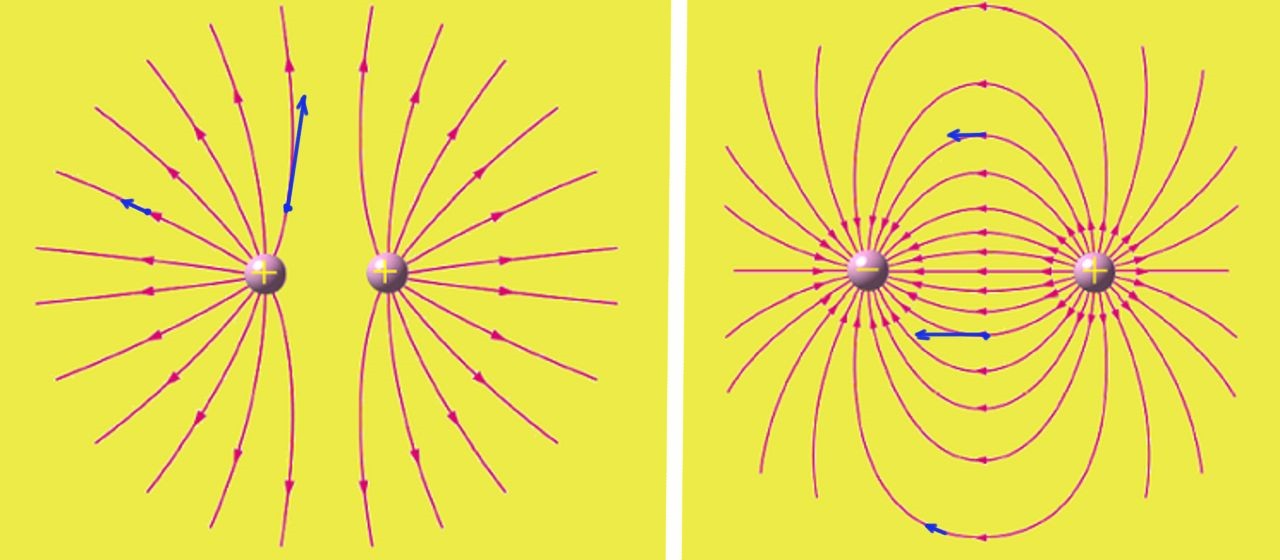
Las cargas positivas son las fuentes desde donde emergen las líneas de campo eléctrico, mientras que las cargas negativas son los sumideros de las líneas.
Las líneas de campo eléctrico no se cierran sobre sí mismas. En un conjunto de cargas las líneas salen de las cargas positivas y entran a las positivas, pero también pueden llegar o venir del infinito.
Tampoco se cruzan y en cada punto del espacio el vector campo eléctrico es tangente a la línea de campo y proporcional a la densidad de líneas allí.

Flujo de campo eléctrico
Las líneas de campo eléctrico se asemejan a las líneas de corriente de un río que fluye suavemente, de acá nace el concepto de flujo de campo eléctrico.
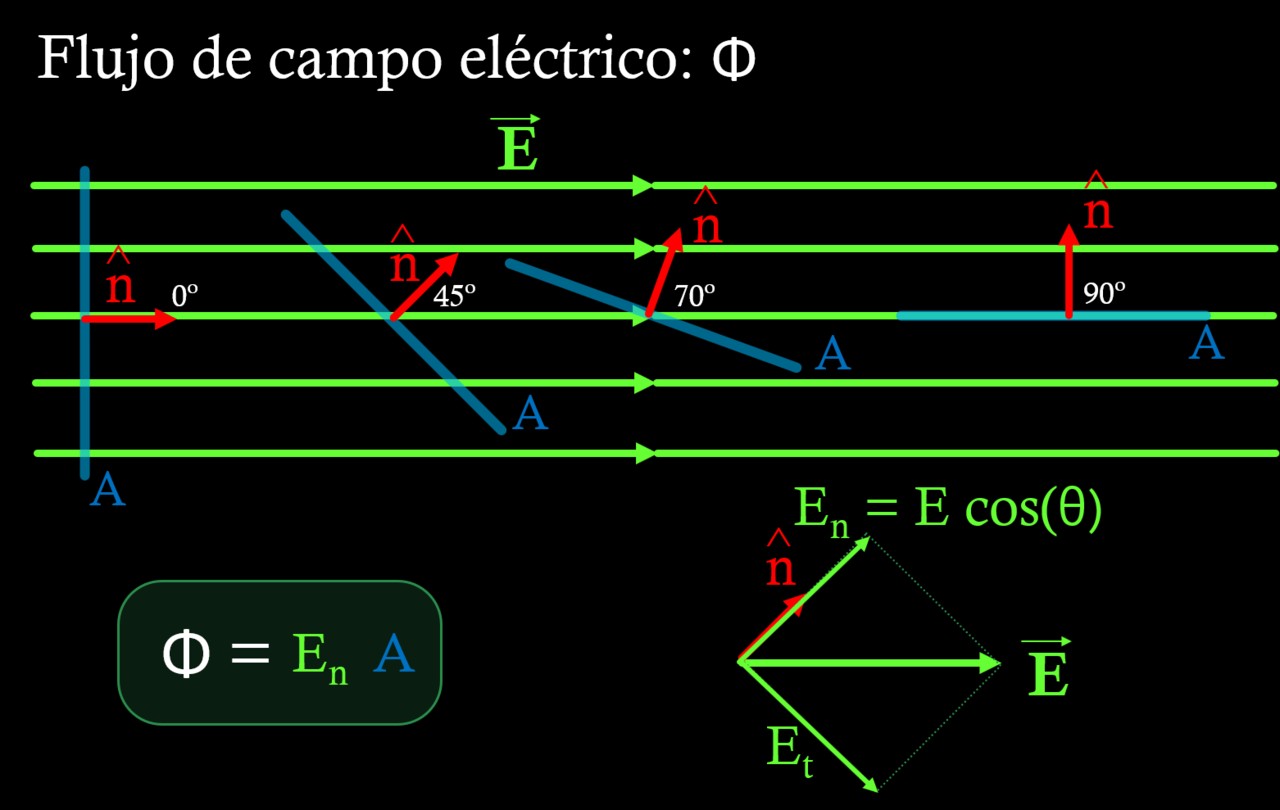
En una región donde el campo eléctrico es uniforme, el flujo Φ a través de una superficie plana es el producto de la componente normal del campo En a dicha superficie, multiplicada por el área A de la misma:
Φ = En ∙ A
La componente En se obtiene multiplicando la magnitud del campo eléctrico por el coseno del ángulo formado entre el campo y el vector normal unitario a la superficie de área A. (ver figura 4).
Aplicaciones de la ley de Gauss
La ley de Gauss puede aplicarse para determinar el campo eléctrico producido por distribuciones de carga con un alto grado de simetría.
Campo eléctrico de una carga puntual
Una carga puntual produce un campo eléctrico radial que es saliente si la carga es positiva y entrante en caso contrario.
Eligiendo como superficie gaussiana una esfera imaginaria de radio R y concéntrica a la carga Q, en todos los puntos de la superficie de dicha esfera el campo eléctrico es de igual magnitud y su dirección siempre es normal a la superficie. Entonces, en este caso el flujo de campo eléctrico es el producto de la magnitud del campo por el área total de la superficie esférica:
Φ = E ∙ A = E ∙ 4πR2
Por otra parte, la ley de Gauss establece que: Φ = c ∙ Q, siendo la constante de proporcionalidad c. Cuando se trabaja en unidades del sistema internacional de medidas, la constante c es el inverso de la permitividad del vacío, y la ley de Gauss se formula así:
Φ = (1/εo) ∙ Q
Incorporando el resultado obtenido para el flujo a la ley de Gauss se tiene:
E ∙ 4πR2 = (1/εo) ∙ Q
Y para la magnitud de E resulta:
E = (1/4πεo) ∙ (Q/ R2)
Que coincide plenamente con la ley de Coulomb del campo eléctrico de una carga puntual.
Ejercicios
Ejercicio 1
Dos cargas puntuales se encuentran dentro de una superficie gaussiana S de forma arbitraria. Se sabe que una de ellas tiene un valor de +3 nC (3 nano-coulomb). Si el flujo neto de campo eléctrico a través de la superficie gaussiana es de 113 (N/C) m2, ¿Cuál será el valor de la otra carga?
Solución
La ley de Gauss establece que
ΦE = (1/εo) ∙ Qenc
De allí la carga neta encerrada es:
Qenc = ΦE ∙ εo
Sustituyendo los datos resulta:
Qenc = 113 (N/C) m2 ∙ 8,85 x 10-12 (C2 m-2 N-1) = 1 x 10-9 C = 1 nC.
Pero Qenc = +Q – q, donde la carga positiva tiene un valor conocido de +3 nC, por lo tanto, la carga será necesariamente de -2 nC.
Ejercicio 2
En la figura 2 hay un arreglo (a la izquierda) de dos cargas positivas, cada una con valor +q y otro arreglo (a la derecha) con una carga +q y la otra -q. Cada arreglo está encerrado en una caja imaginaria con todas sus aristas de 10 cm. Si |q|= 3 μC, hallar el flujo neto de campo eléctrico a través de la caja para cada arreglo.
Solución
En el primer arreglo el flujo neto es:
ΦE = (1/εo) ∙ (+q + q) = 678000 (N/C) m2
En el arreglo de la derecha el flujo neto a través de la caja imaginaria que contiene al par de cargas es nulo.
Referencias
- Cosenza, M. Electromagnetismo. Universidad de los Andes.
- Díaz, R. Electrodinámica: notas de clase. Universidad Nacional de Colombia.
- Figueroa, D. (2005). Serie: Física para Ciencias e Ingeniería. Volumen 6. Electromagnetismo. Editado por Douglas Figueroa (USB).
- Jackson, J. D. Classical Electrodynamics. 3rd. Ed. Wiley.
- Tarazona, C. Introducción a la Electrodinámica. Editorial Universidad Manuela Beltrán.
