Escalas termométricas: concepto, fórmulas, ejemplos, ejercicios

¿Qué son las escalas termométricas?

Las escalas termométricas son aquellas que se usan en la medición de la temperatura, una magnitud escalar que sirve para cuantificar la energía térmica de un sistema. El dispositivo usado para medir temperatura, es decir, un termómetro, debe incorporar una escala para poder realizar la lectura.

Para construir una escala apropiada, hay que tomar dos puntos de referencia y dividir el intervalo entre ellos. Estas divisiones reciben el nombre de grados. De esta forma se compara la temperatura del objeto que se quiere medir, que puede ser la temperatura del café, del baño o la temperatura corporal, con la referencia marcada en el instrumento.

Las escalas de temperatura más utilizadas son las escalas Celsius, Fahrenheit, Kelvin y Rankine. Todas son igualmente apropiadas para medir la temperatura, ya que los puntos seleccionados como referencia son arbitrarios.

Tanto en la escala Celsius como en la escala Fahrenheit el cero de la escala no indica la ausencia de temperatura. Por tal motivo son escalas relativas. En cambio, para la escala Kelvin y la escala Rankine, el 0 representa el cese de la actividad molecular, de allí que sean consideradas escalas absolutas.

Escala celsius

Esta escala fue inventada por el astrónomo sueco del siglo XVIII Anders C. Celsius (1701–1744), cerca de 1735. Muy intuitiva, esta escala utiliza el punto de congelación y el punto de ebullición del agua a presión atmosférica normal (1 atm) como puntos de referencia.

El agua es una sustancia universal muy apropiada para esto, y sus valores son fáciles de obtener en el laboratorio.

En la escala Celsius el punto de congelación del agua es el que corresponde a 0 ° C y el punto de ebullición a 100 ° C, aunque originalmente Celsius los había propuesto a la inversa y más tarde se invirtió el orden. Entre estos dos valores de referencia hay 100 divisiones idénticas, por esto a veces se la conoce como escala centígrada.

Equivalencias

Para establecer una equivalencia entre los grados Celsius y otras escalas de temperatura, hay que tomar en cuenta dos aspectos:

• La relación entre la escala Celsius y la otra escala es lineal, por lo tanto es de la forma:

y = m.x +b

-Hay que conocer los puntos de referencia de ambas escalas.

Ejemplo: equivalencia entre las escalas Celsius y Fahrenheit

Sea T_ºC la temperatura en escala Celsius y T_ºF la temperatura en la escala Fahrenheit, por lo tanto:

T_ºC = m. T_ºF + b

Se sabe que 0 ºC = 32 ºF y 100 ºC = 212 ºF. Sustituimos estos valores en la ecuación anterior y obtenemos:

0 = 32m + b

100 = 212m + b

Este es un sistema de dos ecuaciones lineales con dos incógnitas, que se puede resolver por cualquiera de los métodos conocidos. Por ejemplo, mediante reducción:

100 = 212m + b

0 = -32m – b

________________

100 = 180m

m = 100 /180 = 5/9

Conociendo m, obtenemos b por sustitución:

b = -32m = -32. (5/9) = -160/9

Ahora sustituimos los valores de m y b en nuestra ecuación de equivalencia para obtener:

T_ºC = (5/9). T_ºF – (160/9)= (5T_ºF -160)/9

Equivalentemente: T_ºC = (5/9). (T_ºF – 32)

Esta ecuación permite pasar grados Fahrenheit a grados Celsius directamente, con solo escribir el valor en donde aparece T_ºF.

Ejemplo: equivalencia entre las escalas Celsius y Kelvin

Se han realizado muchos experimentos para intentar medir el cero absoluto de temperatura, es decir el valor para el cual desaparece toda actividad molecular en un gas. Esta temperatura se encuentra cerca de -273 ºC.

Sea T_K la temperatura en kelvin –no se utiliza la palabra “grado” para esta escala-, la equivalencia es:

T_ºC = T_K – 273

Es decir, las escalas se diferencian en que la escala Kelvin no tiene valores negativos. En la relación Celsius – Fahrenheit, la pendiente de la recta vale 5/9 y en este caso vale 1.

Los kelvins y los grados centígrados tienen el mismo tamaño, solo que la escala Kelvin, tal como se desprende de lo anterior, no contempla valores negativos de temperatura.

Escala Fahrenheit

Daniel Fahrenheit (1686–1736) fue un físico de origen alemán nacido en Polonia. Cerca de 1715, Fahrenheit fabricó un termómetro con una escala basada en dos puntos de referencia elegidos arbitrariamente. Desde entonces se usa mucho en los países de habla inglesa.

Originalmente Fahrenheit escogió la temperatura de una mezcla de hielo y sal para el punto de referencia inferior y la estableció como 0 °. Para el otro punto seleccionó la temperatura del cuerpo humano y la fijó en 100 grados.

Como era de esperar, tuvo algunos problemas para determinar cuál es la temperatura corporal “normal”, porque esta cambia a lo largo del día, o de un día para otro sin que la persona esté necesariamente enferma.

Resulta que hay personas totalmente sanas con temperatura corporal de 99.1 ºF, mientras que para otras lo normal es tener 98.6 ºF. Este último es el valor promedio para la población en general.

Así que los puntos de referencia de la escala Fahrenheit tuvieron que cambiar para el punto de congelación del agua, que se estableció en 32 ºF y el de ebullición en 212 ºF. Finalmente, la escala se dividió en 180 intervalos iguales.

Convertir grados Fahrenheit a grados Celsius

De la ecuación mostrada con anterioridad, se sigue que:

T_ºF = (9/5) T_ºC + 32

De igual forma podemos considerarlo así: la escala Celsius tiene 100 grados, mientras que la escala Fahrenheit tiene 180 grados. Entonces, por cada aumento o disminución de 1 ºC, se tiene un aumento o una disminución de 1.8 ºF = (9/5) ºF

Ejemplo

Mediante las ecuaciones anteriores, encontrar una fórmula que permita pasar de grados Fahrenheit a escala Kelvin:

Sabiendo que: T_ºC = T_K – 273 y sustituyendo en la ecuación ya deducida, se tiene:

T_ºC = T_K – 273

Por lo tanto: T_ºF = (9/5)(T_K – 273) + 32 = (9/5) T_K – 459.4

Escala Kelvin

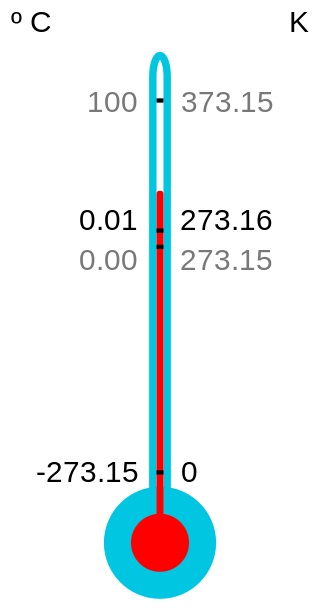
William Thomson (1824–1907), Lord Kelvin, propuso una escala sin puntos de referencia arbitrarios. Esta es la escala de temperatura absoluta que lleva su nombre, propuesta en 1892. No tiene valores de temperatura negativos, ya que el 0 absoluto es la temperatura más baja posible.

A la temperatura de 0 K cualquier movimiento de las moléculas ha cesado completamente. Esta es la escala del Sistema Internacional (SI), aunque la escala Celsius es considerada también como unidad accesoria. Recordemos que la escala Kelvin no utiliza “grados”, por eso una temperatura cualquiera se expresa como el valor numérico más la unidad, llamada “kelvin”.

Hasta ahora no se ha podido alcanzar el cero absoluto, pero los científicos se han acercado bastante.

En efecto, en los laboratorios especializados en bajas temperaturas, han conseguido enfriar muestras de sodio a 700 nanokelvin o 700 x 1010^-9 kelvin. Por otra parte, hacia el otro extremo de la escala, se sabe que una explosión nuclear puede generar temperaturas de 100 o más millones de kelvin.

Cada kelvin corresponde a 1/273.16 partes de la temperatura del punto triple del agua. A esta temperatura se encuentran en equilibrio las tres fases del agua.

Escala Kelvin y escalas Celsius y Fahrenheit

La relación entre las escalas Kelvin y Celsius es –redondeando 273.16 a 273-:

T_K = T_ºC + 273

Del mismo modo, por sustitución se obtiene una relación entre las escalas Kelvin y Fahrenheit:

T_K =5(T_ºF + 459.4)/9

Escala Rankine

La escala Rankine fue propuesta por William Rankine, ingeniero nacido en Escocia (1820-1872). Pionero de la Revolución Industrial, realizó grandes aportes a la termodinámica. En 1859 propuso una escala de temperatura absoluta, fijando el cero a −459,67 °F.

En esta escala el tamaño de los grados es el mismo que en la escala Fahrenheit. La escala Rankine se denota como R y al igual que con la escala Kelvin, sus valores no se denominan grados, sino rankine.

De esta forma:

0 K = 0 R = −459,67 °F = – 273.15 ºC

Resumiendo, aquí están las conversiones necesarias para ir a la escala Rankine desde cualquiera de las ya descritas:

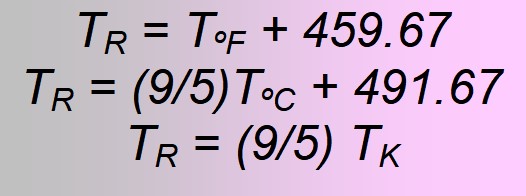
Escala Réaumur

Otra escala de temperaturas empleada con anterioridad es la escala Réaumur, a la que sí se denota como grados o ºR. Actualmente está en desuso, aunque se usaba mucho en Europa hasta que fue desplazada por la escala Celsius.

Fue creada por René-Antoine Ferchault de Réaumur (1683-1757) hacia 1731. Sus referencias son: 0 °R para el punto de congelación del agua y 80 °R para el punto de ebullición.

Como se observa, coincide con la escala Celsius en el cero, pero desde luego no en los demás valores. Se relaciona con la escala centígrada mediante:

T_ºR=(4/5) T_ºC

Además se tienen otras equivalencias:

T_ºR= (4/5) (T_K – 273) = ( 4/9)(T_ºF-32)= (4/5)(5.T_R/9 –  273) = (4/9)T_R – 218.4

Ejercicios resueltos

Ejercicio 1

Encontrar el valor numérico en el que la escala centígrada coincide con la escala Fahrenheit.

Solución

Tal como hemos visto en los apartados anteriores, estas escalas no coinciden, ya que los puntos de referencia son diferentes; sin embargo es posible encontrar un valor x, tal que represente la misma temperatura en ambas escalas. Por lo tanto se toma la ecuación:

T_ºC = (5/9). T_ºF – (160/9)= (5T_ºF -160)/9

Y puesto que las temperaturas deben coincidir, entonces T_ºC  = T_ºF = x, se sigue que:

x = (5x – 160)/9

9x = 5x -160

4x = -160

x = – 40

Cuando T_ºC  = -40 ºC, también T_ºF = -40 ºF

Ejercicio2

El vapor que sale de una caldera se encuentra a una temperatura de 610 ºR. Encontrar la temperatura en grados Fahrenheit y en grados Celsius.

Solución

Se utilizan las equivalencias encontradas en la sección de la escala Réaumur, por lo tanto: T_ºC=(5/4) T_ºR =(5/4). 610 º C = 762.5 ºC.

Enseguida se puede convertir este valor encontrado para pasar a grados Fahrenheit, o emplear otra de las conversiones mencionadas:

T_ºF = (9/5) T_ºC + 32= (9/5) 762.5  + 32 ºC = 1404.5 ºF

O bien esta otra, que da el mismo resultado: T_ºR =( 4/9)(T_ºF – 32)

Se despeja: T_ºF =( 9/4) T_ºR + 32 =( 9/4) 610 + 32 ºF= 1404.5 ºF.

Resumen de conversiones

En resumen, el siguiente cuadro facilita las conversiones para todas las escalas descritas:

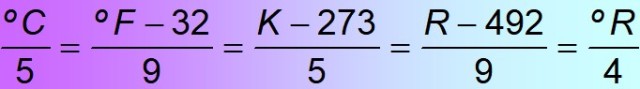
Referencias

1. Escalas de Temperatura. Recuperado de: thales.cica.es.
2. Knight, R.  2017. Physics for Scientists and Engineering: a Strategy Approach. Pearson.
3. Tillery, B. 2012. Physical Science. McGraw Hill.
4. Wikipedia. Grado Celsius. Recuperado de: es.wikipedia.org
5. Wikipedia. Grado Fahrenheit. Recuperado de: es.wikipedia.org.
6. Wikipedia. Rankine. Recuperado de: es.wikipedia.org.