Fracciones: tipos, ejemplos, ejercicios resueltos
Las fracciones o números fraccionarios son aquellos números que se representan indicando el cociente entre dos números enteros a y b, siempre y cuando b sea diferente de 0. Por ejemplo, 1/3 es una fracción que se lee como “un tercio”.
Al número a se le conoce como numerador de la fracción y al b como denominador de la misma. El denominador nos indica en cuántas partes hay que dividir el todo. Por su parte, el numerador señala cuántas partes de ese todo se tomaron.

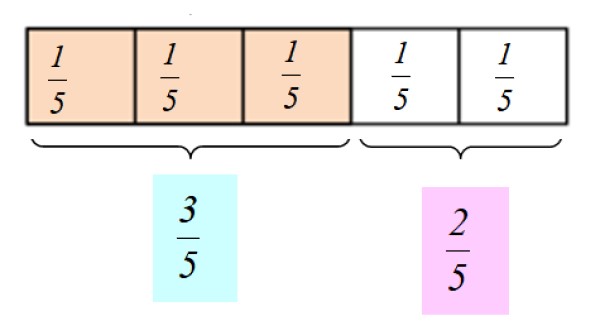
El todo es cualquier cosa que se quiera dividir o fraccionar, por ejemplo una pizza o la barra de chocolate que se muestra en la figura 1. La barra está confeccionada de tal forma que es muy fácil dividirla en 5 partes iguales, donde cada parte equivale a 1/5 de la barra completa.
En la fracción o número fraccionario 1/5, el numerador vale 1 y el denominador vale 5. La fracción se lee “un quinto”.
Supongamos que nos comemos 3 pedazos de chocolate. Diríamos que nos hemos comido 3/5 partes de la barra y quedan 2/5 partes para compartir con un amigo. También podemos decir que nos comimos “tres quintos del chocolate” y obsequiamos “dos quintos” al amigo.
La representación gráfica de estos números fraccionarios es la siguiente:
Índice del artículo
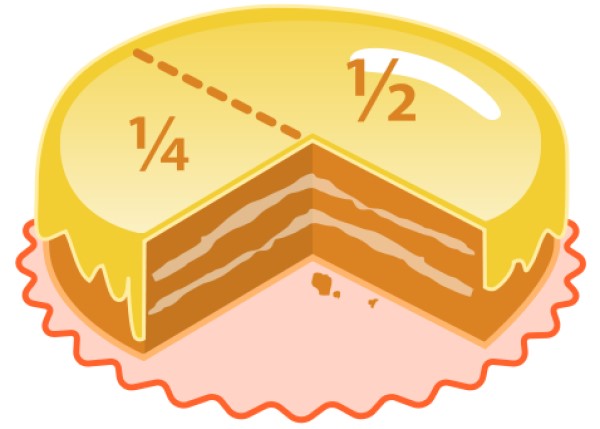
Una fracción es propia cuando el numerador es menor que el denominador y de esta forma su valor es menor que 1. Las fracciones del apartado anterior, en el ejemplo del chocolate, son fracciones propias.
Otros ejemplos de fracciones propias son: ½ ; 8/10 ; 3/4 y más.
El numerador de las fracciones impropias es mayor que el numerador. Por ejemplo 4/3, 8/5, 21/10 pertenecen a esta categoría.
Estas fracciones representan un número entero. Entre ellas están 4/2, 10/5 y 27/3, ya que si nos fijamos bien, el resultado de dividir numerador entre denominador de estas fracciones da un número entero.
Así: 4/2 =2, 10/5 = 2 y 27/3 = 9.
Dos fracciones n/m y p/q son equivalentes cuando al dividir numerador entre denominador se obtiene la misma cantidad. De esta forma las fracciones equivalentes representan la misma parte del todo.
Como ejemplo tenemos las fracciones: 15/2 y 30/4. Al dividir 15 entre 2 se obtiene 7.5, pero también es igual si se divide 30 entre 4.
Para saber si dos fracciones n/m y p/q son equivalentes, se verifica el cumplimiento de la siguiente igualdad:
n*q = m.p
Cuando el numerador y el denominador se dividen ambos por la misma cifra y con tal de que el resultado sea entero, se obtiene una fracción equivalente a la original, pero con números más pequeños.
Este proceso continúa mientras el numerador y el denominador tengan el mismo divisor exacto. Cuando no es posible seguir dividiendo es que se llegó a la fracción irreducible de la fracción original.
La ventaja que tiene trabajar con la fracción irreducible es que se obtiene una fracción equivalente pero con números más pequeños. Por eso cuando se trabaja con fracciones, hay que asegurarse de reducirlas siempre que sea posible, para facilitar los cálculos.
Supongamos la fracción 12/20, siendo numerador y denominador pares, se pueden dividir ambos entre 2:
12/20 = 6/10
Y una vez más:
6/10 = 3/5
La fracción 3/5 es equivalente a 12/20, pero más sencilla.
Una fracción impropia también admite representación como un número mixto, llamado así porque tiene una parte entera y otra parte fraccionaria, siendo la parte fraccionaria una fracción propia.
Veamos un ejemplo rápido con la fracción 15/2 que sabemos que equivale a 7.5.
Podemos expresar a 15/2 como número mixto así:
15/2 = 7 + 0.5
Pero 0.5 = ½. Por lo tanto 15/2 = 7 ½ que se lee “siete y un medio”.
Los números fraccionarios son necesarios porque tanto los naturales como los enteros son insuficientes cuando queremos dividir cosas como la barra de chocolate.
Y por eso existe una infinita variedad de patrones de medida y objetos cuyas especificaciones incluyen números fraccionarios, por no hablar de la cantidad de situaciones cotidianas en las que estos son necesarios.
En los países donde se usa el sistema métrico decimal es común el uso del kilo para referirse al peso de muchos alimentos. No siempre queremos comprar cantidades enteras, sino un poco más o un poco menos.
Por eso pedimos:
- ½ kg de pescado
- ¾ kg de tomates
- ¼ kilo de cebolla
- 1 ½ kg de duraznos (1 Kilo y medio).
Y al usar los patrones de medida anglosajones ocurre igual: necesitamos 2 libras y media o 1/4 de libra de alguna cosa.
Todos estos números son fraccionarios y, como hemos visto, corresponden a dos tipos diferentes de fracciones: propias e impropias.
Las recetas de cocina con frecuencia hacen uso de los números fraccionarios para indicar la cantidad de ciertos ingredientes. Por ejemplo:
- ½ taza de harina
- ¾ kg de azúcar para preparar una torta.
Dimensiones de mobiliario, piezas textiles y toda clase de utensilios domésticos se miden en fracciones de metro o de pulgada, tanto si se usa el sistema métrico decimal de medidas o el anglosajón.
Aún en países donde impera el sistema métrico decimal, las tuberías comerciales de cobre, acero y otros materiales para la plomería suelen venir con diámetros especificados en pulgadas. Igualmente otras piezas de ferretería como tornillos y tuercas.
Como una pulgada es equivalente a 2.54 cm, usualmente estas piezas, que tienen diámetros menores, se expresan en fracciones de pulgada.
Medidas muy habituales para las tuberías domésticas son:
- ½ pulgada
- ¼ de pulgada
- 3/8 y 5/8 de pulgada.
Cotidianamente se emplean los números fraccionarios para expresar intervalos de tiempo tales como ¼, ½ y ¾ de hora, o incluso un poco mayores: 1 hora y ¼ y así sucesivamente.

Hoy, Juanito ha llevado al colegio una tarta por su cumpleaños y quiere repartirla entre todos sus amigos, pero a la profesora le quiere dar un trozo que sea tres veces más grande respecto al de los niños.
Teniendo en cuenta que hay 24 niños + la profesora, a la cual le quiere dar el equivalente a tres trozos, ¿En cuántos trozos debería cortar la tarta?
Solución
Si Juanito quisiera solo repartir la tarta entre sus amigos, a cada uno le correspondería 1/24.
Pero, como quiere darle una parte a la profesora y que el trozo sea tres veces más grande, tendría que repartir la tarta entre 24 alumnos + 3 trozos para la profesora. Es decir, a cada niño le corresponde 1/27 trozos y a la profesora 3/27 trozos.
Además, si reducimos la fracción 3/27 obtenemos que la profesora se llevara 1/9 parte de la tarta.
Una empresa con un jefe y tres empleados tiene 6000€ de ingresos todos los meses. ¿Cuánto dinero le corresponde a cada persona si el jefe quiere quedarse con la mitad de lo ganado?
Solución
Si el jefe quiere ganar la mitad, deberá quedarse con 6000/2, lo que hacen 3000€. De los otros 3000€ restantes es lo que se deberán repartir los tres empleados. Así pues, cada empleado ganará 3000/3, dando como resultado 1000€.
Hallar la fracción irreducible de:
a) 12 / 18 y b) 4/11
Solución a
En el primer caso notamos que tanto el numerador como el denominador son pares y divisibles entre 2. También son divisibles entre 3, ya que 12 y 18 son múltiplos de esa cifra.
Así que podemos simplificar la fracción dividiendo tanto el numerador como el denominador ya sea entre 2 o entre 3, el orden es indiferente.
Comenzando por dividir entre 2:
12/18 = 6/9
Ahora notamos que tanto el numerador como el denominador de esta fracción equivalente son múltiplos de 3, así que dividiendo ambos entre esta cifra:
6/9 = 2/3
Y puesto que 2 y 3 son números primos, ya no tienen ningún otro divisor común salvo 1. Hemos llegado a la fracción irreducible.
También se pudo haber calculado el máximo común divisor MCD del numerador y el denominador. Para 12 y 18:
MCD (12,18) = 6.
Y luego se divide numerador y denominador por este número, lo cual es equivalente a hacerlo por etapas.
Solución b
Aquí observamos que 11 es un número primo y sus divisores son 1 y 11. Por su parte el 4 admite como divisores al 4, al 2 y al 1. Excepto el 1, estos números no tienen un divisor común y por lo tanto la fracción 4/11 es irreducible.
Indicar cuál es la fracción mayor de cada par:
a) ¾ y 5/4
b) 3/7 y 4/9
Solución a
Cuando dos fracciones positivas tienen igual denominador, la mayor es aquella que tiene el numerador más grande. Por lo tanto 5/4 es mayor, ya que 5 > 3.
Solución b
Si las fracciones n/m y p/q tienen distinto denominador y ambas son positivas, el criterio de comparación es el siguiente:
Si n.q > m. p, entonces n/m > p/q
Otra opción es encontrar la expresión decimal de cada fracción y comparar.
De acuerdo al primer criterio: n = 3, m= 7, p = 4, q = 9. Por lo tanto: n.q = 3*4 = 12 y m.p = 7*4 = 28.
Como 12 28, ocurre que 3/7 4/9.
O expresamos cada fracción como decimal, obteniendo esto:
3/7 = 0.428571428….
4/9 = 0.444444444….
Los puntos suspensivos indican que la cantidad de decimales es infinita. Pero esto basta para comprobar que en efecto, 4/9 > 3/7.
- Baldor, A. 1986. Aritmética. Ediciones y Distribuciones Códice.
- Carena, M. 2019. Manual de Matemática. Universidad Nacional del Litoral.
- Figuera, J. 2000. Matemática 8. Ediciones Co-Bo.
- Jiménez, R. 2008. Álgebra. Prentice Hall.
- The Math Page. What is a fraction? Recuperado de: themathpage.com.
