Vectores colineales: concepto, sistema y ejemplos

¿Qué son los vectores colineales?

Los vectores colineales son uno de los tres tipos de vectores existentes. Se trata de aquellos vectores que se encuentran en la misma dirección o línea de acción. Esto quiere decir lo siguiente: dos o más vectores serán colineales si se da el caso de que se encuentran dispuestos en rectas que son paralelas entre sí.

Un vector se define como una magnitud aplicada a un cuerpo y se caracteriza por tener una dirección, un sentido y una escala. Los vectores se pueden encontrar en el plano o en el espacio y pueden ser de distintos tipos: vectores colineales, vectores concurrentes y vectores paralelos.

¿Cuándo hay vectores colineales?

Los vectores son colineales si la línea de acción de uno es exactamente la misma línea de acción de todos los demás vectores, sin importar el tamaño y sentido de cada uno de los vectores.

Los vectores son utilizados como representaciones en diferentes áreas como matemática, física, álgebra y también en geometría, donde los vectores son colineales solo cuando su dirección es la misma, sin importar que su sentido no lo sea.

Ejemplos de vectores colineales

• Dos o más vectores son colineales si la relación que existe entre las coordenadas es igual.

Ejemplo 1

Se tienen los vectores m={m_x; m_y} y n={n_x; n_y}. Estos son colineales si:

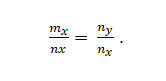
Ejemplo 2

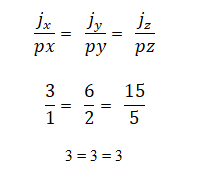
• Dos o más vectores son colineales si el producto o multiplicación vectorial es igual a cero (0). Esto es porque, en el sistema de coordenadas, cada vector es caracterizado por sus respectivas coordenadas, y si estas son proporcionales entre sí los vectores serán colineales. Esto es expresado de la siguiente manera:

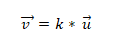
Ejemplo 1

Se tienen los vectores a=(10 , 5) y b=(6 , 3). Para determinar si son colineales se aplica la teoría del determinante, que establece la igualdad de los productos cruzados. De esa forma, se tiene que:

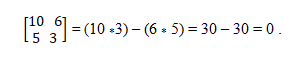
Sistema de vectores colineales

Los vectores colineales son representados gráficamente usando la dirección y el sentido de estos —teniendo en cuenta que estos deben pasar por el punto de aplicación— y el módulo, que es una escala o longitud determinada.

El sistema de vectores colineales es formado cuando sobre un objeto o cuerpo actúan dos o más vectores, que representan a una fuerza y que actúan en la misma dirección.

Por ejemplo, si se aplican dos fuerzas colineales sobre un cuerpo, la resultante de estas solo va a depender del sentido en el que actúen. Existen tres casos, que son:

Vectores colineales con sentidos contrarios

La resultante de dos vectores colineales es igual a la suma de estos:

R = ∑ F = F₁ + F_2.

Ejemplo

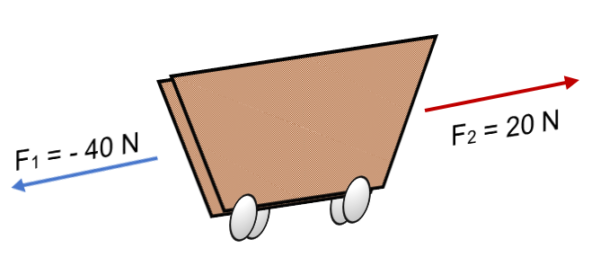
Si sobre un carrito actúan dos fuerzas F₁ = 40 N y F₂ = 20 N en sentido contrario (como se muestra en la imagen), la resultante es:

R = ∑ F = (- 40 N) + 20N.

R = – 20 N.

Vectores colineales con el mismo sentido

La magnitud de la fuerza resultante será igual a la suma de los vectores colineales:

R = ∑ F = F₁ + F_2.

Ejemplo

Si sobre un carrito actúan dos fuerzas F₁ = 35 N y F₂ = 55 N en el mismo sentido (como se muestra en la imagen), la resultante es:

R = ∑ F = 35 N + 55N.

R = 90 N.

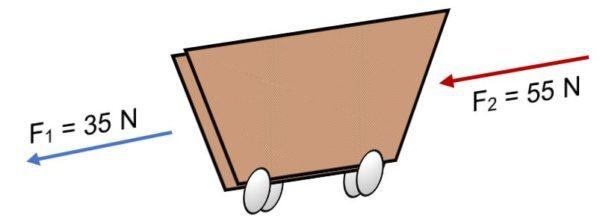
La resultante positiva indica que los vectores colineales actúan hacia la izquierda.

Vectores colineales con magnitudes iguales y sentidos contrarios

La resultante de los dos vectores colineales será igual a la suma de los vectores colineales:

R = ∑ F = F₁ + F_2.

Como las fuerzas tienen la misma magnitud pero en sentido contrario —es decir, que una será positiva y otra negativa—, al sumar las dos fuerzas la resultante será igual a cero.

Ejemplo

Si sobre un carrito actúan dos fuerzas F₁ = -7 N y F₂ = 7 N, que poseen la misma magnitud, pero en sentido contrario (como se muestra en la imagen), la resultante es:

R = ∑ F = (-7 N) + 7N.

R = 0.

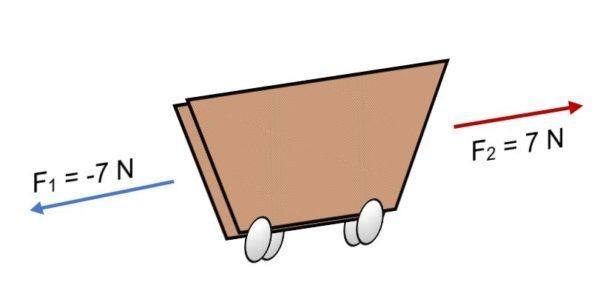
Como la resultante es igual a 0, significa que los vectores se equilibran entre sí y, por lo tanto, el cuerpo está en equilibrio o en reposo (no se moverá).

Diferencia entre vectores colineales y concurrentes

Los vectores colineales se caracterizan por tener la misma dirección en una misma recta, o porque son paralelos a una recta; es decir, son vectores directores de rectas paralelas.

Por su parte, los vectores concurrentes son definidos porque ellos se encuentran en diferentes líneas de acción que se interceptan en un único punto.

En otras palabras, ellos tienen un mismo punto de origen o llegada —independientemente de su módulo, sentido o dirección—, formando un ángulo entre ellos.

Los sistemas de vectores concurrentes son resueltos por métodos matemáticos o gráficos, que son el método del paralelogramo de fuerzas y método del polígono de fuerzas. A través de estos se determinará el valor de un vector resultante, que indica la dirección en la que un cuerpo se moverá.

Básicamente, la principal diferencia entre los vectores colineales y los concurrentes es la línea de acción en la que actúan: los colineales actúan en una misma línea, mientras que los concurrentes en diferentes.

Es decir, los vectores colineales actúan en un solo plano, “X” o “Y”; y los concurrentes actúan en ambos planos, partiendo desde un mismo punto.

Los vectores colineales no se encuentran en un punto, como lo hacen los concurrentes, porque ellos son paralelos entre sí.

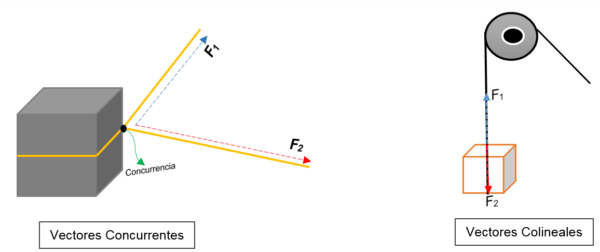
En la imagen izquierda puede verse un bloque. Es amarrado con una cuerda y el nudo la divide en dos; al ser halados hacia diferentes orientaciones y con diferentes fuerzas, el bloque se moverá hacia una misma dirección.

Se están representando dos vectores que concurren en un punto (el bloque), sin importar su módulo, sentido o dirección.

En cambio, en la imagen derecha aparece una polea que levanta una caja. La cuerda representa la línea de acción; cuando es halada, dos fuerzas (vectores) actúan sobre ella: una fuerza de tensión (al subir el bloque) y otra fuerza, la que ejerce el peso del bloque. Ambas poseen la misma dirección, pero en sentidos opuestos; no concurren en un punto.