Rectas oblicuas: características, ecuaciones y ejemplos
Las rectas oblicuas son aquellas que están inclinadas, ya sea respecto a una superficie plana o a otra recta que indique una dirección en particular. A modo de ejemplo considérense las tres rectas dibujadas en un plano que aparecen en la siguiente figura.
Conocemos sus respectivas posiciones relativas porque las comparamos con una línea de referencia, que usualmente es el eje x que denota la horizontal.
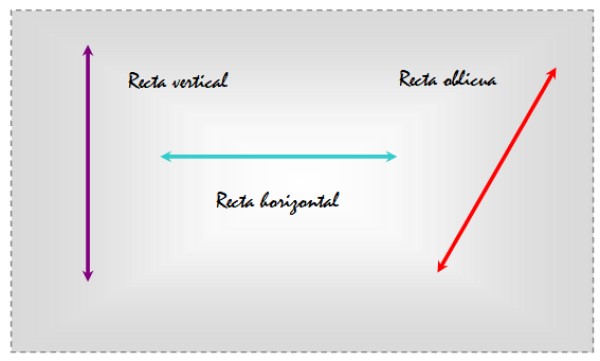
De esta manera, eligiendo como referencia la horizontal, la recta de la izquierda es vertical, la del centro es horizontal y la de la derecha es oblicua, ya que está inclinada respecto a las líneas cotidianas de referencia.
Ahora bien, las rectas que se encuentran sobre un mismo plano, como puede ser la superficie del papel o la pantalla, ocupan distintas posiciones relativas entre sí, dependiendo de si se intersectan o no. En el primer caso son rectas secantes, mientras que en el segundo, son paralelas.
Por otra parte las rectas secantes pueden ser a su vez rectas oblicuas o rectas perpendiculares. En ambos casos, las pendientes de las rectas son diferentes, pero las rectas oblicuas forman entre sí ángulos α y β, distintos de 90º, mientras que los ángulos determinados por las rectas perpendiculares siempre son de 90º.
En la siguiente figura se resumen estas definiciones:

Índice del artículo
Para conocer las posiciones relativas de las rectas en el plano, es necesario conocer el ángulo que forman entre sí. Nótese que las rectas son:
Paralelas: si tienen la misma pendiente (igual dirección) y nunca se intersectan, por ello sus puntos son equidistantes.
Coincidentes: cuando todos sus puntos coinciden y por lo tanto tienen la misma pendiente, pero la distancia entre sus puntos es nula.
Secantes: si sus pendientes son distintas, la distancia entre sus puntos varía y la intersección es un único punto.
Entonces, una manera de saber si dos rectas en el plano son secantes o paralelas es a través de su pendiente. Los criterios de paralelismo y perpendicularidad de las rectas son los siguientes:
Sean dos rectas L1 y L2 pertenecientes a un plano, cuyas pendientes son respectivamente m1 y m2. Dichas rectas son paralelas si m1 = m2 y son perpendiculares cuando m1=-1/m2
Si conociendo las pendientes de dos rectas en el plano no se cumple ninguno de los criterios anteriores, concluimos que las rectas son oblicuas. Conociendo dos puntos de una recta, la pendiente se calcula de inmediato, como veremos en la siguiente sección.
Se puede averiguar si dos rectas son secantes o paralelas encontrando su intersección, resolviendo el sistema de ecuaciones que forman: si hay solución son secantes, si no la hay son paralelas, pero si las soluciones son infinitas, las rectas son coincidentes.
Sin embargo este criterio no nos informa acerca del ángulo entre dichas rectas, aún en caso de que tengan intersección.
Para conocer el ángulo entre las rectas, se necesitan dos vectores u y v que pertenezcan a cada una de ellas. Así es posible saber el ángulo que forman mediante el producto escalar de los vectores, definido de esta forma:
u•v =u.v.cos α
Una recta en el plano cartesiano puede representarse de varias formas, como por ejemplo:
–Forma pendiente-intersección: si m es la pendiente de la recta y b es la intersección de la recta con el eje vertical, la ecuación de la recta es y = mx +b.
–Ecuación general de la recta: Ax + By +C = 0, donde m = A/B es la pendiente.
En el plano cartesiano, las rectas verticales y horizontales son casos particulares de la ecuación de la recta.
–Rectas verticales: x = a
–Rectas horizontales: y = k
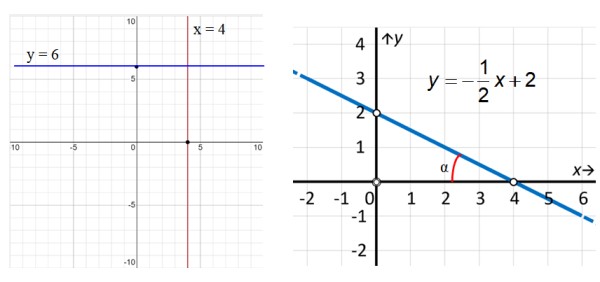
En los ejemplos de la figura 3, la recta de color rojo vertical tiene ecuación x=4, mientras que la recta paralela al eje x (azul) tiene ecuación y = 6. En cuanto a la recta de la derecha, vemos que es oblicua y para encontrar su ecuación usamos los puntos resaltados en la figura: (0,2) y (4,0) de esta forma:
m = (y2 – y1) / (x2 – x1) = (2 – 0) / (0 – 4) = – ½
El corte de esta recta con el eje vertical es y = 2, según se advierte de la gráfica. Con esta información:
y = (-½)x+2
Determinar el ángulo de inclinación respecto al eje x es sencillo. Note que:
α = arctg (2/4) = 26.6º
Por lo tanto el ángulo positivo desde el eje x hasta la recta es: 180º – 26.6º = 153.4º

Las rectas oblicuas aparecen en muchos lugares, es cuestión de prestar atención para encontrarlas en la arquitectura, el deporte, el cableado del suministro eléctrico, las tuberías y en muchos más lugares. En la naturaleza las rectas oblicuas también se hacen presentes, como veremos a continuación:
La luz del sol se propaga en línea recta, pero la forma redondeada de la Tierra afecta la manera en que la luz solar incide sobre la superficie.
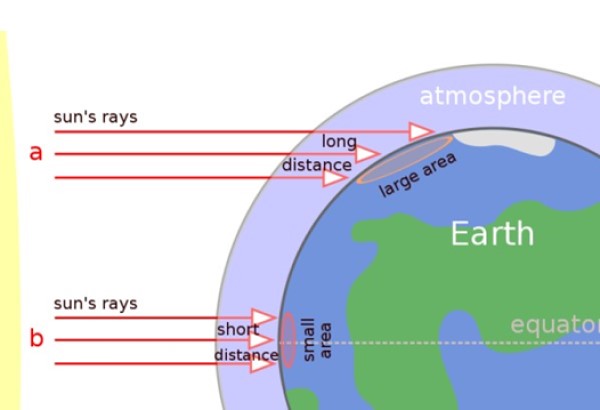
En la imagen de abajo podemos apreciar claramente que los rayos solares inciden perpendicularmente en las regiones tropicales, pero en cambio llegan oblicuamente a la superficie en las regiones templadas y en los polos.
Por ello los rayos del sol viajan una distancia más larga a través de la atmósfera y además el calor se esparce sobre una superficie mayor (ver figura). El resultado es que las zonas cercanas a los polos son más frías.
Cuando dos rectas no están en un mismo plano, aun así pueden ser oblicuas o alabeadas, como también se las conoce. En tal caso sus vectores directores no son paralelos, pero al no pertenecer a un mismo plano, dichas rectas no tienen intersección.
Por ejemplo, las rectas en la figura 6 derecha claramente están en planos distintos. Si se miran desde arriba se observa que efectivamente se cruzan, pero no tienen un punto en común. A la derecha vemos las ruedas de la bicicleta, cuyos rayos parecen cruzarse cuando se ven de frente.

- Geometría. Vector director de una recta. Recuperado de: juanbragado.es.
- Larson, R. 2006. Cálculo con Geometría Analítica. 8va. Edición. McGraw Hill.
- Las Matemáticas son un juego. Líneas y Ángulos. Recuperado de: juntadeandalucia.es.
- Rectas que se cruzan. Recuperado de: profesoraltuna.com.
- Villena, M. Geometría Analítica en R3. Recuperado de: dspace.espol.edu.ec.
