Números reales: historia, ejemplos, propiedades, operaciones
Los números reales constituyen el conjunto numérico que abarca a los números naturales, los enteros, los racionales y los irracionales. Se denotan con el símbolo ℝ o simplemente R y el alcance que tienen en ciencia, ingeniería y economía es tal, que al hablar de “número”, casi se da por sentado de que se trata de un número real.
Los números reales se vienen utilizando desde la antigüedad, si bien no se les daba ese nombre. Ya a partir de la época en que Pitágoras desarrolló su célebre teorema, surgieron números que no se podían obtener como cocientes de números naturales o números enteros.
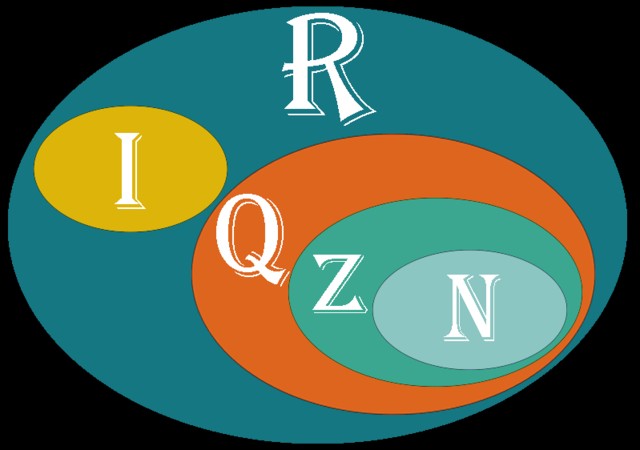
Ejemplos de números son √2, √3 y π. Estos números son llamados irracionales, en contraposición a los números racionales, que sí provienen de cocientes entre números enteros. Era necesario pues, un conjunto numérico que abarcase ambas clases de números.
El término “número real” fue creado por el gran matemático René Descartes (1596-1650), para distinguir entre las dos clases de raíces que pueden surgir de resolver una ecuación polinómica.
Algunas de estas raíces pueden ser raíces pares de números negativos, a estas Descartes las llamó “números imaginarios” y a las que no, eran números reales.
La denominación persistió en el tiempo, dando origen a dos grandes conjuntos numéricos: los números reales y los números complejos, un conjunto más amplio que incluye a los números reales, a los imaginarios y a los que son en parte reales y en parte imaginarios.
La evolución de los números reales siguió su curso hasta que en 1872, el matemático Richard Dedekind (1831-1936) definió con toda formalidad al conjunto de los números reales a través de las llamadas cortaduras de Dedekind. La síntesis de su trabajo fue publicada en un artículo que vio la luz ese mismo año.
Índice del artículo
- 1 Ejemplos de números reales
- 2 Propiedades de los números reales
- 3 Operaciones con números reales
- 4 Aplicaciones
- 5 Ejercicio resuelto
- 6 Referencias
El siguiente cuadro muestra ejemplos de números reales. Dicho conjunto tiene como subconjuntos a los números naturales, los enteros, los racionales y los irracionales. Cualquier número de estos conjuntos es, en sí mismo, un número real.
Por lo tanto el 0, los negativos, los positivos, fracciones y decimales son números reales.

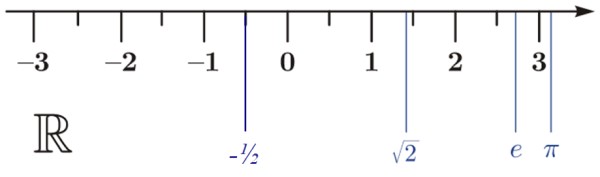
Los números reales se pueden representar sobre la recta real R, como se muestra en la figura. No es necesario que el 0 siempre esté presente, sin embargo es conveniente saber que a su izquierda están los reales negativos y a la derecha los positivos. Por eso es un excelente punto de referencia.
Sobre la recta real se toma una escala, en la cual se encuentran los enteros: …3, -2, -1, 1, 2, 3…. La flecha indica que la recta se extiende hasta infinito. Pero eso no es todo, en cualquier intervalo considerado, también encontraremos siempre infinitos números reales.
Los números reales se representan en orden. Para comenzar está el orden de los números enteros, en los cuales los positivos siempre son mayores que 0, mientras que los negativos son menores.
Este orden se mantiene dentro de los números reales. Las siguientes desigualdades se muestran a modo de ejemplo:
a) -1/2 √2
b) e π
c) π > -1/2
-Los números reales incluyen a los números naturales, los enteros, los racionales y los irracionales.
-Se cumple la propiedad conmutativa de la suma: el orden de los sumandos no altera la suma. Si a y b son dos números reales, siempre se cumple que:
a + b = b + a
-El 0 es el elemento neutro de la suma: a + 0 = a
-Para la suma se cumple la propiedad asociativa. Si a, b y c son números reales: (a + b) + c = a + (b+c).
-El opuesto de un número real a es -a.
-La resta se define como la suma del opuesto: a – b = a + (-b).
-Se cumple la propiedad conmutativa del producto: el orden de los factores no altera el producto: a.b = b.a
-En el producto también se aplica la propiedad asociativa: (a.b).c = a.(b.c)
-El 1 es el elemento neutro de la multiplicación: a.1 = a
-Es válida la propiedad distributiva de la multiplicación respecto de la adición: a. (b+c) = a.b + a.c
-La división por 0 no está definida.
-Cualquier número real a, excepto el 0, tiene inverso multiplicativo a-1 tal que a.a-1 = 1.
-Si a es un número real: a0 = 1 y a1 = a.
-El valor absoluto o módulo de un número real es la distancia entre dicho número y el 0.
Con los números reales se pueden hacer las operaciones que se hacen con los demás conjuntos numéricos, incluyendo suma, resta, multiplicación, división, potenciación, radicación, logaritmos y más.
Como siempre, la división por 0 no está definida, tampoco existen los logaritmos de números negativos ni de 0, aunque se cumple que el log 1 = 0 y que los logaritmos de números entre 0 y 1 son negativos.
Las aplicaciones de los números reales a todo tipo de situaciones son sumamente variadas. Los números reales aparecen como respuesta a muchos problemas en ciencias exactas, computación, ingeniería, economía y ciencias sociales.
Todo tipo de magnitudes y cantidades como distancias, tiempos, fuerzas, intensidad del sonido, dinero y muchas más, tienen su expresión en los números reales.
La transmisión de señales telefónicas, la imagen y el sonido de un video, la temperatura de un aire acondicionado, de un calefactor o de un refrigerador pueden controlarse digitalmente, lo cual significa transformar magnitudes físicas en secuencias numéricas.
Lo mismo sucede cuando se hace una transacción bancaria por Internet o se consulta la mensajería instantánea. Los números reales están por doquier.
Vamos a ver con ejercicios cómo funcionan estos números en situaciones comunes con las que nos encontramos a diario.
La oficina de correos solamente acepta paquetes para los cuales el largo, más la medida del contorno, no exceda 108 pulgadas. Por lo tanto, para que el paquete mostrado sea aceptado, se debe cumplir que:
L + 2(x+y) ≤ 108
a) ¿Logrará pasar un paquete que mide 6 pulgadas de ancho, 8 pulgadas de alto y 5 pies de largo?
b) ¿Qué hay de uno que mida 2 x 2 x 4 pies3?
c) ¿Cuál es el mayor alto aceptable para un paquete cuya base es cuadrada y mide 9 x 9 pulgadas2?
Respuesta a
L = 5 pies = 60 pulgadas
x = 6 pulgadas
y = 8 pulgadas
La operación a resolver es:
L + 2(x+y) = 60 + 2 (6 + 8) pulgadas = 60 + 2 x 14 pulgadas = 60 + 28 pulgadas = 88 pulgadas
El paquete es aceptado.
Respuesta b
Las dimensiones de este paquete son menores que las del paquete a), así que ambos logran pasar.
Respuesta c
En este paquete:
x= L = 9 pulgadas
Se debe cumplir que:
9+ 2(9+y) ≤ 108
27 + 2y ≤ 108
2y ≤ 81
y ≤ 40.5 pulgadas
- Carena, M. 2019. Manual de Matemática Preuniversitaria. Universidad Nacional del Litoral.
- Diego, A. Números reales y sus propiedades. Recuperado de: matematica.uns.edu.ar.
- Figuera, J. 2000. Matemática 9no. Grado. ediciones CO-BO.
- Jiménez, R. 2008. Álgebra. Prentice Hall.
- Stewart, J. 2006. Precálculo: Matemáticas para el Cálculo. 5ta. Edición. Cengage Learning.
