Ecuaciones de primer grado: fórmula, cómo resolverlas, ejemplo, ejercicios
Las ecuaciones de primer grado o lineales con una incógnita son aquellas que pueden expresarse como la suma de dos términos, en la forma siguiente:
ax + b = 0
Donde a y b, con a ≠ 0, son números reales R o también complejos C. Para resolverla se transponen términos, lo que significa cambiar términos de un lado a otro de la igualdad.

Para despejar la incógnita se transpone el término +b, que debe ir al lado derecho de la igualdad con signo cambiado.
ax = -b
Después se despeja el valor de x, de esta forma:
x = – b/a
A modo de ejemplo vamos a resolver la siguiente ecuación:
6x – 5 = 4
Transponemos el término -5 hacia el lado derecho con signo cambiado:
6x = 4 + 5
Esto equivale a sumar 5 a ambos lados de la ecuación original:
6x – 5 + 5 = 4 + 5 → 6x = 9
Y ahora despejamos la incógnita “x”:
x = 9/6 = 3/2
Que equivale a dividir a ambos lados de la igualdad por 6. Así que podemos valernos de lo siguiente para obtener la solución:
-Se puede sumar o restar la misma cantidad a ambos lados de la igualdad en una ecuación, sin alterarla.
-También se puede multiplicar (o dividir) por la misma cantidad a todos los términos tanto a la izquierda como a la derecha de la ecuación.
-Y si ambos miembros de una ecuación se elevan a la misma potencia, la igualdad tampoco se altera.
Índice del artículo
- 1 Cómo resolver ecuaciones de primer grado
- 2 Ejemplos de ecuaciones lineales sencillas
- 3 Ejercicios resueltos sencillos
- 4 Referencias
La solución de una ecuación de primer grado también se conoce como raíz de la misma. Es el valor de x que convierte la expresión original en una igualdad. Por ejemplo en:
5x = 8x – 15
Si sustituimos x = 5 en esta ecuación, se obtiene:
5⋅5 = 8⋅5 – 15
25 = 40 – 15
25 = 25
Como las ecuaciones lineales de primer grado vienen en muchas formas, que a veces no son evidentes, hay una serie de reglas generales que comprenden varias manipulaciones algebraicas, con la finalidad de encontrar el valor de la incógnita:
-En primer lugar, si hay operaciones indicadas, estas deben llevarse a cabo.
-Los símbolos de agrupación como paréntesis, corchetes y llaves, en caso de existir, deben suprimirse manteniendo los signos adecuados.
-Los términos se transponen para colocar todos los que contienen la incógnita a un solo lado de la igualdad, y los que no la contienen al otro.
-Seguidamente se reducen todos los términos semejantes, para llegar a la forma ax = -b.
–Y el último paso es despejar la incógnita.
La ecuación de primer grado planteada al comienzo se puede derivar de la ecuación de la recta y = mx+c, haciendo y = 0. El valor de x que resulta corresponde a la intersección de la recta con el eje horizontal.
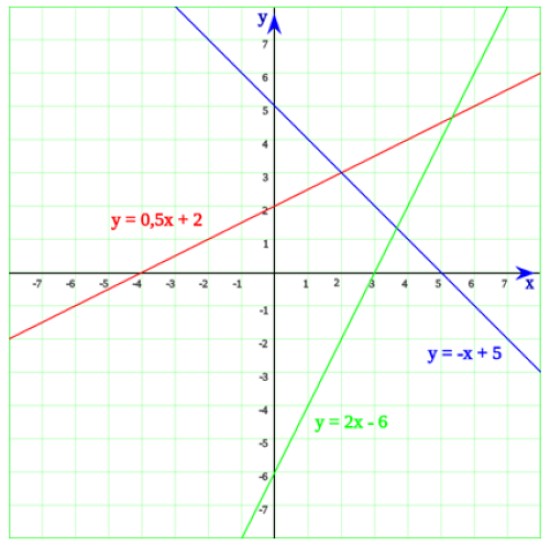
En la siguiente figura se tienen tres rectas. Comenzando por la recta de color verde, cuya ecuación es:
y = 2x – 6
Haciendo y = 0 en la ecuación de la recta se obtiene la ecuación de primer grado:
2x – 6 = 0
Cuya solución es x = 6/2 = 3. Ahora cuando detallamos la gráfica, es fácil darse cuenta de que en efecto, la recta corta al eje horizontal en x = 3.
La recta de color azul intersecta al eje x en x = 5, que es la solución a la ecuación –x + 5 = 0. Por último, la recta cuya ecuación es y = 0.5x + 2 corta al eje x en x = -4, lo cual se advierte fácilmente de la ecuación de primer grado:
0.5 x + 2 = 0
x = 2/0.5 = 4
Son aquellas en cuyos términos no hay denominadores, por ejemplo:
21 – 6x = 27 – 8x
Su solución es:
-6x + 8x = 27 – 21
2x = 6
x = 3
Estas ecuaciones contienen al menos un denominador diferente de 1. Para resolverlas es recomendable multiplicar todos los términos por el mínimo común múltiplo (mcm) de los denominadores, a fin de suprimirlos.
La siguiente ecuación es de tipo fraccionario:
Como estos números son pequeños, no es difícil ver que m.c.m (6, 8,12) = 24. Este resultado se obtiene fácilmente al expresar los números como producto de números primos o sus potencias, veamos:
6 = 3.2
8 = 23
12 = 22⋅3
El mínimo común múltiplo se determina al multiplicar los factores comunes y no comunes de 6, 8 y 12 con su mayor exponente, entonces:
mcm (6,8,12) = 23 ⋅3 = 8 × 3 = 24
Ya que se cuenta con el mínimo común múltiplo hay que multiplicarlo por cada uno de los términos de la ecuación:
4(x+5) -3(2x+3) = 2(1-5x)
Hacemos uso de la propiedad distributiva:
4x + 20 – 6x -9 = 2 – 10x
Se agrupan todos los términos que contienen la incógnita “x” al lado izquierdo de la igualdad, dejando los términos independientes o numéricos del lado derecho:
4x – 6x + 10 x = 2 +9 – 20
8x = -9
x = – 9/8
Son ecuaciones lineales con una incógnita, que sin embargo vienen acompañadas de coeficientes literales (letras). Estas letras se tratan al igual que se haría con los números. Un ejemplo de ecuación de primer grado literal es:
-3ax + 2a = 5x – b
Esta ecuación se soluciona del mismo modo que si los términos independientes y los coeficientes fueran numéricos:
-3ax – 5x = – b – 2a
Factorizando la incógnita “x”:
x (-3a – 5) = – b – 2a
x = (- b – 2a) / (-3a – 5) → x = (2a + b) / (3a + 5)
Los sistemas de ecuaciones constan de un conjunto de ecuaciones con dos o más incógnitas. La solución del sistema consiste en valores que satisfacen las ecuaciones simultáneamente y para determinarla de manera inequívoca, debe haber una ecuación por cada incógnita.
La forma general de un sistema de m ecuaciones lineales con n incógnitas es:
a11x1 + a12x2 + … a1nxn = b1
a21x1 + a22x2 + … a2nxn = b2
…
am1x1 + am2x2 + … amnxn = bm
Si el sistema tiene solución se dice que es compatible determinado, cuando existe un conjunto infinito de valores que lo satisfacen es compatible indeterminado, y finalmente, si no tiene solución, entonces es incompatible.
En la resolución de los sistemas de ecuaciones lineales se emplean varios métodos: reducción, sustitución, igualación, métodos gráficos, eliminación de Gauss-Jordan y el uso de determinantes están entre los más utilizados. Pero existen otros algoritmos para llegar a la solución, más convenientes para sistemas con muchas ecuaciones e incógnitas.
Un ejemplo de sistema de ecuaciones lineales con dos incógnitas es:
8x – 5 = 7y – 9
6x = 3y + 6
La solución de este sistema se presenta más adelante en la sección de ejercicios resueltos.
El valor absoluto de un número real es la distancia que hay entre su ubicación sobre la recta numérica y el 0 de la misma. Al tratarse de una distancia su valor siempre es positivo.
El valor absoluto de un número se denota mediante las barras de módulo: │x│. El valor absoluto de un número positivo o negativo siempre es positivo, por ejemplo:
│+8│ = 8
│-3│ = 3
En una ecuación con valor absoluto, la incógnita se encuentra entre barras de módulo. Consideremos la siguiente ecuación sencilla:
│x│ = 10
Existen dos posibilidades, la primera es que x sea un número positivo, en cuyo caso tenemos:
x = 10
Y la otra posibilidad es que x sea un número negativo, en este caso:
x = -10
Estas son las soluciones de esta ecuación. Ahora veamos un ejemplo diferente:
│x+6│ = 11
La cantidad dentro de las barras puede ser positiva, entonces:
x+6 = 11
x = 11 -6 = 5
O puede ser negativa. En tal caso:
-(x+6) = 11
-x – 6 = 11 ⇒ -x = 11+6 = 17
Y el valor de la incógnita es:
x = -17
Esta ecuación de valor absoluto tiene por lo tanto dos soluciones: x1 = 5 y x2 = -17. Podemos comprobar que ambas soluciones conducen a una igualdad en la ecuación original:
│5+6│ = 11
│11│ = 11
Y
│-17+6│ = 11
│-11│ = 11
Resolver el siguiente sistema de ecuaciones lineales con dos incógnitas:
8x – 5 = 7y -9
6x = 3y + 6
Solución
Tal como está planteado este sistema es idóneo para emplear el método de sustitución, ya que en la segundo ecuación la incógnita x está casi lista para el despeje:
x = (3y + 6)/6
Y se puede sustituir de inmediato en la primera ecuación, que entonces se convierte en una ecuación de primer grado con incógnita “y”:
8[(3y + 6)/6] – 5 = 7y – 9
El denominador se puede suprimir si se multiplica cada término por 6:
6 . 8⋅[(3y + 6)/6] – 6.5 = 6 .7y– 6 . 9
8⋅(3y + 6) – 30 = 42y – 54
Aplicando la propiedad distributiva en el primer término a la derecha de la igualdad:
24y + 48 -30 = 42y – 54 ⇒ 24y + 18 = 42y – 54
La ecuación se puede simplificar, ya que todos los coeficientes son múltiplos de 6:
4y + 3 = 7y – 9
-3y = -12
y = 4
Con este resultado vamos al despeje de x:
x = (3y +6)/6 → x = (12+6)/6 = 3
Resolver la siguiente ecuación:
Solución
En esta ecuación aparecen productos, y siguiendo las instrucciones dadas al comienzo, hay que desarrollarlos en primer lugar:
3x – 10x +14 = 5x + 36x + 12
Luego se llevan todos los términos que contienen las incógnitas al lado izquierdo de la igualdad, y al lado derecho estarán los términos independientes:
3x – 10x – 5x – 36x = 12 – 14
-48x = -2
x = 1/24
Al sumar los tres ángulos interiores de un triángulo se obtiene 180º. El mayor excede al menor en 35º, y este a su vez excede en 20º la diferencia existente entre el mayor y el mediano. ¿Cuáles son los ángulos?
Solución
Llamaremos “x” al ángulo mayor, “y” al del medio y “z” al menor. Cuando el enunciado afirma que la suma de ellos es 180º se puede escribir:
x + y + z = 180
Después sabemos que el mayor excede al menor en 35º, esto lo podemos escribir así:
x = z + 35
Por último el menor excede en 20 º a la diferencia que hay entre el mayor y el mediano:
z = x – y + 20
Tenemos un sistema de 3 ecuaciones y 3 incógnitas:
x + y + z = 180
x = z + 35
z = x – y + 20
Al despejar z de la primera ecuación se tiene:
z = 180 – x – y
Igualando con la tercera:
180 – x – y = x – y + 20
Pasando las incógnitas al lado izquierdo como siempre:
-x – y – x + y = 20 – 180
La “y” se cancela y queda:
-2x = – 160
x = 80º
De la segunda ecuación se halla el valor de z:
z = x – 35 = 80 – 35 = 45º
Y el valor de y se encuentra de la primera o la tercera:
y = 180 – x – z = 180 – 80 – 45 = 55º
- Baldor. 1977. Álgebra Elemental. Ediciones Cultural Venezolana.
- Monterey Institute. Ecuaciones, desigualdades y valor absoluto. Recuperado de: montereyinstitute.org.
- Profesor en línea. Clasificación de ecuaciones lineales o de primer grado. Recuperado de: profesorenlinea.cl.
- Hoffman, J. Selección de temas de Matemática. Volumen 2.
- Jiménez, R. 2008. Álgebra. Prentice Hall.
- Zill, D. 1984. Álgebra y Trigonometría. McGraw Hill.
