Perímetro del círculo: cómo sacarlo y fórmulas, ejercicios resueltos
El perímetro del círculo es el conjunto de puntos que forman el contorno de un círculo y también se conoce como longitudde la circunferencia. Depende del radio, pues una circunferencia más grande, evidentemente tendrá un contorno mayor.
Sea P el perímetro de un círculo y R el radio del mismo, entonces podemos calcular P con la siguiente ecuación:
P = 2π.R

Donde π es un número real (se lee “pi”) que vale aproximadamente 3.1416… Los puntos suspensivos se deben a que π tiene infinitos decimales. Por ello a la hora de hacer los cálculos, es necesario redondear su valor.
Sin embargo para la mayoría de las aplicaciones basta con tomar la cantidad indicada aquí, o bien emplear todos los decimales que arroje la calculadora con la que se trabaje.
Si en vez de tener el radio, se prefiere utilizar el diámetro D, que sabemos es el doble del radio, el perímetro se expresa así:
P = π.2R= π.D
Como el perímetro es una longitud, debe venir siempre expresado en unidades tales como metros, centímetros, pies, pulgadas y más, según el sistema que se prefiera.
Índice del artículo
- 1 Circunferencias y círculos
- 2 Ejercicios de demostración del cálculo del perímetro del círculo
- 3 Aplicaciones
- 4 Referencias
Con frecuencia son términos que se utilizan indistintamente, es decir, como sinónimos. Pero ocurre que sí hay diferencias entre ellos.
La palabra “perímetro” proviene del griego “peri” que significa contorno y “metro” o medir. La circunferencia es el contorno o perímetro del círculo. Formalmente se define así:
Una circunferencia es el conjunto de puntos con igual distancia a un punto llamado centro, siendo esta distancia el radio de la circunferencia.
Por su parte, el círculo se define así:
Un círculo es el conjunto de puntos cuya distancia a un punto llamado centro es menor o igual a una distancia fija llamada radio.
El lector puede advertir la diferencia sutil entre ambos conceptos. La circunferencia solamente se refiere al conjunto de puntos del borde, mientras que el círculo es el conjunto de puntos desde el borde hasta el interior, de la cual la circunferencia es la frontera.
Mediante los siguientes ejercicios, se pondrán en práctica los conceptos antes descritos, así como algunos otros que se irán explicando a medida que vayan apareciendo. Comenzaremos desde lo más sencillo y se irá aumentando el grado de dificultad progresivamente.
Hallar el perímetro y el área del círculo de radio 5 cm.
Solución
Se aplica directamente la ecuación dada al comienzo:
P = 2π.R= 2π.5 cm =10 π cm = 31.416 cm
Para calcular el área A se emplea la siguiente fórmula:
A = π.R2 = π. (5cm)2= 25π cm2= 78.534 cm2
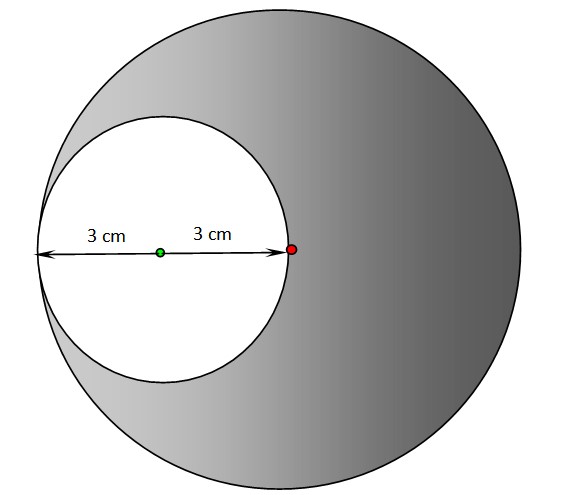
a) Encuentre el perímetro y el área de la región en blanco de la siguiente figura. El centro del círculo sombreado está en el punto rojo, mientras que el centro de la circunferencia blanca es el punto verde.
b) Repita el apartado anterior para la región sombreada.
Solución
a) El radio de la circunferencia blanca es de 3 cm, por lo tanto aplicamos las mismas ecuaciones que en el ejercicio 1:
P = 2π.R= 2π.3 cm =6 π cm = 18.85 cm
A = π.R2 = π. (3cm)2= 9π cm2= 28.27 cm2
b) Para el círculo sombreado, el radio es de 6 cm, su perímetro es el doble del que se calculó en el apartado a):
P = 2π.R= 2π.6 cm =12 π cm = 37.70 cm
Y finalmente el área de la región sombreada se calcula de la siguiente forma:
– Primero se encuentra el área del círculo sombreado como si estuviera completo, a la cual llamaremos A´, así:
A´ = π.R2= π.(6 cm)2 =36π cm2= 113.10 cm2
– Después, al área A´ se le resta el área del círculo blanco, calculada previamente en el apartado a), de esta forma se obtiene el área solicitada, la cual se denotará simplemente como A:
A = A´ – 28.27 cm2 = 113.10-28.27 cm2 = 84.83 cm2
Hallar el área y el perímetro de la región sombreada en la siguiente figura:

Solución
Cálculo del área de la región sombreada
Calculamos primero el área del sector circular o cuña, comprendido entre los segmentos rectos OA y OB y el segmento circular AB, como se muestra en la siguiente figura:
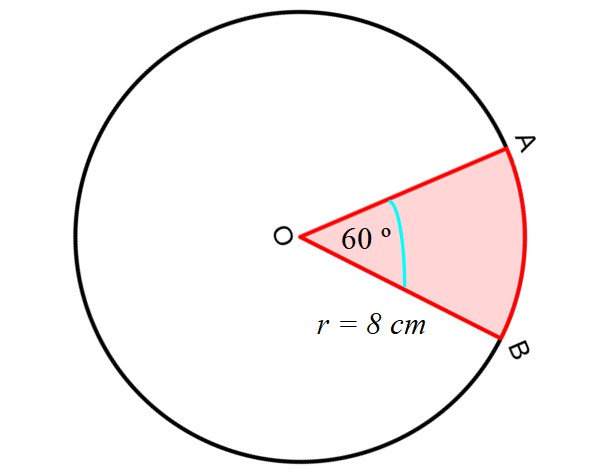
Para ello se emplea la siguiente ecuación, que nos da el área de un sector circular, conociendo el radio R y el ángulo central comprendido entre los segmentos OA y OB, es decir, dos de los radios de la circunferencia:
A sector circular = π.R2. (αº/360º)
Donde αº es el ángulo central –es central porque su vértice es el centro de la circunferencia- comprendido entre dos radios.
Paso 1: cálculo del área del sector circular
De esta forma, el área del sector mostrado en la figura es:
A sector circular = π.R2. (αº/360º) = π. (8 cm)2. (60º/360º) = (64/6) π cm2= 33.51 cm2
Paso 2: cálculo del área del triángulo
Seguidamente calcularemos el área del triángulo blanco de la figura 3. Dicho triángulo es equilátero y su área es:
A triángulo = (1/2) base x altura
La altura es la línea roja punteada que se ve en la figura 4. Para encontrarla se puede usar el teorema de Pitágoras, por ejemplo. Pero no es la única forma.
El lector observador habrá notado que el triángulo equilátero queda dividido en dos triángulos rectángulos idénticos, cuya base es 4 cm:

En un triángulo rectángulo se cumple el teorema de Pitágoras, por lo tanto:
A triángulo = (1/2) base x altura = (1/2) 8 cm x 6.93 cm = 27.71 cm2.
Paso 3: cálculo del área sombreada
Basta con restar el área mayor (la del sector circular) del área menor (la del triángulo equilátero): A región sombreada = 33.51 cm2 – 27.71 cm2 = 5.80 cm2.
Cálculo del perímetro de la región sombreada
El perímetro buscado es la suma del lado rectilíneo de 8 cm y el arco de circunferencia AB. Ahora bien, la circunferencia completa subtiende 360 º, por lo tanto un arco que subtiende 60 º es una sexta parte de la longitud completa, la cual sabemos que es 2.π.R:
AB = 2.π.R / 6 = 2.π.8 cm / 6 = 8.38 cm
Sustituyendo, el perímetro de la región sombreada es:
P = 8 cm + 8.38 cm = 16.38 cm.
El perímetro, al igual que el área, es un concepto muy importante en la geometría y con muchas aplicaciones en la vida diaria.
Artistas, diseñadores, arquitectos, ingenieros y muchas otras personas hacen uso del perímetro mientras desarrollan su trabajo, sobre todo el de un círculo, pues la forma redonda está por todos lados: desde la publicidad, pasando por los alimentos hasta las maquinarias.

Para conocer directamente la longitud de una circunferencia basta con envolverla con un hilo o cordel, luego extender este hilo y medirlo con una cinta métrica. La otra alternativa es medir el radio o el diámetro del círculo y emplear alguna de las fórmulas descritas arriba.
En el quehacer diario se utiliza el concepto de perímetro cuando:
-Se escoge el molde adecuado para un cierto tamaño de pizza o pastel.
-Va a diseñarse una vía urbana, al calcular el tamaño de una redoma donde los coches pueden girar para cambiar de sentido.
-Conocemos que la Tierra gira alrededor del Sol en una órbita aproximadamente circular –en realidad las órbitas planetarias son elípticas, según las leyes de Kepler-, pero la circunferencia es una muy buena aproximación para la mayoría de los planetas.
-Se elige el tamaño apropiado de una sortija o anillo que se va a comprar en una tienda online.
-Escogemos una llave del tamaño adecuado para aflojar una tuerca.
Y muchísimas más.
- Free Mathematics Tutorials. Area and Perimeter of a Circle – Geometry Calculator. Recuperado de: analyzemath.com.
- Math Open Reference. Circumference, Perimeter of a circle. Recuperado de: mathopenref.com.
- Monterey Institute. Perímetro y Área. Recuperado de: montereyinstitute.org.
- Sciencing. How to find the Perimeter of a Circle. Recuperado de: sciencing.com.
- Wikipedia. Circumference. Recuperado de: en.wikipedia.org.
