Tiro parabólico oblicuo: características, fórmulas, ecuaciones, ejemplos
El tiro parabólico oblicuo es un caso particular del movimiento de caída libre en el que la velocidad inicial del proyectil forma cierto ángulo con la horizontal, dando como consecuencia una trayectoria parabólica.
La caída libre es un caso de movimiento con aceleración constante, en el que la aceleración es la de la gravedad, la cual apunta siempre verticalmente hacia abajo y tiene una magnitud de 9,8 m/s^2. No depende de la masa del proyectil, tal como lo demostró Galileo Galilei en 1604.
Si la velocidad inicial del proyectil es vertical, la caída libre tiene trayectoria recta y vertical, pero si la velocidad inicial es oblicua entonces la trayectoria de caída libre es una curva parabólica, hecho también demostrado por Galileo.
Son ejemplos de movimiento parabólico la trayectoria que sigue una pelota de béisbol, la bala disparada por un cañón y el chorro del agua que sale de una manguera.
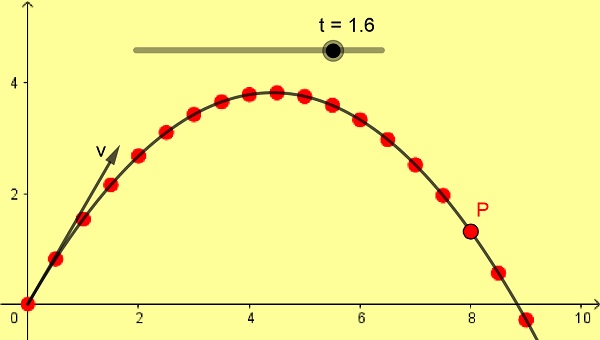
La figura 1 muestra un tiro parabólico oblicuo de 10 m/s con un ángulo de 60º. La escala está en metros y las sucesivas posiciones de P están tomadas con diferencia de 0,1 s partiendo del instante inicial 0 segundos.
Índice del artículo
El movimiento de una partícula se describe completamente si se conoce su posición, su velocidad y su aceleración como función del tiempo.
El movimiento parabólico resultante de un disparo oblicuo es la superposición de un movimiento horizontal a velocidad constante, más un movimiento vertical con aceleración constante igual a la aceleración de gravedad.
Las fórmulas que se aplican al tiro parabólico oblicuo son la que corresponden a un movimiento con aceleración constante a = g, note que se ha usado negrita para indicar que la aceleración es una cantidad vectorial.
En un movimiento con aceleración constante la posición depende matemáticamente del tiempo en forma cuadrática.
Si denotamos r(t) la posición al tiempo t, ro la posición al instante inicial, vo la velocidad inicial, g la aceleración y t=0 como el instante inicial la fórmula que da la posición para cada instante de tiempo t es:
r(t) = ro + vo t + ½ g t2
Las negritas en la expresión anterior indican que se trata de una ecuación vectorial.
La velocidad como función del tiempo se obtiene de tomar la derivada con respecto a t de la posición y el resultado es:
v(t) = vo + g t
Y para obtener la aceleración como función del tiempo se toma la derivada de la velocidad con respecto a t dando como resultado:
a(t) = g
Cuando no se dispone del tiempo, existe una relación entre la velocidad y la posición, que viene dada por:
v2 = vo2 – 2 g (y – yo )
A continuación encontraremos las ecuaciones que se aplican a un tiro parabólico oblicuo en forma cartesiana.
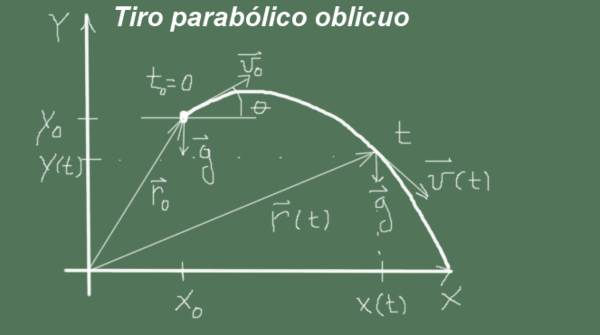
El movimiento comienza en el instante t=0 con posición inicial (xo, yo) y velocidad de magnitud vo y ángulo θ, es decir que el vector velocidad inicial es ( vo cosθ, vo senθ ). El movimiento transcurre con aceleración
g = (0, -g).
Si se aplica la fórmula vectorial que da la posición como función del tiempo y se agrupan e igualan componentes, se obtendrá entonces las ecuaciones que dan las coordenadas de la posición a cualquier instante de tiempo t.
x(t) = xo + vox t
y(t) = yo + voy t -½ g t2
De forma similar, se tienen las ecuaciones para las componentes de la velocidad como función del tiempo.
vx(t) = vox
vy(t) = voy – g t
Donde: vox = vo cosθ ; voy = vo senθ
y = A x^2 + B x + C
A = -g/(2 vox^2)
B = ( voy/vox + g xo/vox^2)
C = (yo – voy xo / vox)
Responder las siguientes preguntas:
a) ¿Por qué en los problemas de tiro parabólico suele despreciarse el efecto de la fricción con el aire?
b) ¿Tiene alguna importancia la forma del objeto en el tiro parabólico?
Respuestas
a) Para que el movimiento de un proyectil sea parabólico es importante que la fuerza de fricción del aire sea mucho menor que el peso del objeto que se lanza.
Si se lanza una pelota de corcho o de algún material liviano, la fuerza de fricción es comparable al peso y su trayectoria no puede aproximarse a una parábola.
Por el contrario, si se trata de un objeto pesado como una piedra, la fuerza de fricción es despreciable comparada con el peso de la piedra y su trayectoria sí se aproxima a una parábola.
b) La forma del objeto que se lanza también es relevante. Si se lanza una hoja de papel en forma de avioncito su movimiento no será de caída libre ni parabólica, ya que la forma favorece la resistencia del aire.
En cambio, si la misma hoja de papel se compacta en forma de pelotita, el movimiento resultante es muy semejante a una parábola.
Un proyectil se lanza desde el suelo horizontal con rapidez de 10 m/s y ángulo de 60º. Estos son los mismos datos con los que se elaboró la figura 1. Con estos datos halle:
a) Instante en el que alcanza la máxima altura.
b) La altura máxima.
c) La velocidad en la altura máxima.
d) La posición y la velocidad a los 1,6 s.
e) El instante en que toca suelo nuevamente.
f) El alcance horizontal.
Solución a)
La velocidad vertical en función del tiempo es
vy(t) = voy – g t = vo senθ – g t = 10 sen60º – 9.8 t =8.66 – 9.8 t
En el momento que se alcanza la altura máxima la velocidad vertical es cero por un instante.
8.66 – 9.8 t = 0 ⇒ t = 0.88 s.
Solución b)
La altura máxima está dada por la coordenada y para el instante en el que se alcanza esa altura:
y(0.88s) = yo + voy t -½ g t^2 = 0 + 8.66*0.88-½ 9.8 0.88^2 =
3.83 m
Por lo tanto la altura máxima es 3.83 m.
Solución c)
La velocidad en la altura máxima es horizontal:
vx(t) = vox = vo cosθ = 10 cos60º = 5 m/s
Solución d)
La posición a los 1.6 s es:
x(1.6) = 5*1,6 = 8,0 m
y(1.6) = 8.66*1.6-½ 9.8 1.62 = 1.31 m
Solución e)
Cuando toca suelo la coordenada y se anula, luego:
y(t) = 8.66*t-½ 9.8 t2 = 0 ⇒ t=1,77 s
Solución f)
El alcance horizontal es la coordenada x justo en el instante que toca suelo:
x(1.77) = 5*1,77 = 8,85 m
Halle la ecuación de la trayectoria con los datos del ejemplo 2.
Solución
La ecuación paramétrica de la trayectoria es:
x(t) = 5*t
y(t) = 8.66*t-½ 9.8 t^2
Y la ecuación cartesiana se obtiene despejando t de la primera y sustituyendo en la segunda
y = 8.66*(x/5)-½ 9.8 (x/5)^2
Simplificando:
y = 1,73 x – 0,20 x^2
- P. P. Teodorescu (2007). «Kinematics». Mechanical Systems, Classical Models: Particle Mechanics. Springer.
- Resnick, Halliday & Krane (2002). Física Volumen 1. Cecsa, México.
- Thomas Wallace Wright (1896). Elements of Mechanics Including Kinematics, Kinetics and Statics. E and FN Spon.
- Wikipedia. Movimiento parabólico. Recuperado de es.wikipedia.org.
- Wikipedia. Projectile motion.Recuperado de en.wikipedia.org.
