Suavizamiento exponencial: método y ejemplo
El suavizamiento exponencial es una forma de pronosticar la demanda de un artículo para un período dado. Este método estima que la demanda será igual al promedio de los consumos históricos en un período dado, dándole un mayor peso o ponderación a los valores que se encuentren más cercanos en el tiempo. Adicionalmente, para los siguientes pronósticos toma en cuenta el error existente del pronóstico actual.
El pronóstico de la demanda es el método para proyectar la demanda de un producto o servicio por parte de los clientes. Este proceso es continuo, donde los gerentes usan datos históricos para calcular lo que esperan que sea la demanda de ventas de un bien o servicio.
Se usa la información del pasado de la compañía agregándola a los datos económicos del mercado para ver si las ventas aumentarán o disminuirán.
Los resultados del pronóstico de la demanda se utilizan para establecer objetivos para el departamento de ventas, tratando de mantenerse en línea con los objetivos de la empresa.
Índice del artículo
Suavizar es un proceso estadístico muy común. Con frecuencia se encuentran datos suavizados en diversas formas de la vida cotidiana. Cada vez que se usa un promedio para describir algo, se está utilizando un número suavizado.
Supongamos que este año se experimentó el invierno más cálido registrado. Para cuantificarlo, se comienza con el conjunto de datos diarios de temperaturas para el período de invierno de cada año histórico registrado.
Esto genera una cantidad de números con grandes “brincos”. Se necesita un número que elimine todos estos brincos de los datos para poder comparar más fácilmente un invierno con otro.
Eliminar el brinco en los datos se denomina suavizamiento. En este caso se puede usar un simple promedio para lograr el suavizado.
Para el pronóstico de la demanda igualmente se utiliza el suavizamiento para eliminar las variaciones de la demanda histórica. Esto permite identificar mejor los patrones de la demanda, que se pueden utilizar para estimar la demanda futura.
Las variaciones en la demanda es el mismo concepto que el “brinco” de los datos de temperatura. La forma más común en que se eliminan las variaciones del historial de demanda es utilizando un promedio, o específicamente, un promedio móvil.
El promedio móvil utiliza un número predefinido de períodos para calcular el promedio, y esos períodos se van moviendo a medida que pasa el tiempo.
Por ejemplo, si se utiliza un promedio móvil de cuatro meses y hoy es 1 de mayo, se usará el promedio de la demanda ocurrida en enero, febrero, marzo y abril. El 1 de junio se usará la demanda de febrero, marzo, abril y mayo.
Cuando se usa un promedio simple se aplica la misma importancia a cada valor en el conjunto de datos. Por tanto, en un promedio móvil de cuatro meses, cada mes representa el 25% del promedio móvil.
Al utilizar el historial de demanda para proyectar la demanda futura, es lógico llegar a la conclusión que el período más reciente tenga un mayor impacto en el pronóstico.
Se puede adaptar el cálculo del promedio móvil para aplicar diferentes “pesos” a cada período, para así obtener los resultados deseados.
Estos pesos se expresan como porcentajes. El total de todos los pesos para todos los períodos debe sumar 100%.
Por tanto, si se quiere aplicar 35% como el peso para el período más cercano en el promedio ponderado de cuatro meses, se puede restar 35% del 100%, quedando un 65% para dividir entre los tres períodos restantes
Por ejemplo, se puede terminar con una ponderación de 15%, 20%, 30% y 35% respectivamente para los cuatro meses (15+20+30+35=100).
La entrada de control del cálculo del suavizamiento exponencial se conoce como factor de suavizamiento. Representa la ponderación aplicada a la demanda del período más reciente.
Si se usa 35% como ponderación del período más reciente en el cálculo del promedio móvil ponderado, también se podría elegir usar 35% como factor de suavizado en el cálculo de suavizamiento exponencial.
Parte exponencial
La diferencia en el cálculo de suavizamiento exponencial es que, en lugar de tener que averiguar cuánto peso aplicar a cada período anterior, se usa el factor de suavizado para hacer eso automáticamente.
Esta es la parte “exponencial”. Si se utiliza 35% como factor de suavizado, la ponderación de la demanda del período más reciente será del 35%. La ponderación de la demanda del período anterior al más reciente, será el 65% del 35%.
El 65% proviene de restar 35% del 100%. Esto equivale a 22,75% de ponderación para ese período. La demanda del siguiente período más reciente será el 65% del 65% de 35%, lo que equivale a 14,79%.
El período anterior se ponderará como el 65% del 65% del 65% de 35%, equivalente a 9,61%. Esto se hará para todos los períodos anteriores, hasta llegar al primer período.
Fórmula
La fórmula para calcular el suavizamiento exponencial es la siguiente: (D*S) + (P*(1-S)), donde,
D= demanda más reciente del período.
S= factor de suavizado, representado en forma decimal (35% sería 0,35).
P= pronóstico del período más reciente, resultado del cálculo de suavizado del período anterior.
Asumiendo que se tiene un factor de suavizado de 0,35, se tendría entonces: (D*0,35) + (P*0,65).
Como se puede ver, las únicas entradas de datos necesarias son la demanda y el pronóstico del período más reciente.
Una compañía de seguros ha decidido ampliar su mercado a la ciudad más grande del país, brindando seguros para vehículos.
Como acción inicial, la empresa quiere pronosticar cuántos seguros para vehículos serán comprados por los habitantes de esta ciudad.
Para ello, utilizarán como datos iniciales la cantidad de seguros de carros comprados en otra ciudad más pequeña.
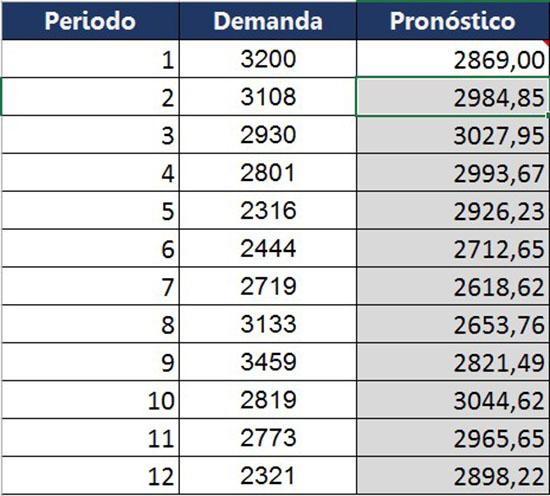
El pronóstico de la demanda para el período 1 es de 2.869 seguros de vehículos contratados, pero la demanda real en ese periodo fue de 3.200.
Según el criterio de la empresa, asigna un factor de suavizado de 0,35. La demanda pronosticada del período siguiente es: P2= (3200*0,35) + 2869*(1-0,35) = 2984,85.
Este mismo cálculo fue realizado para todo el año, consiguiendo la siguiente tabla comparativa entre lo que realmente se obtuvo y lo pronosticado para ese mes.
En comparación a las técnicas de promedios, el suavizamiento exponencial puede predecir la tendencia de mejor manera. Sin embargo, sigue quedándose corto, como se muestra en el gráfico:
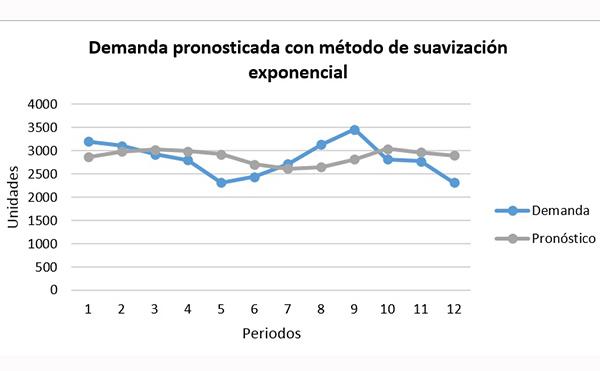
Se puede observar cómo la línea gris del pronóstico puede encontrarse muy por debajo o por arriba de la línea azul de la demanda, sin conseguir seguirle totalmente.
- Wikipedia (2019). Suavizamiento exponencial. Tomado de: es.wikipedia.org.
- Ingenio Empresa (2016). Cómo usar la suavización exponencial simple para pronosticar la demanda. Tomado de: ingenioempresa.com.
- Dave Piasecki (2019). Exponential Smoothing Explained. Tomado de: inventoryops.com.
- Study (2019). Demand Forecasting Techniques: Moving Average & Exponential Smoothing. Tomado de: study.com.
- Cityu (2019). Exponential Smoothing Methods. Tomado de: personal.cb.cityu.edu.hk.
