Toroide o toro dona: qué es, características, volumen, superficie, ejemplos
¿Qué es un toroide?
El toroide es un cuerpo geométrico tridimensional en forma de aro, anillo, argolla, rosquilla o donut, de allí el nombre de “toro dona”, perteneciente a la clase de objetos llamados sólidos de revolución.
Se genera un toroide mediante la rotación de una figura plana cerrada, en torno a una recta perteneciente al mismo plano de la figura, pero que no la intercepta, tal como se muestra seguidamente:
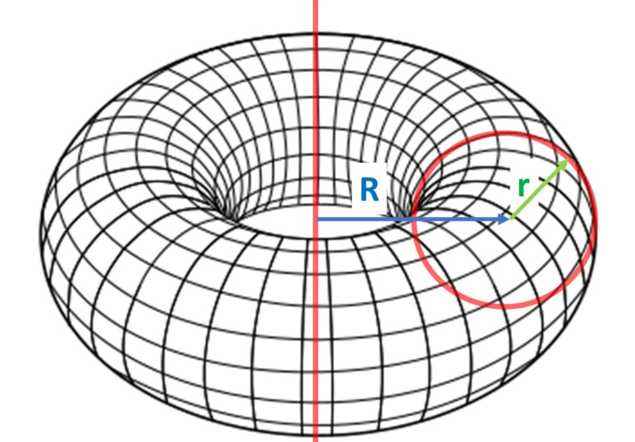
La principal característica del toroide es que, a pesar de ser una superficie cerrada, tiene un hueco. Esto significa que dos puntos de su superficie pueden estar conectados por un segmento que está al exterior del objeto.
Otra característica del toroide es que se trata de una figura tridimensional sin vértices. Esta característica la comparte con otros cuerpos volumétricos como la esfera, pero mientras la esfera es una superficie convexa, el toroide en cambio es simultáneamente cóncavo y convexo.
Entre los toroides, el toro es el más común y se obtiene de la rotación de una circunferencia de radio r, respecto de un eje a distancia R del primero. El radio r (en minúscula) se conoce como el radio menor y el R (en mayúscula) es el radio mayor.
Volumen de un toroide
Un toroide se genera al hacer girar una figura plana cerrada de área A alrededor de un eje de rotación que no la corta. Denotando por R la distancia del eje al centroide de la figura plana, el volumen del toroide de revolución es:
V = 2πR⋅ A
Este resultado se obtiene al aplicar el teorema de Pappus para el volumen de un sólido de revolución, el cual afirma que el volumen de cualquier sólido de revolución se obtiene al multiplicar el área de la figura que se rota por el perímetro de la circunferencia formada por la rotación del centroide (o centro de gravedad) de la figura rotada, en torno al eje de rotación.
Volumen de un toro
El toro es el toroide generado por una circunferencia de radio r. Si la distancia del eje de rotación al centro de la circunferencia girada es R, se tiene entonces que el volumen de dicho toro es:
V = (2πR)⋅ (πR2) = 2π2R3
Superficie de un toroide
Sea una figura plana simplemente conexa de área A y contorno L. Si tal figura se hace rotar en torno a un eje contenido en el mismo plano de la figura, pero que no cruza a la misma, entonces la superficie generada es un toroide de área:
S = 2πR⋅ L
Siendo R la distancia del eje al centro de gravedad o centroide, de la figura generatriz.
Este resultado es consecuencia del teorema de Pappus para la superficie de un sólido de revolución.
Superficie de un toro
El toroide de sección transversal circular de radio r (minúscula) y radio mayor R (mayúscula) es un toroide particular llamado toro.
Como el contorno L de un círculo de radio r es 2πr, entonces el área de la superficie de dicho toro es:
S = (2πR) ⋅ (2πr) = (4π2)(R⋅ r)
Aplicaciones del toroide
Por sus características geométricas, el toroide tiene sinnúmero de aplicaciones prácticas y culturales. Para comenzar, los aros o anillos son piezas de forma toroidal los cuales tienen diversos usos:
Culturales
- Uso ornamental o cosmético cuando se coloca un anillo en un dedo, o cuando se coloca un piercing en la oreja.
- En la nariz de los bueyes se coloca un aro, el cual sirve para amarrarlo y controlarlo.
- Cuando el aro o anillo se coloca en la mano izquierda en el dedo anular, entonces tiene una connotación social, que data desde la época de los antiguos griegos, y denota compromiso, fidelidad y matrimonio con la pareja que porte un aro de igual forma y material.
En mecánica
Fuera del contexto ornamental, cosmético y cultural, el toroide tiene muchas aplicaciones prácticas. En mecánica, el toroide se usa como aro de retención de los cojinetes en la punta de eje de los vehículos.
También los rodamientos de los vehículos automotores están constituidos por uno o dos aros de forma toroidal con diversas formas de sección transversal, sobre los cuales ruedan cilindros o esferas, con el propósito de reducir la fricción en los ejes.
En electricidad
En las aplicaciones eléctricas el toroide también es de suma importancia, ya que los núcleos ferromagnéticos de inductores, electroimanes y transformadores, frecuentemente tienen forma toroidal y sobre los mismos se arrolla un cable en forma de bobina.
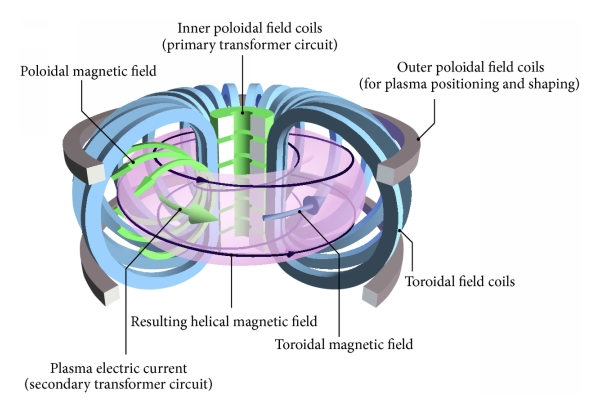
El tokamak
Hay un tipo de reactor de fusión controlada en forma de toroide o donut llamado por su nombre ruso: tokamak. En este tipo de reactor de fusión nuclear, el recipiente y las bobinas que producen el campo magnético de confinamiento del plasma tienen forma o disposición toroidal.
Ejemplos
Superficie de un toroide de sección cuadrada (por fórmula)
En este ejemplo se considera un toroide de sección cuadrada como el mostrado en la siguiente figura:
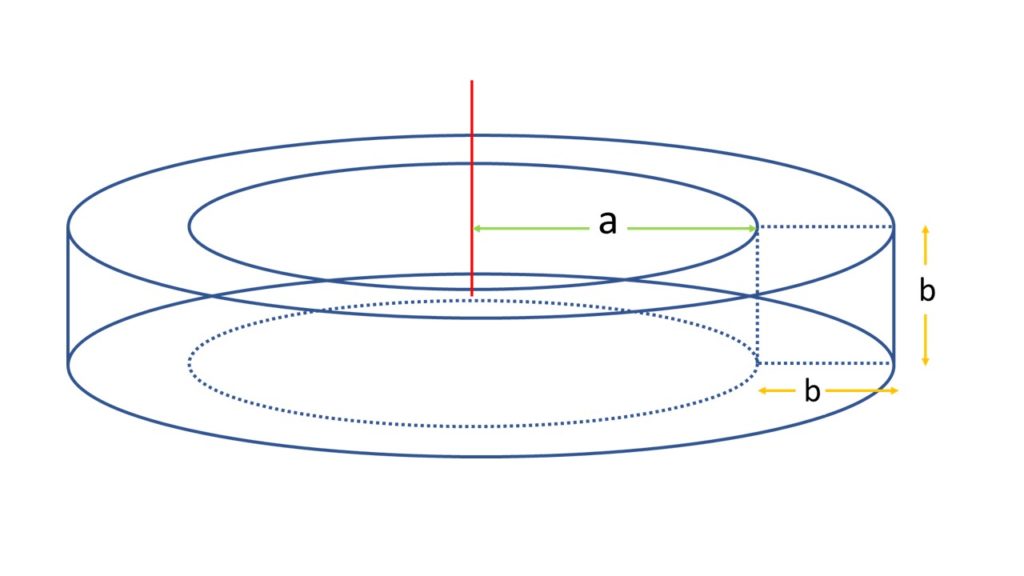
Se determinará la superficie usando la fórmula de la superficie para un toroide general. Con este fin es necesario saber la distancia del eje de rotación hasta el centroide del cuadrado, la cual, usando la nomenclatura anterior es R:
R = a + b/2
También es necesario conocer el perímetro L de la figura generatriz, que como en este caso se trata de un cuadrado de lado b, su contorno será de longitud:
L = 4⋅b
Luego se aplica la fórmula de la superficie de un toroide:
S = 2πR⋅L
Sustituyendo R y L por sus correspondientes expresiones, en función de las medidas a y b del toroide cuadrado se tiene:
S = 2π(a + b/2)⋅4⋅b = 8π(a + b/2)⋅b
Superficie del toroide cuadrado (suma de sus caras)
El toroide cuadrado de la figura anterior está constituido por cuatro caras: la superior y la inferior son aros planos, y la interior y exterior son cilíndricas.
Teniendo esto en cuenta, es posible calcular su superficie sumando el área de sus cuatro caras.
Las caras superior e inferior tienen un área igual a la del círculo exterior de radio (a+b) menos la del círculo interior de radio a, las cuales tienen como resultado:
Ss= Si= π[(a+b)2 – b2] = π⋅[a2+ 2ab]
La cara cilíndrica interna tiene área:
S1= 2πab
Y la cara cilíndrica externa tiene área:
S2= 2π(a+b)b = 2πab+2πb2
De modo que el área total del toroide será la suma Ss+Si+S1+S2:
A = 2π⋅[a2+ 2ab]+2πab + 2πab+2πb2.
