Reducción de términos semejantes: concepto, ejemplos y ejercicios

¿Qué es la reducción de términos semejantes?

La reducción de términos semejantes es un método que se emplea para simplificar expresiones algebraicas. En una expresión algebraica, los términos semejantes, son aquellos que tienen la misma variable; es decir, tienen las mismas incógnitas representadas por una letra, y estas tienen los mismos exponentes.

En algunos casos los polinomios son extensos, y para llegar a una solución se debe tratar de reducir la expresión; eso es posible cuando existen términos que son semejantes, que pueden ser combinados aplicando operaciones y propiedades algebraicas como suma, resta, multiplicación y división.

Explicación

Los términos semejantes están formados por las mismas variables con los mismos exponentes, y en algunos casos estos solo se diferencian por sus coeficientes numéricos.

También son considerados términos semejantes aquellos que no tienen variables; es decir, aquellos términos que solo poseen constantes. Así, por ejemplo, los siguientes son términos semejantes:

• 6x² – 3x². Ambos términos tienen la misma variable x².
• 4a²b³ + 2a²b³. Ambos términos tienen las mismas variables a²b³.
• 7 – 6. Los términos son constantes.

Aquellos términos que tienen las mismas variables, pero con diferentes exponentes son llamados términos no semejantes, como por ejemplo:

• 9a²b + 5ab. Las variables tienen diferentes exponentes.
• 5x + y. Las variables son diferentes.
• b – 8. Un término tiene una variable, el otro es una constante.

Identificando los términos semejantes que forman un polinomio, estos se pueden reducir a uno, combinando todos aquellos que tengan las mismas variables con iguales exponentes. De esa forma se simplifica la expresión disminuyendo el número de términos que la componen y se facilita el cálculo de su solución.

¿Cómo hacer una reducción de términos semejantes?

La reducción de términos semejantes se hace aplicando la propiedad asociativa de la adición y la propiedad distributiva del producto. Usando el siguiente procedimiento se puede hacer una reducción de términos:

• Primero se agrupan lo términos semejantes.
• Se suman o restan los coeficientes (los números que acompañan a las variables) de los términos semejantes, y se aplican las propiedades asociativas, conmutativas o distributivas, según sea el caso.
• Después se escriben los nuevos términos obtenidos, colocando delante de estos el signo que resultó de la operación.

Ejemplo

Reducir los términos de la siguiente expresión: 10x + 3y + 4x + 5y.

Solución

Primero se ordenan los términos para agrupar los que son semejantes, aplicando la propiedad conmutativa:

10x + 3y + 4x + 5y = 10x + 4x + 3y +5y.

Luego se aplica la propiedad distributiva y se suman los coeficientes que acompañan a las variables para obtener la reducción de los términos:

10x + 4x + 3y +5y

= (10 + 4)x + (3 + 5)y

= 14x + 8y.

Para reducir términos semejantes es importante tomar en cuenta los signos de que tienen los coeficientes que acompañan a la variable. Existen tres casos posibles:

Reducción de términos semejantes con signos iguales

En este caso los coeficientes son sumados y delante del resultado se coloca el signo de los términos. Por lo tanto, si son positivos, los términos resultantes serán positivos; en el caso de que los términos sean negativos, el resultado tendrá el signo (-) acompañado de la variable. Por ejemplo:

a) 22ab² + 12ab² = 34 ab².

b) -18x³ – 9x³ – 6 = -27x³ – 6.

Reducción de términos semejantes con signos diferentes

En este caso se restan los coeficientes, y delante del resultado se coloca el signo del coeficiente mayor. Por ejemplo:

a) 15x²y – 4x²y + 6x²y – 11x²y

= (15x²y + 6x²y ) + ( – 4x²y – 11x²y)

= 21x²y + (-15x²y)

= 21x²y – 15x²y

= 6x²y.

b) -5a³b + 3 a³b – 4a³b + a³b

= (3 a³b + a³b) + (-5a³b – 4a³b)

= 4a³b – 9a³b

= -5 a³b.

De esa forma, para reducir los términos semejantes que posean signos diferentes se forma un solo término aditivo con todos aquellos que tengan signo positivo (+), se suman los coeficientes y el resultado se acompaña de las variables.

De la misma manera se forma un término sustractivo, con todos aquellos términos que tengan signo negativo (-), se suman los coeficientes y el resultado se acompaña de las variables.

Finalmente se restan las sumas de los dos términos formados, y al resultado se coloca el signo de la mayor.

Reducción de términos semejantes en operaciones

La reducción de términos semejantes es una operación del álgebra, que puede ser aplicada en suma, resta, multiplicación y división algebraica.

En sumas

Cuando se tienen varios polinomios con términos semejantes, para reducirlos se ordenan los términos de cada polinomio manteniendo sus signos, luego se escriben unos tras otros y se reducen los términos semejantes. Por ejemplo, se tienen los siguientes polinomios:

3x – 4xy + 7x²y + 5xy².

– 6x²y – 2xy + 9 xy² – 8x.

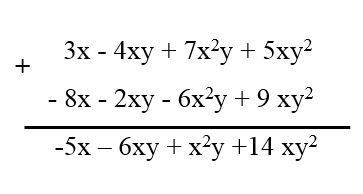
En restas

Para restar un polinomio de otro se escribe el minuendo y luego el sustraendo con sus signos cambiados, y después se hace la reducción de los términos semejantes. Por ejemplo:

5a³ – 3ab² + 3b²c

6ab² + 2a³ – 8b²c

Así, los polinomios son resumidos a 3a³ – 9ab² + 11b²c.

En multiplicaciones

En un producto de polinomios se multiplican los términos que conforman el multiplicando por cada término que forma el multiplicador, considerando que los signos de la multiplicación se mantienen iguales si estos son positivos.

Solo se cambiarán cuando se multiplique por un término que sea negativo; es decir, cuando dos términos del mismo signo se multiplican el resultado será positivo (+), y cuando tienen signos diferentes el resultado será negativo (-).

Por ejemplo:

a) (a + b) _* (a + b)

= a² + ab + ab + b²

= a² + 2ab+ b².

b) (a + b) _* (a – b)

= a² – ab + ab – b²

= a² – b².

c) (a – b) _* (a – b)

= a² – ab – ab + b²

= a² – 2ab+ b².

En divisiones

Cuando se quieren reducir dos polinomios a través de una división se debe encontrar un tercer polinomio que, al multiplicarse por el segundo (divisor), dé como resultado el primer polinomio (dividendo).

Para eso se deben ordenar los términos del dividendo y el divisor, de izquierda a derecha, de forma que las variables en ambos estén en el mismo orden.

Luego se realiza la división, comenzando desde el primer término de la izquierda del dividendo entre el primero de la izquierda del divisor, teniendo siempre en cuenta los signos de cada término.

Por ejemplo, reducir el polinomio: 10x⁴ – 48x³y + 51x²y² + 4xy³ – 15y⁴ dividiéndolo entre el polinomio: -5x² + 4xy + 3y².

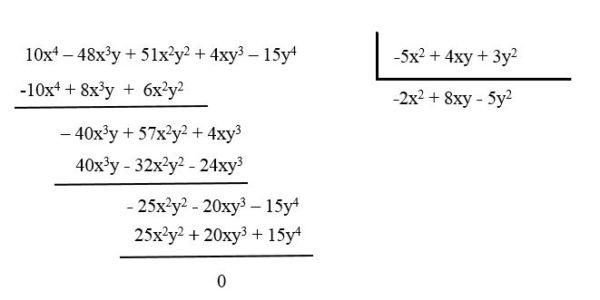
El polinomio resultante es -2x² + 8xy – 5y².

Ejercicios resueltos

Primer ejercicio

Reducir los términos de la expresión algebraica dada:

15a² – 8ab + 6a² – 6ab – 9 +4a² – 13 ab.

Solución

Se aplica la propiedad conmutativa de la suma, agrupando los términos que tengan las mismas variables:

15a² – 8ab + 6a² – 6ab + 9 +4a² – 13

= (15a² + 6a² + 4a²) + (– 8ab – 6ab) + (9 – 13).

Luego se aplica la propiedad distributiva de la multiplicación:

15a² – 8ab + 6a² – 6ab + 9 +4a² – 13

= (15 + 6 + 4) a² + (– 8 – 6) ab + (9 – 13).

Para finalizar, se simplifican sumando y restando los coeficientes de cada término:

15a² – 8ab + 6a² – 6ab + 9 +4a² – 13

= 25a² – 14ab – 4.

Segundo ejercicio

Simplificar el producto de los siguientes polinomios:

(8x³ + 7xy²)_*(8x³ – 7 xy²).

Solución

Se multiplica cada término del primer polinomio por el segundo, tomando en cuenta que los signos de los términos son diferentes; por lo tanto, el resultado de su multiplicación será negativo, así como también se deben aplicar las leyes de los exponentes.

(8x³ + 7xy²) _* (8x³ – 7xy²)

= 64 x⁶ – 56 x³_* xy² + 56 x³_* xy² – 49 x²y⁴

= 64 x⁶ – 49 x²y⁴.