Factorización: métodos, ejemplos y ejercicios resueltos

¿Qué es la factorización?

La factorización es un método a través del cual un polinomio se expresa en forma de multiplicación de factores, que pueden ser números, letras o ambos. Para factorizar se agrupan los factores que son comunes a los términos, y de esa forma se va descomponiendo el polinomio en varios polinomios.

Así, cuando los factores se multiplican entre sí el resultado es el polinomio original. La factorización es un método muy útil cuando se tienen expresiones algebraicas, porque se puede convertir en la multiplicación de varios términos sencillos; por ejemplo: 2a² + 2ab=2a _* (a + b).

Existen casos en los que un polinomio no puede ser factorizado porque no hay un factor común entre sus términos; así, esas expresiones algebraicas son divisibles solamente entre ellas mismas y por 1. Por ejemplo: x + y + z.

En una expresión algebraica el factor común es el máximo común divisor de los términos que la componen.

Métodos de factorización

Hay varios métodos de factorización, que son aplicados dependiendo el caso. Algunos de estos son los siguientes:

Factorización por factor común

En este método se identifican aquellos factores que son comunes; es decir, aquellos que están repetidos en los términos de la expresión. Luego se aplica la propiedad distributiva, se saca el máximo común divisor y se completa la factorización.

En otras palabras, se identifica el factor común de la expresión y se divide cada término entre este; los términos resultantes serán multiplicados por el máximo común divisor para expresar la factorización.

Ejemplo 1

Factorizar (b²x) + (b²y).

Solución

Primero se encuentra el factor común de cada término, que en este caso es b², y luego se dividen los términos entre el factor común de la siguiente manera:

(b²x) / b² = x

(b²y) / b² = y.

Se expresa la factorización, multiplicando el factor común por los términos resultantes:

(b²x) + (b²y) = b² (x + y).

Ejemplo 2

Factorizar (2a²b³) + (3ab²).

Solución

En este caso tenemos dos factores que se repiten en cada término que son “a” y “b”, y que se encuentran elevados a una potencia. Para factorizarlos primero se descomponen los dos términos en su forma larga:

2_*a_*a_*b_*b_*b + 3a_*b_*b

Puede observarse que el factor “a” se repite una sola vez en el segundo término, y el factor “b” se repite dos veces en este; así que en el primer término solo queda el 2, un factor “a” y uno “b”; mientras que en el segundo término solo queda el 3.

Por lo tanto, se escribe las veces que “a” y “b” se repiten y se multiplica por los factores que sobran de cada término, como se observa en la imagen:

Factorización por agrupamiento

Como no en todos los casos el máximo común divisor de un polinomio se encuentra claramente expresado, es necesario hacer otros pasos para poder reescribir el polinomio y así factorizar.

Uno de esos pasos consiste en agrupar los términos del polinomio en varios grupos, para luego usar el método del factor común.

Ejemplo 1

Factorizar ac + bc + ad + bd.

Solución

Se tienen 4 factores donde dos son comunes: en el primer término es “c” y en el segundo es “d”. De esa manera se agrupan y separan los dos términos:

(ac + bc) + (ad + bd).

Ahora es posible aplicar el método del factor común, dividiendo cada término por su factor común y luego multiplicando ese factor común por los términos resultantes, así:

(ac + bc) / c = a + b

(ad + bd) / d = a + b

c(a + b) + d(a + b).

Ahora se obtiene un binomio que es común para ambos términos. Para factorizarlo se multiplica por los factores restantes; de esa manera se tiene que:

ac + bc + ad + bd =  (c + d) _* (a + b).

Factorización por inspección

Este método se usa para factorizar polinomios cuadráticos, también llamados trinomios; es decir, aquellos que se estructuran como ax² ± bx + c, donde el valor de “a” es diferente de 1. Este método también se usa cuando el trinomio tiene la forma x² ± bx + c y el valor del “a” = 1.

Ejemplo 1

Factorizar x² + 5x + 6.

Solución

Se tiene un trinomio cuadrático de la forma x² ± bx + c. Para factorizarlo primero se deben encontrar dos números que, al multiplicarse, den como resultado el valor de “c” (es decir, 6) y que su suma sea igual al coeficiente “b”, que es 5. Esos números son 2 y 3:

2 _* 3 = 6

2 + 3 = 5.

De esa forma, la expresión se simplifica así:

(x² + 2x) + (3x + 6)

Se factoriza cada término:

• Para (x² + 2x) se saca el término común: x (x + 2)
• Para (3x + 6) = 3(x + 2)

Así, la expresión queda:

x(x +2) + 3(x +2).

Como se tiene un binomio en común, para reducir la expresión se multiplica este por los términos sobrantes y se tiene que:

x² + 5x + 6 = (x + 2) _* (x + 3).

Ejemplo 2

Factorizar 4a² + 12a +9=0.

Solución

Se tiene un trinomio cuadrático de la forma ax² ± bx + c y para factorizarlo se multiplica toda la expresión por el coeficiente de x²; en este caso, 4.

4a² + 12a +9 = 0

4a² (4) + 12a(4) + 9(4)=0 (4)

16 a² + 12a(4) + 36 = 0

4² a² + 12a(4) + 36 = 0

Ahora se deben hallar dos números que, cuando se multipliquen entre sí, den como resultado el valor de “c” (que es 36) y que al sumarse den como resultado el coeficiente del término “a”, que es 6.

6 _* 6 = 36

6 + 6 = 12.

De esa manera se rescribe la expresión, teniendo en cuenta de que 4² a² = 4a _* 4a. Por lo tanto, se aplica la propiedad distributiva para cada término:

(4a + 6) _* (4a + 6).

Por último, se divide la expresión por el coeficiente de a²; es decir, 4:

(4a + 6) _* (4a + 6) / 4 = ((4a + 6)/ 2) _* ((4a + 6)/ 2).

La expresión queda de la siguiente manera:

4a² + 12a +9 = (2a +3) _* (2a + 3).

Factorización con productos notables

Existen casos en los que, para factorizar completamente los polinomios con los métodos anteriores, se convierte en un proceso muy largo.

Es por eso que una expresión puede ser desarrollada con las fórmulas de los productos notables y así el proceso se hace más simple. Entre los productos notables más usados están:

• Diferencia de dos cuadrados: (a² – b²) = (a – b) _* (a + b)
• Cuadrado perfecto de una suma: a² + 2ab +b² = (a + b)²
• Cuadrado perfecto de una diferencia: a² – 2ab + b² = (a – b)²
• Diferencia de dos cubos: a³ – b³ = (a-b)_*(a² + ab + b²)
• Suma de dos cubos: a³ – b³ = (a + b) _* (a² – ab + b²)

Ejemplo 1

Factorizar (5² – x²)

Solución

En este caso se tiene una diferencia de dos cuadrados; por lo tanto, se aplica la fórmula del producto notable:

(a² – b²) = (a – b) _* (a + b)

(5² – x²) = (5 – x) _* (5 + x)

Ejemplo 2

Factorizar 16x² + 40x + 25²

Solución

En este caso se tiene un cuadrado perfecto de una suma, porque se pueden identificar dos términos elevados al cuadrado, y el término que sobra es el resultado de multiplicar dos por la raíz cuadrada del primer término, por la raíz cuadrada del segundo término.

a² + 2ab +b² = (a + b)²

Para factorizar solo se calculan las raíces cuadradas del primer y tercer término:

√(16x²)= 4x

√(25²) = 5.

Luego se expresan los dos términos resultantes separados por el signo de la operación, y se eleva todo el polinomio al cuadrado:

16x² + 40x + 25² = (4x + 5)².

Ejemplo 3

Factorizar 27a³ – b³

Solución

La expresión representa una resta en la que dos factores están elevados al cubo. Para factorizarlos se aplica la fórmula del producto notable de la diferencia de cubos, que es:

a³ – b³ = (a-b)_*(a² + ab + b²)

Así, para factorizar se saca la raíz cúbica de cada término del binomio y se multiplica por el cuadrado del primer término, más el producto del primer por el segundo término, más el segundo término al cuadrado.

27a³ – b³

³√(27a³)= 3a

³√(-b³)= -b

27a³ – b³ = (3a – b) _* [ (3a)² + 3ab + b²) ]

27a³ – b³ = (3a – b) _* (9a² + 3ab + b²)

Factorización con la regla de Ruffini

Este método es usado cuando se tiene un polinomio de grado mayor a dos, para así simplificar la expresión a varios polinomios de menor grado.

Ejemplo 1

Factorice Q(x) = x⁴ – 9x² + 4x + 12

Solución

Primero se buscan los números que sean divisores de 12, que es el término independiente; estos son ±1, ±2, ±3, ±4, ±6 y ±12.

Luego se sustituye la x por estos valores, de menor a mayor, y así se determina con cuál de los valores la división será exacta; es decir, que el resto debe ser 0:

x = -1

Q (-1) = (-1)⁴ – 9(-1)² + 4(-1) + 12 = 0.

x = 1

Q (1) = 1⁴ – 9(1)² + 4(1) + 12 = 8  ≠ 0.

x = 2

Q (2) = 2⁴ – 9(2)² + 4(2) + 12 = 0.

Y así sucesivamente para cada divisor. En este caso, los factores encontrados son para x = -1 y x = 2.

Ahora se aplica el método de Ruffini, según el cual los coeficientes de la expresión serán divididos entre los factores encontrados para que la división sea exacta. Los términos de polinomio son ordenados de mayor a menor exponente; en el caso que falte un término con el grado que sigue en la secuencia, se coloca un 0 en su lugar.

Los coeficientes se ubican en un esquema como se observa en la siguiente imagen.

Se baja el primer coeficiente y se multiplica por el divisor. En este caso, el primer divisor es -1, y el resultado se coloca en la siguiente columna. Luego se suma en vertical el valor del coeficiente con ese resultado que se obtuvo y el resultado se coloca debajo. De esa manera se repite el proceso hasta la última columna.

Luego se repite nuevamente el mismo procedimiento, pero con el segundo divisor (que es 2) porque aún se puede simplificar la expresión.

Así, para cada raíz conseguida el polinomio tendrá un término (x – a), donde “a” es el valor de la raíz:

(x – (-1)) _* (x – 2) = (x + 1) _* (x – 2)

Por otra parte, se deben multiplicar estos términos por el resto que quedó de la regla de Ruffini 1: 1 y -6, que son factores que representan un grado. De esa forma la expresión que se forma es: (x² + x – 6).

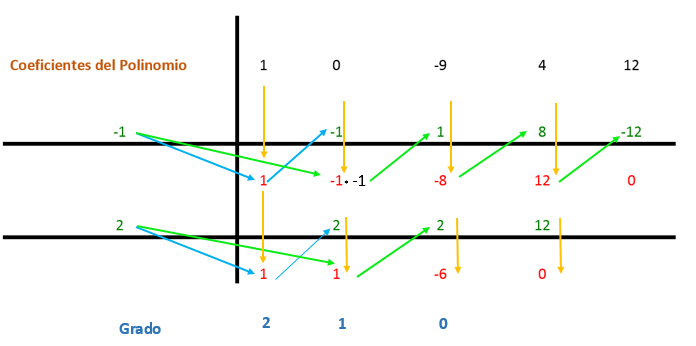
La obtención del resultado de la factorización del polinomio por el método de Ruffini es:

x⁴ – 9x² + 4x + 12 = (x + 1) _* (x – 2) _* (x² + x – 6)

Para terminar, el polinomio de grado 2 que aparece en la expresión anterior se puede reescribir como (x+3)(x-2). Por lo tanto, la factorización final es:

x⁴ – 9x² + 4x + 12 = (x + 1) _* (x – 2)_*(x+3)_*(x-2).

Referencias

1. Arthur Goodman, L. H. (1996). Algebra y trigonometría con geometría analítica. Pearson Educación.
2. J, V. (2014). How to Teach Kids About Factoring a Polynomial.
3. Manuel Morillo, A. S. (s.f.). Matemática Básica Con Aplicaciones.
4. Roelse, P. L. (1997). Linear methods for polynomial factorization over finite fields: theory and implementations. Universität Essen.
5. Sharpe, D. (1987). Rings and Factorization.