Cuasivarianza: fórmula y ecuaciones, ejemplos, ejercicio
La cuasivarianza, cuasi varianza o varianza insesgada es una medida estadística de la dispersión de los datos de una muestra respecto a la media. La muestra a su vez, consiste en una serie de datos tomados de un universo mayor, llamado población.
Se denota de varias maneras, aquí se ha elegido sc2 y para calcularla se sigue la siguiente fórmula:

Donde:
-sc2 = la cuasivarianza o varianza de la muestra (varianza muestral)
-xi = cada uno de los datos de la muestra
-n = número de observaciones
-X = la media de la muestra
Dado que la unidad de la cuasivarianza muestral es el cuadrado de la unidad en que viene la muestra, al momento de interpretar los resultados se prefiere trabajar con la cuasi desviación típica o desviación estándar de la muestra.
Esta se denota como scy se obtiene extrayendo la raíz cuadrada de la cuasivarianza:
sc = √ sc2
La cuasivarianza es similar a la varianza s2, con la única diferencia de que en el denominador de aquella está n-1, mientras que en el de la varianza se divide solamente por n. Es evidente que cuando n es muy grande, los valores de ambas tienden a ser los mismos.
Cuando se conoce el valor de la cuasivarianza, de inmediato se puede conocer el de la varianza.
Índice del artículo
Con frecuencia se desea conocer las características de una población cualquiera: de personas, animales, plantas y en general cualquier tipo de objetos. Pero analizar la población entera puede no ser tarea fácil, sobre todo si el número de elementos es muy grande.
Entonces se toman muestras, con la esperanza de que el comportamiento de ellas refleje al de la población y así poder realizar inferencias sobre la misma, gracias a las cuales se optimizan los recursos. A esto se le conoce como inferencia estadística.
He aquí algunos ejemplos en los cuales la cuasivarianza y la cuasi desviación típica asociada, sirven como indicador estadístico al señalar que tanto se alejan los resultados obtenidos con respecto a la media.
1.- El director de mercadeo de una compañía que fabrica baterías para automóviles necesita estimar, en meses, la duración promedio de una batería.
Para ello selecciona aleatoriamente una muestra de 100 baterías de esa marca compradas. La compañía conserva un registro de los datos de los compradores y puede entrevistarlos para conocer la duración de las baterías.

2.- La dirección académica de una institución universitaria necesita estimar la matrícula del siguiente año, analizando la cantidad de estudiantes que se espera que aprueben las asignaturas que cursan actualmente.
Por ejemplo, de cada una de las secciones que actualmente cursan la asignatura Física I, la dirección puede seleccionar una muestra de estudiantes y analizar su rendimiento en dicha cátedra. De esta forma puede inferir cuántos estudiantes cursarán Física II en el próximo período.
3.- Un grupo de astrónomos enfoca su atención en una parte del cielo, donde se observan cierto número de estrellas con determinadas características: tamaño, masa y temperatura por ejemplo.
Cabe preguntarse si las estrellas en otra región similar tendrán esas mismas características, incluso estrellas en otras galaxias, como las vecinas Nubes de Magallanes o Andrómeda.
En la cuasivarianza se divide entre n-1 en vez de hacerlo entre n y se debe a que la cuasivarianza es un estimador insesgado, como se dijo al comienzo.
Sucede que de una misma población es posible extraer muchas muestras. La varianza de cada una de estas muestras también se puede promediar, pero el promedio de estas varianzas no resulta ser igual a la varianza de la población.
De hecho, el promedio de las varianzas de la muestra tiende a subestimar la varianza de la población, a menos que se utilice n-1 en el denominador. Se puede comprobar que el valor esperado de la cuasivarianza E(sc2) es precisamente s2.
Por ello se dice que la cuasivarianza es insesgada y resulta un mejor estimador de la varianza poblacional s2.
Se demuestra fácilmente que la cuasivarianza también se puede calcular del siguiente modo:
sc2 = [∑x2 / (n-1)] – [∑nX2 / (n-1)]
Al tener la desviación de la muestra, podemos saber cuántas desviaciones estándar tiene un valor particular x, ya sea por encima o por debajo de la media.
Para ello se emplea la siguiente expresión adimensional:
Puntuación estándar = (x – X) / sc
Calcular la cuasivarianza y la cuasi desviación típica de los siguientes datos, que consisten en pagos mensuales en $ hechos por una compañía de seguros a una clínica privada.
863 903 957 1041 1138 1204 1354 1624 1698 1745 1802 1883
a) Use la definición de cuasivarianza dada al comienzo y también verifique el resultado mediante la forma alternativa dada en la sección precedente.
b) Calcule la puntuación estándar del segundo dato, leyendo de arriba hacia abajo.
El problema se puede resolver a mano con ayuda de una calculadora sencilla o científica, para lo cual hay que proceder en orden. Y para ello nada mejor que organizar los datos en una tabla como la que se muestra a continuación:
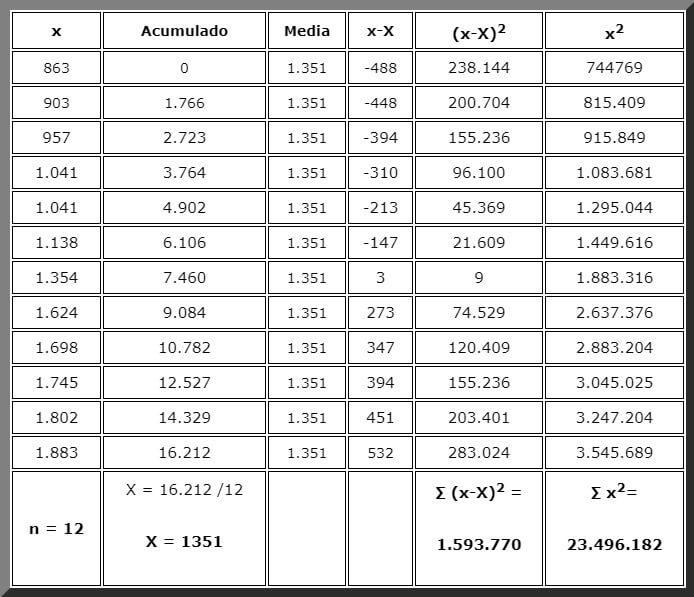
Gracias a la tabla se tiene la información organizada y las cantidades que se van a necesitar en las fórmulas están al final de las respectivas columnas, listas para usar de inmediato. Las sumatorias se indican en negritas.
La columna de la media se repite siempre, pero vale la pena pues es conveniente tener a la vista el valor, para ir llenando cada fila de la tabla.
Finalmente se aplica la ecuación para la cuasivarianza dada al comienzo, solamente se sustituyen los valores y en cuanto a la sumatoria, ya la tenemos calculada:
sc2 = 1.593.770 / (12-1) = 1.593.770 / 11 = 144.888,2
Este es el valor de la cuasivarianza y sus unidades son “dólares al cuadrado”, lo que no tiene mucho sentido práctico, por eso se calcula la cuasidesviación estándar de la muestra, que no es más que la raíz cuadrada de la cuasivarianza:
sc = (√144.888,2) $ = 380,64 $
De inmediato se corrobora que este valor se obtiene igualmente con la forma alternativa de la cuasivarianza. La sumatoria necesaria está al final de la última columna de la izquierda:
sc2 = [∑x2 / (n-)] – [∑nX2 / (n-1)]= [23.496.182/ 11] – [12 x 13512/ 11]
= 2.136.016,55 – 1.991.128,36 = 144.888 dólares al cuadrado
Es el mismo valor obtenido con la fórmula dada al comienzo.
El segundo valor de arriba abajo es 903, su puntuación estándar es
Puntuación estándar de 903 = (x – X) / sc = (903 – 1351)/380.64 = -1.177
- Canavos, G. 1988. Probabilidad y Estadística: Aplicaciones y métodos. McGraw Hill.
- Devore, J. 2012. Probability and Statistics for Engineering and Science. 8th. Edition. Cengage.
- Levin, R. 1988. Estadística para Administradores. 2da. Edición. Prentice Hall.
- Medidas de dispersión. Recuperado de: thales.cica.es.
- Walpole, R. 2007. Probabilidad y Estadística para Ingeniería y Ciencias. Pearson.
