Papomudas: qué es, cómo resolverlo, ejemplos, ejercicios

¿Qué es el papomudas?

El papomudas es un procedimiento de resolución de expresiones algebraicas. Sus siglas indican el orden de prioridad de las operaciones: paréntesis, potencias, multiplicación, división, adición y sustracción. Usando esta palabra se puede recordar fácilmente el orden en el que se debe resolver una expresión compuesta por varias operaciones.

Generalmente, en las expresiones numéricas se pueden encontrar varias operaciones aritméticas juntas, como sumas, restas, multiplicaciones y divisiones, que además pueden ser de fracciones, potencias y raíces. Para resolverlas se hace necesario seguir un procedimiento que garantiza que los resultados estarán correctos.

Una expresión aritmética que se compone de una combinación de esas operaciones debe resolverse según la prioridad de orden, también conocida como jerarquía de las operaciones, establecida hace mucho tiempo en convenciones universales. Así, todas las personas pueden seguir el mismo procedimiento y obtener el mismo resultado.

Características

El papomudas es procedimiento estándar que establece cuál es el orden que debe ser seguido cuando se debe dar solución a una expresión, que está compuesta por una combinación de operaciones como suma resta, multiplicación y división.

Con este procedimiento se establece el orden de prioridad de una operación con relación a las otras en el momento en que serán resultas; es decir, cada operación tiene un turno o nivel jerárquico para ser resuelta.

El orden en que deben resolverse las diferentes operaciones de una expresión es dado por cada sigla de la palabra papomudas. De esa forma, se tiene que:

1. Pa: paréntesis, corchetes o llaves.
2. Po: potencias y raíces.
3. Mu: multiplicaciones.
4. D: divisiones.
5. A: adiciones o sumas.
6. S: sustracciones o restas.

Este procedimiento también es llamado en inglés como PEMDAS; para recordar fácilmente esta palabra es asociada a la frase: “Please Excuse My Dear Aunt Sally”, donde cada letra inicial corresponde a una operación aritmética, de la misma manera que el papomudas.

¿Cómo resolverlos?

Basado en la jerarquía que establece el papomudas para resolver las operaciones de una expresión, es necesario cumplir el siguiente orden:

• Primero se deben resolver todas las operaciones que estén dentro de símbolos de agrupación, como paréntesis, llaves, corchetes y barras de fracción. Cuando existen símbolos de agrupación dentro de otros, se debe comenzar a calcular de adentro hacia afuera.

Estos símbolos son usados para cambiar el orden en que se resuelven las operaciones, porque siempre se debe resolver primero lo que este dentro de estos.

• Luego se resuelven las potencias y las raíces.
• En tercer lugar se resuelven las multiplicaciones y divisiones. Estas tienen el mismo orden de prioridad; por eso, cuando en una expresión se encuentren estas dos operaciones, se debe resolver la que aparezca primero, leyendo la expresión de izquierda a derecha.
• En último lugar se resuelven las sumas y restas, que también tienen un mismo orden de prioridad y, por lo tanto, es resuelta la que aparezca primero en la expresión, leída de izquierda a derecha.
• Nunca se deben mezclar las operaciones al ser leídas de izquierda a derecha, siempre se debe seguir el orden de prioridad o jerarquía establecido por el papomudas.

Es importante recordar que el resultado de cada operación se debe colocar en el mismo orden con relación a los demás, y todos los pasos intermedios deben estar separados por un signo hasta llegar al resultado final.

Aplicación

El procedimiento papomudas es usado cuando se tiene una combinación de diferentes operaciones. Teniendo en cuenta cómo se resuelven, este puede ser aplicado en:

Expresiones que contienen sumas y restas

Es una de las operaciones más simples, porque ambas tienen el mismo orden de prioridad, de tal forma que se debe resolver comenzando desde la izquierda hacia la derecha en la expresión; por ejemplo:

22 -15 + 8 +6 = 21.

Expresiones que contienen sumas, restas y multiplicaciones

En este caso la operación de mayor prioridad es la multiplicación, luego se resuelven las sumas y restas (la que este primero en la expresión). Por ejemplo:

6 _* 4 – 10 + 8 _* 6 – 16 + 10 _* 6

= 24 -10 + 48 – 16 + 60

= 106.

Expresiones que contienen suma, resta multiplicación y división

En este caso se tiene una combinación de todas las operaciones. Se comienza por resolver la multiplicación y división que tienen prioridad superior, luego las sumas y restas. Leyendo la expresión de izquierda a derecha, se resuelve según su jerarquía y posición dentro de la expresión; por ejemplo:

7 + 10 _* 13 – 8 + 40 ÷ 2

= 7 + 130 – 8 + 20

= 149.

Expresiones que contienen suma, resta, multiplicación, división y potencias

En este caso uno de los números se encuentra elevado a una potencia, que dentro del nivel de prioridad debe ser resuelta primero, para después resolver las multiplicaciones y divisiones, y por último las sumas y restas:

4 + 4² _* 12 – 5 + 90 ÷ 3

= 4 + 16 _* 12 – 5 + 90 ÷ 3

= 4 + 192 – 5 + 30

= 221.

Al igual que las potencias, las raíces también tienen el segundo orden de prioridad; por eso, en expresiones que las contengan deben resolverse primero que las multiplicaciones, divisiones, sumas y restas:

5 _* 8 + 20 ÷ √16

= 5 _* 8 + 20 ÷ 4

= 40 + 5

= 45.

Expresiones que utilizan símbolos de agrupación

Cuando son usados signos como paréntesis, llaves, corchetes y barras de fracciones, lo que está dentro de estos se resuelve primero, sin importar el orden de prioridad de las operaciones que este contenga con relación a los que están fuera de este, como si se tratara de una expresión aparte:

14 ÷ 2 – (8 – 5)

= 14 ÷ 2 – 3

= 7 – 3

= 4.

Si dentro de este se encuentran varias operaciones, estas deben resolverse por orden jerárquico. Luego se resuelven las demás operaciones que componen la expresión; por ejemplo:

2 + 9 * (5 + 2³ – 24 ÷ 6) – 1

= 2 + 9 * (5 + 8 – 4) – 1

= 2 + 9 * 9 – 1

= 2 + 81 – 1

= 82.

En algunas expresiones se utilizan símbolos de agrupación dentro de otros, como cuando es necesario cambiar el signo de una operación. En esos casos se debe comenzar resolviendo de adentro hacia afuera; es decir, simplificando los símbolos de agrupación que estén en el centro de una expresión.

Generalmente, el orden para solucionar operaciones contenidas dentro de estos símbolos es: primero resolver lo que está dentro de paréntesis ( ), luego corchetes [ ] y por último las llaves {}.

90 – 3_*[12 + (5_*4) – (4_*2)]

= 90 – 3_* [12 + 20 – 8]

= 90 – 3 _* 24

= 90 – 72

= 18.

Ejercicios

Primer ejercicio

Hallar el valor de la siguiente expresión:

20² + √225 – 155 + 130.

Solución

Aplicando el papomudas, se tienen que resolver en primer lugar las potencias y raíces, y luego sumas y restas. En este caso, las dos primeras operaciones pertenecen al mismo orden, por eso se resuelve la que esté primero, comenzando de izquierda a derecha:

20² + √225 – 155 + 130

= 400 + 15 -155 + 130.

Luego sumas y restas, comenzando por la izquierda también:

400 + 15 -155 + 130

= 390.

Segundo ejercicio

Hallar el valor de la siguiente expresión:

[- (6³ – 3⁶) ÷ (8 _* 6 ÷16)].

Solución

Se comienza por resolver las operaciones que están dentro de los paréntesis, siguiendo el orden jerárquico que estas poseen según el papomudas.

Primero se resuelven las potencias del primer paréntesis, luego se resuelven las operaciones del segundo paréntesis. Como pertenecen al mismo orden, se resuelve la primera operación de la expresión:

[- (6³ – 3⁶) ÷ (8 _* 6 ÷16)]

= [- (216 – 729) ÷ (8 _* 6 ÷16)]

= [- (216 – 729) ÷ (48 ÷16)]

= [- (-513) ÷ (3)].

Como ya fueron resueltas las operaciones dentro de los paréntesis, ahora se continúa con la división que tiene mayor jerarquía que la resta:

[- (-513) ÷ (3)] = [- (-171)].

Para finalizar, el paréntesis que separa el signo menos (-) del resultado, que en este caso es negativo, indica que se debe hacer una multiplicación de estos signos. Así, el resultado de la expresión es:

[- (-171)] = 171.

Tercer ejercicio

Hallar el valor de la siguiente expresión:

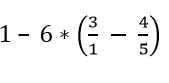
Solución

Se comienza resolviendo las fracciones que están dentro del paréntesis:

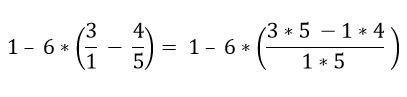
Dentro del paréntesis se tienen varias operaciones. Se resuelven primero las multiplicaciones y luego las restas; en este caso la barra de la fracción es considerada como un símbolo de agrupación y no como una división, por eso deben resolverse las operaciones de la parte superior e inferior:

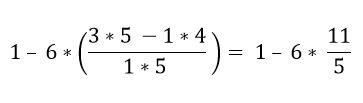
Por orden jerárquico, debe ser resuelta la multiplicación:

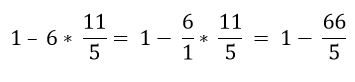
Para finalizar, se resuelve la sustracción: