Ortoedro: fórmulas, área, volumen, diagonal, ejemplos
El ortoedro es una figura geométrica volumétrica o tridimensional que se caracteriza por tener seis caras rectangulares, de modo que las caras opuestas están en planos paralelos y son rectángulos idénticos o congruentes entre sí. Por otra parte, las caras adyacentes a una cara dada están en planos perpendiculares al de la cara inicial.
También puede considerarse al ortoedro como un prisma ortogonal de base rectangular, en el cual los ángulos diedros formados por los planos de dos caras adyacentes a una arista común, miden 90º. El ángulo diedro entre dos caras se mide sobre la intersección de las caras con un plano perpendicular y común a las mismas.
Asimismo, el ortoedro es un paralelepípedo rectángulo, ya que así se define al paralelepípedo como la figura volumétrica de seis caras, las cuales son paralelas dos a dos.
En un paralelepípedo cualquiera la caras son paralelogramos, pero en el paralelepípedo rectángulo las caras tienen que ser rectangulares.
Índice del artículo
Las partes de un poliedro, como el ortoedro, son:
-Aristas
-Vértices
-Caras
El ángulo entre dos aristas de una cara del ortoedro coincide con el ángulo diedro formado por sus otras dos caras adyacentes a cada una de las aristas, formando ángulo recto. La siguiente imagen aclara cada concepto:
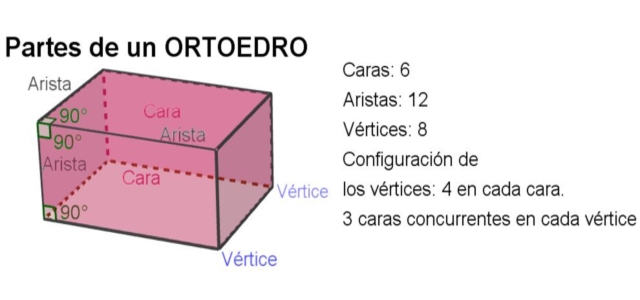
-En total un ortoedro tiene 6 caras, 12 aristas y 8 vértices.
-El ángulo entre dos aristas cualquiera es un ángulo recto.
-El ángulo diedro entre dos caras cualesquiera también es recto.
-En cada cara hay cuatro vértices y en cada vértice concurren tres caras mutuamente ortogonales.
La superficie o área de un ortoedro es la suma de las áreas de sus caras.
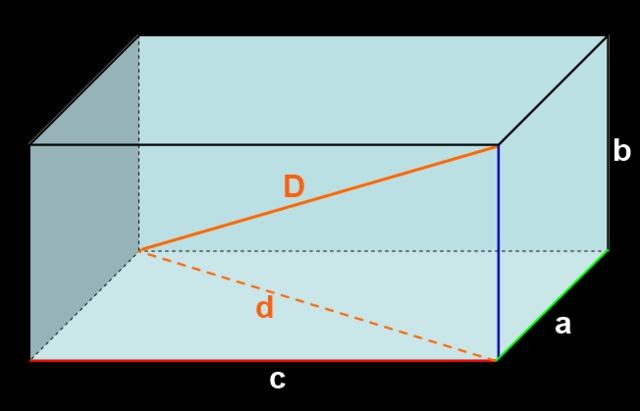
Si las tres aristas que concurren en un vértice tienen medidas a, b y c, tal como se muestra en la figura 3, entonces la cara frontal tiene área c⋅b y la cara del fondo también tiene área c⋅b.
Luego, las dos caras laterales tienen área a⋅b cada una. Y por último, las caras del piso y del techo tienen área a⋅c cada una.
Sumando el área de todas las caras se obtiene:
A = 2⋅c⋅b + 2⋅a⋅b + 2⋅a⋅c
Sacando factor común y ordenando los términos:
A = 2⋅( a⋅b + b⋅c + c⋅a )
Si se piensa al ortoedro como un prisma, entonces su volumen se calcula así:
Volumen = Área de la base del prisma x la altura del prisma
En este caso se toma como base rectangular el piso de dimensiones c y a, entonces el área de la base es c⋅a.
La altura viene dada por la longitud b de las aristas ortogonales a las caras de lados a y c.
Multiplicando el área de la base (a⋅c) por la altura b se tiene el volumen V del ortoedro:
V = a⋅b⋅c
En un ortoedro hay dos clases de diagonales: las diagonales externas y las diagonales internas.
Las diagonales externas están sobre las caras rectangulares, mientras que las diagonales internas son los segmentos que unen dos vértices opuestos, entendiéndose por vértices opuestos los que no comparten ninguna arista.
En un ortoedro hay cuatro diagonales internas, todas de igual medida. La longitud de las diagonales internas puede obtenerse de aplicar el teorema de Pitágoras para triángulos rectángulos.
La longitud d de la diagonal externa de la cara del piso del ortoedro cumple la relación pitagórica:
d2 = a2 + c2
Similarmente, la diagonal interior de medida D cumple la relación pitagórica:
D2 = d2 + b2.
Combinando las dos expresiones anteriores se tiene:
D2 = a2 + c2 + b2.
Finalmente la longitud de cualquiera de las diagonales internas del ortoedro está dada por la siguiente fórmula:
D = √( a2 + b2 + c2 ).
Un albañil construye un tanque en forma de ortoedro cuyas dimensiones internas son: 6 m x 4 m de base y 2 m de altura. Se pide:
a) Determinar la superficie interior del tanque si el mismo está completamente abierto en su parte superior.
b) Calcular el volumen del espacio interior del tanque.
c) Hallar la longitud de una diagonal interior.
d) ¿Cuál es la capacidad del tanque en litros?
Solución a
Tomaremos las dimensiones de la base rectangular a = 4 m y c = 6 m y la altura como b = 2 m
El área de un ortoedro con las dimensiones dadas está dada por la siguiente relación:
A = 2⋅(a⋅b + b⋅c + c⋅a) = 2⋅(4 m⋅2 m + 2 m⋅6 m + 6 m⋅4 m)
Es decir:
A = 2⋅(8 m2 + 12 m2 + 24 m2) = 2⋅(44 m2) = 88 m2
El resultado anterior es el área del ortoedro cerrado con las dimensiones dadas, pero como se trata de un tanque completamente descubierto en su parte superior, para obtener la superficie de las paredes interiores del tanque debe restarse el área de la tapa faltante que es:
c⋅a = 6 m ⋅ 4 m = 24 m2.
Finalmente, la superficie interior del tanque será: S = 88 m2 – 24 m2 = 64 m2.
Solución b
El volumen interior del tanque viene dado por el volumen de un ortoedro de las dimensiones interiores del tanque:
V = a⋅b⋅c = 4 m ⋅ 2 m ⋅ 6 m = 48 m3.
Solución c
La diagonal interior de un octaedro con las dimensiones del interior del tanque tiene una longitud D dada por:
√( a2 + b2 + c2 ) = √( (4 m)2 + (2 m)2 + (6 m)2 )
Efectuando las operaciones indicadas nos queda:
D = √( 16 m2 + 4 m2 + 36 m2 ) = √(56 m2) = 2√(14) m = 7,48 m.
Solución d
Para calcular la capacidad del tanque en litros, es necesario saber que el volumen de un decímetro cúbico equivale a la capacidad de un litro. Previamente se había calculado en volumen en metros cúbicos, pero ha de transformarse a decímetros cúbicos y luego a litros:
V = 48 m3 = 48 (10 dm)3 = 4.800 dm3 = 4.800 L
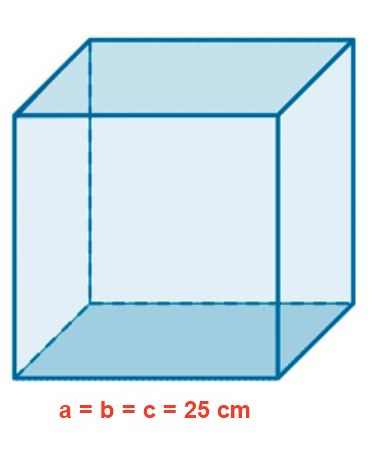
Un acuario de vidrio tiene forma cúbica de 25 cm de lado. Determinar el área en m2, el volumen en litros y la longitud de una diagonal interior en cm.
Solución
El área se calcula mediante la misma fórmula del ortoedro, pero tomando en cuenta que todas las dimensiones son idénticas:
A = 2⋅( 3 a⋅a ) = 6⋅ a2 = 6⋅ (25 cm)2 = 1.250 cm2
El volumen del cubo está dado por:
V = a3 = (25 cm)3 = 15.625 cm3 = 15.625 (0,1 dm)3 = 15,625 dm3 = 15,625 L.
La longitud D de la diagonal interior es:
D = √( 3a2) = 25√(3) cm = 43,30 cm.
- Arias J. GeoGebra: Prisma. Recuperado de: youtube.com.
- Cálculo.cc. Ejercicios y problemas resueltos de áreas y volúmenes. Recuperado de: calculo.cc.
- Salvador R. Pirámide + ortoedro con GEOGEBRA (IHM). Recuperado de: youtube.com
- Weisstein, Eric. “Ortoedro”. MathWorld. Wolfram Research.
- Wikipedia. Ortoedro. Recuperado de: es.wikipedia.com
