Proceso adiabático: tipos, ejemplos, ejercicios resueltos
Un proceso adiabático es aquel donde no existe intercambio de calor entre el sistema y sus alrededores, ya sea porque ocurre dentro de un medio aislante, o porque transcurre a gran rapidez. Esto significa que en los alrededores del sistema, este es, la porción del universo bajo estudio, no debe percibirse cambios de temperatura, sino solo trabajo.
Se trata de uno de los procesos elementales de la termodinámica. A diferencia de los otros procesos (isocóricos, isobáricos e isotérmicos), ninguna de sus variables físicas permanece constante; es decir, las magnitudes de la presión, el volumen, la temperatura y la entropía cambian a medida que el proceso adiabático evoluciona.
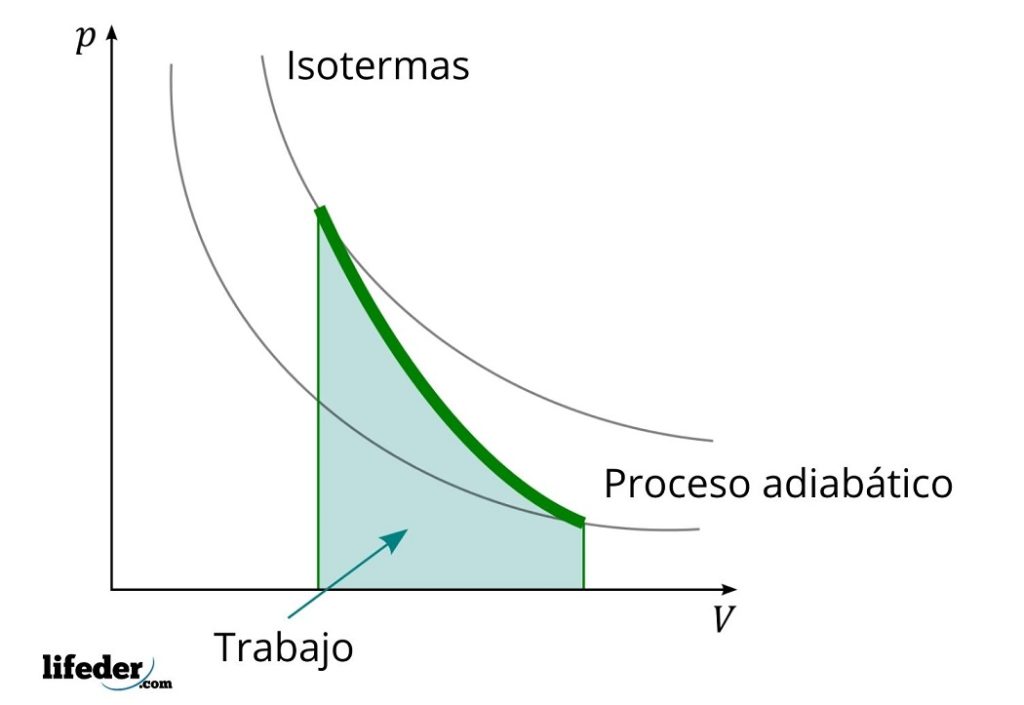
Otra característica importante de los procesos adiabáticos es que realizan o consumen trabajo proporcionalmente a la variación de la energía interna de sus sistemas; en este caso, de las de sus moléculas en fase gaseosa. Esto puede demostrarse gracias a la primera ley de la termodinámica.
En la vida diaria este tipo de proceso abarca sobre todo a los fenómenos geofísicos y, hasta cierto punto, el funcionamiento de los pistones en los motores Diesel. La transferencia de calor muchas veces se impide con el uso de un medio aislante, pero es la rapidez de estos procesos lo que permite su real desarrollo.
Índice del artículo
- 1 Procesos adiabáticos reversibles e irreversibles
- 2 Ejemplos de procesos adiabáticos
- 3 Ejercicios resueltos
- 4 Referencias
Los procesos adiabáticos pueden ser reversibles o irreversibles. Sin embargo, los primeros existen solo como herramientas teóricas para estudiar a los segundos. Es así pues, que los procesos adiabáticos reversibles involucran a los gases ideales, y carecen de fricción y cualquier otra eventualidad que ocasione una transferencia de calor entre el sistema y sus alrededores.
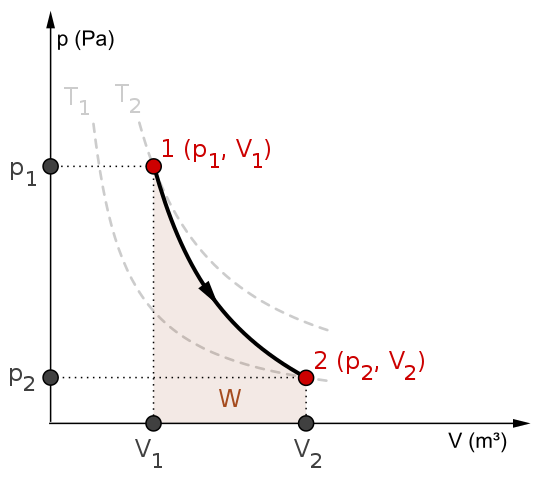
Considérese por ejemplo el diagrama P-V para el proceso adiabático reversible de arriba. T1 y T2 corresponden a dos isotermas, sobre las cuales las presiones P y los volúmenes V del sistema varían.
Entre los estados (P1, V1) y (P2, V2) se realiza una expansión adiabática reversible, ya que nos desplazamos de un volumen V1 a uno V2, más grande, siguiendo la dirección de la flecha.
Al hacerlo, el sistema se enfría, pero sin obedecer el comportamiento propio de las isotermas. El área bajo la curva corresponde al trabajo W, cuyo valor es positivo por tratarse de una expansión.
En este proceso la entropía permanece constante y, por lo tanto, se dice que es isoentrópico. El procesamiento matemático de esta reversibilidad genera un conjunto de ecuaciones con las cuales es posible evaluar otros sistemas.
Los procesos adiabáticos irreversibles, a diferencia de los reversibles, no se grafican en los diagramas P-V con líneas continuas sino punteadas, ya que solo los estados final e inicial tienen sus variables (P, V y T) bien definidas. Estos procesos involucran a los gases reales, por lo que la ecuación de los gases ideales y sus derivaciones no son directamente aplicables a ellos.
Transcurren rápidamente, impidiendo que haya transferencia de calor entre el sistema y sus alrededores. Asimismo, en ellos la entropía aumenta, tal como enuncia la segunda ley de la termodinámica.

Se mencionarán a continuación algunos ejemplos de procesos adiabáticos.
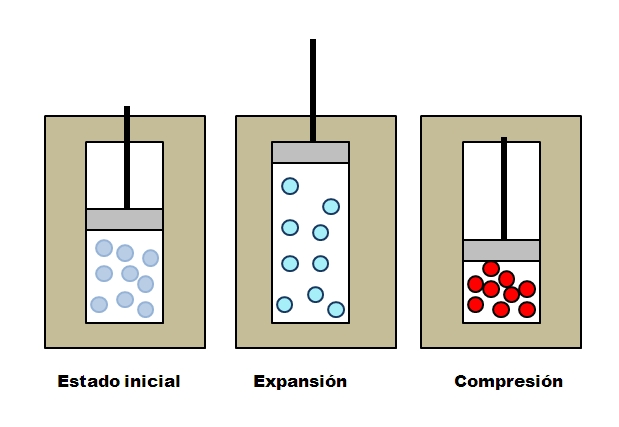
Supóngase tres chalecos aislantes que contienen compartimientos llenos con gas. En un estado inicial, el pistón no ejerce ninguna presión sobre el gas. Luego, se le permite al pistón elevarse, lo cual incrementa el volumen por donde puede desplazarse las moléculas del gas, ocasionando una disminución de su energía interna; y por consiguiente, un descenso de la temperatura.
Lo contrario sucede con la compresión adiabática: el pistón realiza trabajo sobre el gas, disminuyendo el volumen que puede ocupar sus moléculas. La energía interna esta vez aumenta, lo cual también implica un incremento de la temperatura, cuyo calor no puede dispersase hacia los alrededores a causa del chaleco aislante.
Los canales por donde asciende el magma dentro de un volcán cuentan como un medio aislante, el cual impide la transferencia de calor entre el magma y la atmósfera.
Los gases se perturban y expanden de acuerdo a la onda del sonido sin que enfríen o calienten el aire que las rodea.
El efecto Foehn es un ejemplo de los procesos adiabáticos en el campo de la geofísica. Las masas de aire ascienden hacia la parte alta de una montaña donde experimentan menos presión, por lo que sus moléculas se expanden y enfrían, dando lugar a la formación de la nube.
Sin embargo, apenas descienden por el otro lado de la montaña, la presión aumenta y, por ende, las moléculas se comprimen y elevan su temperatura, ocasionando que la nube desaparezca.
En el siguiente vídeo podrá apreciarse este fenómeno:
Para finalizar se resolverán un par de ejercicios. Es importante tener a la mano las siguientes ecuaciones:
ΔU = Q – W (Primera ley de la termodinámica)
Pero al no haber transferencia de calor, Q = 0 y:
ΔU = – W (1)
Esto es: si el trabajo W es positivo, ΔU es negativo, y viceversa. Por otro lado, tenemos también:
W = –nCVΔT (2)
Que tras aplicar la ecuación de los gases ideales (PV= nRT), y sustituyendo y resolviendo para T2 y T1 tendremos:
W = (CV/R)(P1V1 – P2V2) (3)
Siendo el valor de R igual a 0.082 L·atm/mol·K o 8.314 J/mol·K
En los procesos adiabáticos es importante conocer la relación CP/CV conocida como γ:
γ = CP/CV (4)
La cual permite establecer las relaciones T-V y P-V:
T1V1γ-1 = T2V2γ-1 (5)
P1V1γ = P2V2γ (6)
Y asimismo, los calores aproximados de CP y CV varían dependiendo de si los gases son monoatómicos, diatómicos, etc.
Un gas realiza 600 J de trabajo a través de un compartimiento aislado. ¿Cuál es el cambio de su energía interna? ¿Disminuye o aumenta la temperatura? Y considerando que se trate de un gas monoatómico, calcule además γ.
Datos:
W = +600J
ΔU= ¿?
γ= ¿?
El trabajo W es positivo porque el gas realiza trabajo sobre los alrededores. Al estar dentro de un compartimiento aislado, Q = 0, y por lo tanto tendremos la ecuación (1):
ΔU = – W
Es decir, ΔU es igual a:
ΔU = – (+600J)
= -600J
Lo cual quiere decir que la energía interna del gas disminuyó 600 J. Si ΔU disminuye, también lo hace la temperatura, por lo que el gas se enfría a consecuencia de haber realizado el trabajo.
Debido a que este gas es monoatómico,
CV = 3/2 R
CP = 5/2 R
Y siendo
γ = CP/CV
= (5/2 R) / (3/2 R)
= 5/3 o 1.66
En un contenedor 7 moles de O2 se comprimieron de un volumen de 15 litros a 9 litros. Sabiendo que la temperatura inicial era de 300 K, calcule: el trabajo realizado sobre el gas.
Datos:
n = 7 moles O2
T1 = 300 K
V1 = 15 L
V2 = 9 L
W = ¿?
Se trata de una comprensión adiabática irreversible. Tenemos dos ecuaciones para resolver W:
W = –nCVΔT (2)
W = (CV/R)(P1V1 – P2V2) (3)
Las presiones podemos calcularlas, pero para ahorrar tiempo es mejor proceder con la primera de las ecuaciones:
W = –nCVΔT
= –nCV (T2-T1)
Necesitamos CV y T2 para determinar W. El oxígeno, por ser un gas diatómico, posee un CV igual a 5/2 R:
CV (O2) = 5/2 R
= 5/2 (8.314 J/mol·K)
=20.785 J/mol·K
Falta calcular T2. Recurrimos a la ecuación (5):
T1V1γ-1 = T2V2γ-1
Pero antes de utilizarla hay que determinar primero CP y γ:
CP (O2) = 7/2 R
= 7/2 (8.314 J/mol·K)
=29.099 J/mol·K
Siendo γ igual a:
γ = CP/CV
= (29.099 J/mol·K) / 20.785 J/mol·K
= 1.4
Entonces, hecho esto podremos despejar T2 de la ecuación (5):
T1V1γ-1 = T2V2γ-1
T2 = (T1V1γ-1) / (V2γ-1)
= [(300K)(15L)1.4-1] / (9L)1.4-1
= 368.01 K
Y finalmente resolvemos para W:
W = –nCVΔT
= -(7 mol O2)( 20.785 J/mol·K)(368.01 K – 300 K)
=-9895.11 J o -9.895 kJ
Un contenedor de neón se expande adiabática e inicialmente a temperatura ambiente (T=298K) de 12 L a 14 L. Sabiendo que su presión inicial era de 3 atm, ¿cuál será el trabajo realizado por el gas?
Datos:
T1 = 298 K
V1 = 12 L
V2 = 14 L
P1 = 3 atm
W = ¿?
La ecuación (3) nos permite determinar W con los valores de las presiones:
W= (CV/R)(P1V1 – P2V2)
Pero nos faltan CV y P2.
La presión final podemos calcularla con la ecuación (6):
P1V1γ = P2V2γ
Siendo γ igual a CP/CV. Como el neón es un gas monoatómico, tenemos que sus valores de CP y CV son 5/2R y 3/2R, respectivamente. Calculamos entonces γ:
γ = CP/CV
= (5/2R) / (3/2R)
=5/3 o 1.66
Despejamos P2 de la ecuación (6):
P2 = (P1V1γ) / V2γ
= [(3 atm)(12 L)5/3] / (14 L)5/3
= 1.40 atm
Y el trabajo será igual a:
W= (CV/R)(P1V1 – P2V2)
= (3/2)[(3 atm)(12 L) – (1.40 atm)(14 L)] (101300 Pa/1 atm)(0.001 m3/L)(kJ/1000 J)
= 2.49 kJ
Se utilizan los factores de conversión para poder convertir el L·atm a Pa·m3, el cual equivale a 1 J. El gas neón se expande, por lo que su presión disminuye y, al realizar trabajo sobre los alrededores, este es positivo. Asimismo, su energía interna ΔU disminuye, al igual que su temperatura, enfriándose en el proceso de expansión.
- Walter J. Moore. (1963). Physical Chemistry. In Chemical kinetics. Fourth edition, Longmans.
- Ira N. Levine. (2009). Principios de fisicoquímica. Sexta edición. Mc Graw Hill.
- Wikipedia. (2020). Adiabatic process. Recuperado de: en.wikipedia.org
- Jones, Andrew Zimmerman. (18 de agosto de 2020). Thermodynamics: Adiabatic Process. Recuperado de: thoughtco.com
- DeVoe Howard & Neils Tom. (09 de agosto de 2020). Adiabatic changes. Chemistry LibreTexts. Recuperado de: chem.libretexts.org
