Definición de varianza
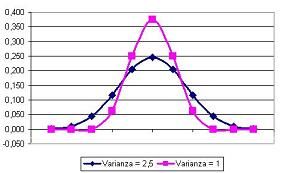 La noción de varianza se suele emplear en el ámbito de la estadística. Se trata de una palabra impulsada por el matemático y científico inglés Ronald Fisher (1890–1962) y sirve para identificar a la media de las desviaciones cuadráticas de una variable de carácter aleatorio, considerando el valor medio de ésta.
La noción de varianza se suele emplear en el ámbito de la estadística. Se trata de una palabra impulsada por el matemático y científico inglés Ronald Fisher (1890–1962) y sirve para identificar a la media de las desviaciones cuadráticas de una variable de carácter aleatorio, considerando el valor medio de ésta.
La varianza de las variables aleatorias, por lo tanto, consiste en una medida vinculada a su dispersión. Se trata de la esperanza del cuadrado de la desviación de esa variable considerada frente su media y se mide en una unidad diferente. Por ejemplo: en los casos en que la variable mide una distancia en kilómetros, su varianza se expresa en kilómetros al cuadrado.
Cabe destacar que las medidas de dispersión (también identificadas con el nombre de medidas de variabilidad) se encargan de expresar la variabilidad de una distribución por medio de un número, en los casos en que las diferentes puntuaciones de la variable están muy alejadas de la media. A mayor valor de la medida de dispersión, mayor variabilidad. En cambio, a menor valor, más homogeneidad.
Lo que hace la varianza es establecer la variabilidad de la variable aleatoria. Es importante tener en cuenta que, en ciertos casos, es preferible emplear otras medidas de dispersión ante las características de las distribuciones.
Se denomina varianza muestral cuando se calcula la varianza de una comunidad, grupo o población en base a una muestra. La covarianza, por otra parte, es la medida de dispersión conjunta de un par de variables.
Los expertos hablan de análisis de la varianza para nombrar a la colección de modelos estadísticos y sus procedimientos asociados en la cual la varianza aparece particionada en distintos componentes.
La desviación estándar o típica
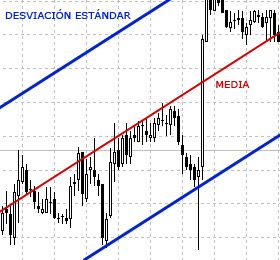 Uno de los conceptos más importantes relacionados con la varianza es la desviación estándar, también conocida como típica, que representa la magnitud de la dispersión de variables de intervalo y de razón, y resulta muy útil en el campo de la estadística descriptiva. Para obtenerla, simplemente se parte de la varianza y se calcula su raíz cuadrada.
Uno de los conceptos más importantes relacionados con la varianza es la desviación estándar, también conocida como típica, que representa la magnitud de la dispersión de variables de intervalo y de razón, y resulta muy útil en el campo de la estadística descriptiva. Para obtenerla, simplemente se parte de la varianza y se calcula su raíz cuadrada.
En la práctica, si tenemos los valores (expresados en milímetros) 14mm, 11mm, 10mm, 6mm y 4mm, podemos calcular su promedio sumándolos y dividiendo el resultado por 5, que es la cantidad de elementos. Obtendríamos 9mm. Para conocer la varianza, deberíamos restar cada uno de los valores a la media recién evidenciada, elevar cada resultado al cuadrado (para evitar números negativos que afecten el estudio), sumarlos entre sí y, finalmente, dividir todo por 5. La varianza es 93,8 milímetros cuadrados. Por último, para dar con la desviación estándar, calculamos la raíz cuadrada, lo que nos deja con 9.68mm (nótese que la unidad vuelve a ser milímetros).
Estos datos resultan muy útiles y necesarios para analizar y describir información, dado que nos ofrecen distintos puntos de vista, así como diferentes tendencias de los datos que caracterizan el objeto en cuestión y permiten establecer parámetros de comparación más complejos y dinámicos que los meros valores aislados o simplemente sometidos a su promedio aritmético.
En el procesos de comprobación de una teoría, es importante anticiparse a los posibles resultados, y la desviación sirve para analizar el comportamiento de los valores alrededor de su promedio. Establece nuevos puntos que abren puertas a diferentes clasificaciones y a datos que pueden no haber sido considerados en un principio.
Valiéndose tan sólo de la media entre un conjunto de valores, no es posible saber si alguno de ellos está excesivamente alejando de la «normalidad» existente en dicho contexto. La desviación estándar permite establecer dos nuevos límites alrededor de dicha línea central, para saber cuándo un elemento es demasiado pequeño o grande.
