Leyes de Kirchhoff: qué es, primera, segunda, ejemplos, ejercicios

¿Qué son las leyes de Kirchoff?

Las leyes de Kirchoff consisten en aplicar el principio de conservación de la carga eléctrica y el principio de conservación de la energía a los circuitos eléctricos, con la finalidad de resolver los que tienen varias mallas.

Estas reglas, ya que no son leyes en el sentido estricto, se deben al físico alemán Gustav Kirchoff (1824-1887). Su uso es imprescindible cuando la ley de Ohm no es suficiente para determinar voltajes y corrientes en el circuito.

Previo al enunciado y aplicación de las leyes de Kirchoff, es conveniente recordar el significado de algunos conceptos importantes sobre circuitos eléctricos:

• Nodo: punto de unión entre dos o más alambres conductores.
• Rama: elementos del circuito que se encuentran entre dos nodos consecutivos, a través de los cuales circula la misma corriente.
• Malla: trayectoria o lazo cerrado compuesto de dos o más ramas y que se recorre en un mismo sentido, sin pasar dos veces por el mismo punto.

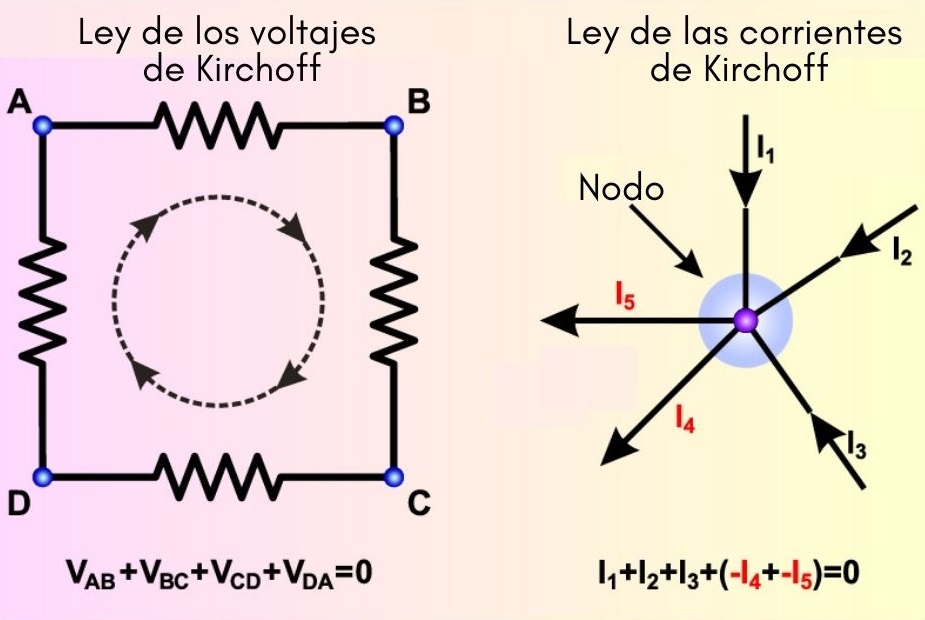
Primera ley de Kirchoff

Es conocida también como ley de las corrientes o regla de los nodos, y establece que:

La suma de las corrientes que entra a un nodo es igual a la suma de las corrientes que salen de él.

Así que, en forma matemática, la primera ley se expresa como:

∑ I = 0

Donde el símbolo Σ indica una sumatoria.

La ecuación anterior establece que, como la carga eléctrica no se crea ni se destruye, toda la corriente (carga por unidad de tiempo) que entra al nodo, debe ser igual a la que sale de él.

Ejemplo

Para aplicar convenientemente la ley de las corrientes, se le asigna un signo a las corrientes entrantes, y el signo opuesto a las corrientes salientes. La elección es completamente arbitraria.

En la siguiente imagen se muestran dos corrientes que entran a un nodo, dibujadas en rojo: I₁ e I₂, y que al salir se muestran en color verde: las corrientes I₃, I₄ e I₅.

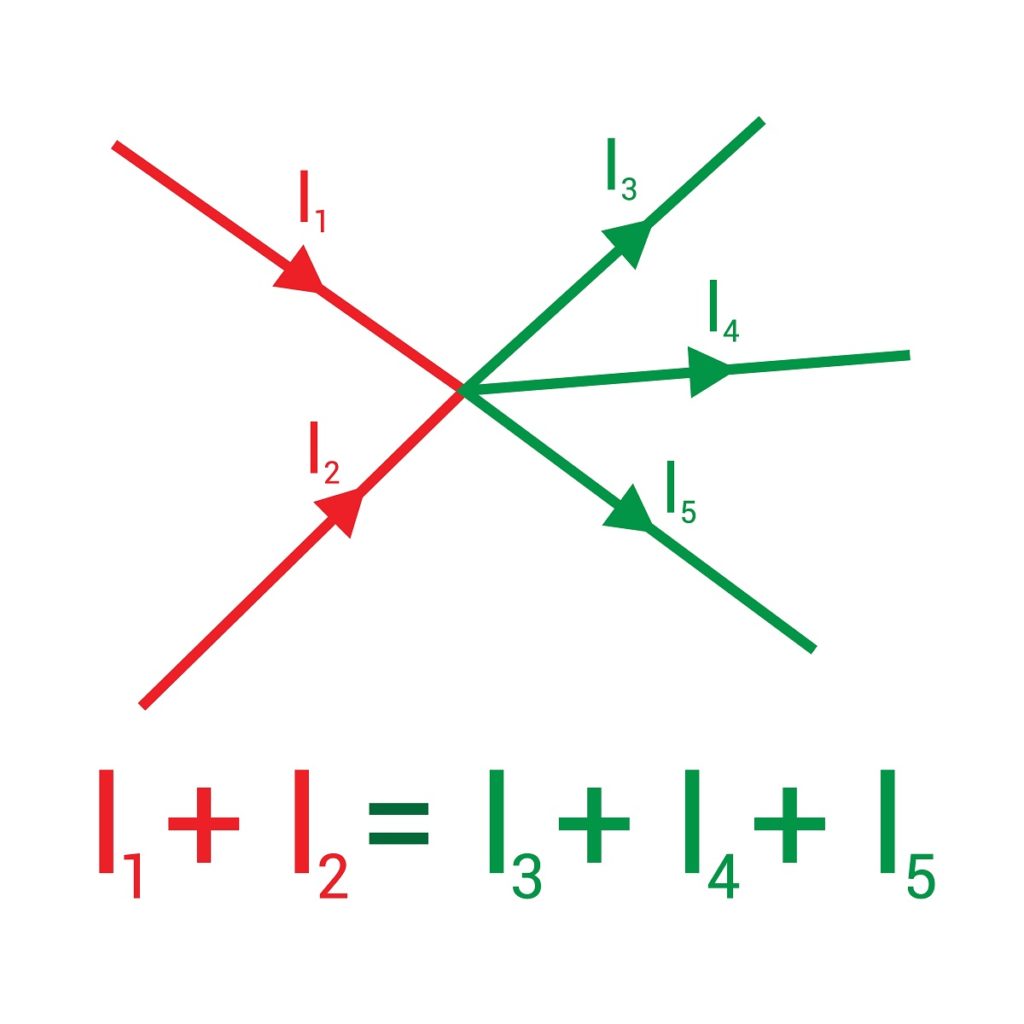
Asignando el signo (+) a las corrientes entrantes, y el (–) a las salientes, la primera regla de Kirchoff establece que:

I₁ + I₂ – I₃ – I₄ – I₅=0 ⇒ I₁ + I₂ = I₃ + I₄ + I₅

Segunda ley de Kirchoff

Otros nombres para la segunda ley de Kirchoff son: ley de los voltajes, ley de las tensiones o ley de las mallas. En cualquier caso, establece que:

La suma algebraica de las caídas de tensión a lo largo de una malla es igual a 0.

Esta es una forma de aplicar la conservación de la energía en el circuito, ya que el voltaje en cada elemento es el cambio de energía por unidad de carga.

Por lo tanto, al recorrer una porción cerrada (una malla), la suma algebraica de las subidas y caídas de tensión es 0 y se puede escribir:

∑ V = 0

Ejemplo

En la siguiente figura se tiene la malla abcda, por la cual circula una corriente I en el sentido de las agujas del reloj y el recorrido se puede empezar en cualquier punto del circuito.

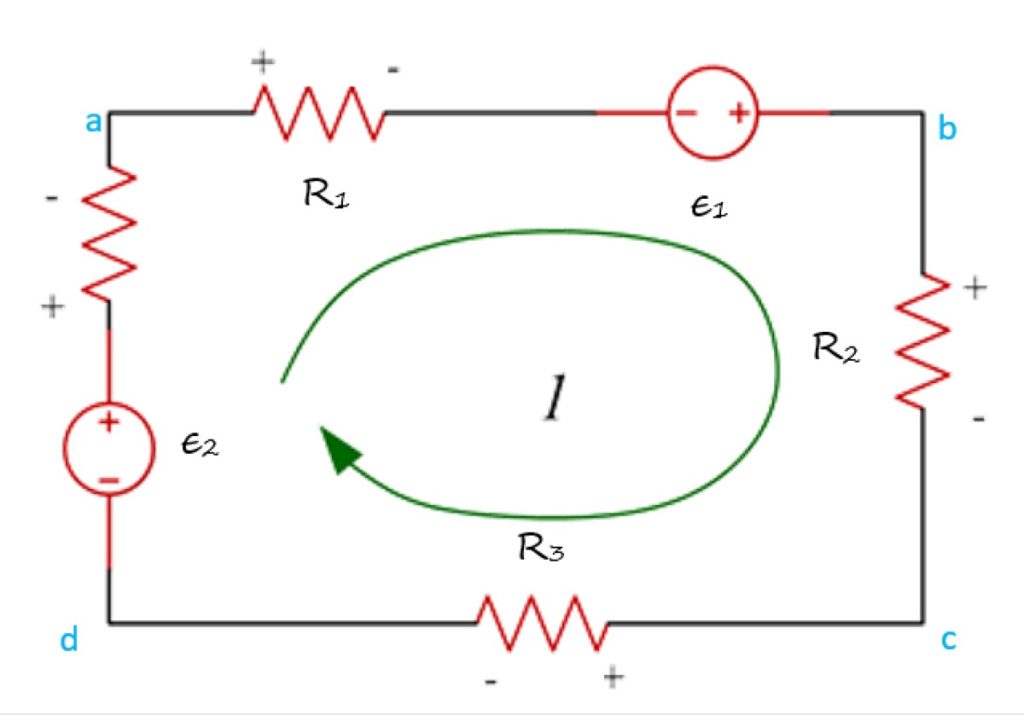
También es necesario establecer una convención de signos al aplicar la regla de los voltajes de Kirchoff, al igual que se hizo con la regla de las corrientes. Lo usual es asignar como positiva la subida de tensión, es decir, cuando la corriente circula desde (−) a (+). Entonces, la caída de tensión, que ocurre cuando la corriente va de (+) a (−), es negativa.

Iniciando el recorrido de la malla en el punto “a”, se encuentra la resistencia R₁. En ella, las cargas experimentan una caída de potencial, simbolizada mediante los signos (+) a la izquierda y (−) arriba de la resistencia.

Por lo tanto, el voltaje o tensión en R₁ tiene signo negativo.

Seguidamente se llega a una fuente de voltaje directo, llamada ε₁, cuya polaridad es de menos (−) a más (+). Allí las cargas eléctricas pasan por una subida de potencial y a esta fuente se la considera como positiva.

Siguiendo este procedimiento para las restantes resistencias y la otra fuente, se obtiene como resultado la siguiente ecuación:

−V₁ + ε₁ – V₂ – V₃ + ε₂ = 0

Donde V₁, V₂ y V₃ son las tensiones en las resistencias R₁, R₂ y R₃. Dichas tensiones se pueden encontrar a partir de la ley de Ohm: V = I·R.

Ejercicio resuelto

Encontrar el valor de las corrientes I₁, I₂ e I₃ mostradas en la figura.

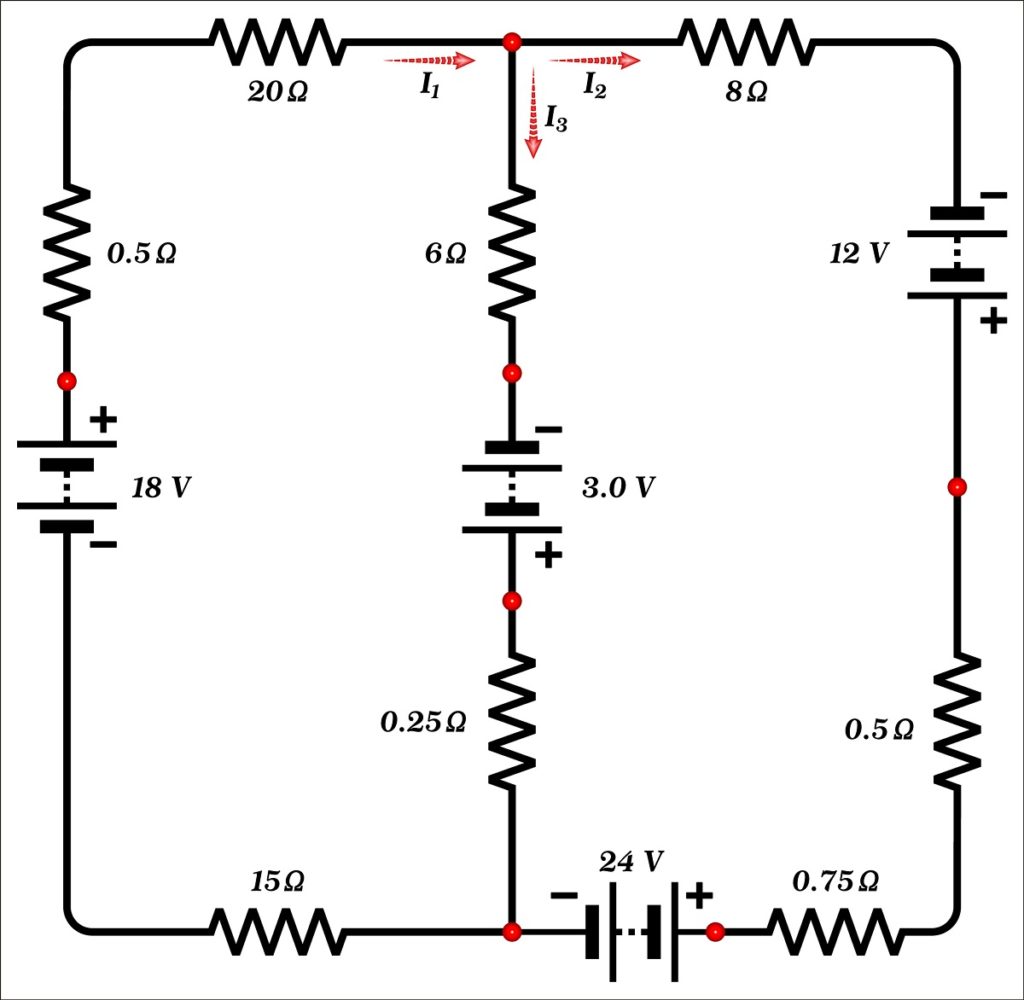
Solución

Este circuito consta solamente de dos mallas y tiene 3 incógnitas: las corrientes I₁, I₂ e I₃, por lo que se requieren al menos 3 ecuaciones para hallar la solución.

En el nodo (punto marcado en rojo) que está en la parte superior del circuito sobre la rama central, se observa que la corriente I₁ es entrante, mientras que las corrientes I₂ e I₃ son salientes.

Por lo tanto, la ley de las corrientes de Kirchoff conduce a la primera ecuación:

1) I₁ − I₂ − I₃ = 0

El nodo inferior da la misma información, por lo tanto, el siguiente paso es recorrer las mallas.

Primera malla

Para establecer la siguiente ecuación, la malla de la izquierda se recorre en sentido horario, partiendo de la esquina superior izquierda. Este es el sentido en el que circulan las corrientes I₁ e I₃.

Nótese que:

• I₁ pasa a través de las resistencias de 20 Ω, 15 Ω y 0.5 Ω y la batería de 18 V, donde experimenta una subida de potencial.
• Por su parte, I₃ atraviesa las resistencias de la rama central de 6 Ω y 0.15 Ω y en la batería de 3.0 V se encuentra una subida de potencial.

Asimismo, se utiliza la ley de Ohm V= I∙R para establecer la tensión en cada resistencia, de acuerdo a esto:

−20∙I₁ − 6∙I₃ + 3.0 − 0.25∙I₃ −15∙I₁ + 18.0 − 0.5∙I₁ = 0

Ordenando los términos:

(−20 −15 − 0.5) ∙I₁ – (6 + 0.25)∙I₃  = − 3.0 – 18.0

−35.5∙I₁ – 6.25∙I₃ = – 21.0

2) 5∙I₁ + 6.25∙I₃ = 21.0

Segunda malla

La tercera ecuación se obtiene recorriendo la malla de la derecha, comenzando en el nodo de la parte superior del circuito. Se observa que:

• I₂ pasa por las resistencias de 8 Ω, 0.5 Ω y 0.75 Ω, más las baterías de 12 V y 24 V. Según la polaridad de las baterías, en el recorrido hay subida de potencial en la de 12 V y disminución en la de 24 V.
• Importante: el recorrido de la segunda malla (en sentido horario) es opuesto a I₃, por lo tanto, los voltajes en las resistencias de 6 Ω y 0.25 Ω son subidas de potencial y llevan signo positivo. De acuerdo a la polaridad de las baterías, hay subida en la de 12 V y caída en las de 24 V y 3 V.

Con todo esto se llega a:

−8∙I₂ − 0.5∙I₂ − 0.75∙I₂ + 12.0 − 24.0 + 0.25∙I₃ − 3.0 + 6∙I₃ = 0

3) −25∙I₂ + 6.25∙I₃ = 15.0

Cálculo de las corrientes

Las ecuaciones 1), 2) y 3) forman un sistema de 3 ecuaciones lineales con 3 incógnitas, cuya solución es:

I₁ = 0.381 A; I₂ = -0.814 A; I₃ = 1.195 A

El signo negativo en la corriente I₂ significa que fluye en sentido opuesto al del esquema.