Ley de Hess: explicación, aplicaciones, ejemplos

La ley de Hess es otra manifestación de la ley de conservación de la energía que permite determinar, mediante simples sumas algebraicas, la entalpía de una reacción química. Entiéndase por entalpía como el calor liberado o absorbido, a presión constante, que viene asociado a toda reacción química o fenómeno químico.

Las entalpías, ΔH, se determinan experimentalmente haciendo uso de la calorimetría. Sin embargo, hay reacciones que resultan difíciles de estudiar con esta técnica. Cuando esto sucede, se recurre a otras reacciones que sí tengan sus entalpías determinadas, y que posean los elementos o compuestos que interesan.

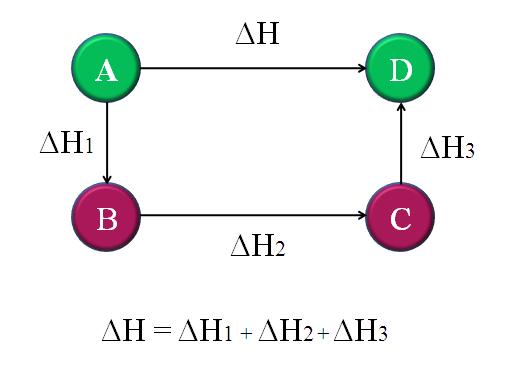
De esta manera, se puede calcular el ΔH “desconocido” de la reacción. Por ejemplo, el diagrama de arriba ayuda a comprender esta idea. Hay cuatro reacciones: A-D, A-B, B-C y C-D. La reacción A-D es la que tiene el mayor ΔH, pues en la que se producen, por decirlo así, los cambios químicos más notorios.

Las demás reacciones, mientras, tienen ΔH más pequeños, ya que consisten de pasos alternativos o reacciones alternas para llegar a los mismos productos D. Por lo tanto, la sumatoria de ΔH₁, ΔH₂ y ΔH₃, será igual a ΔH. Sabiendo esto, ΔH, o cualquier otra entalpía, podrá calcularse aplicando simples despejes. Esto es la ley de Hess.

La ley de Hess es muy útil al momento de calcular entalpías reacción, así como las entalpías de formación para distintos compuestos o intermediarios inestables.

Índice del artículo

• 1 Explicación de la ley de Hess
  • 1.1 Cálculo de la entalpía de una reacción
  • 1.2 Entalpía de una reacción a partir de entalpías de formaciones
  • 1.3 Sumas de reacciones
• 2 Aplicaciones de la ley de Hess
• 3 Ejemplos: ejercicios resueltos
  • 3.1 – Ejemplo 1
  • 3.2 – Ejemplo 2
• 4 Referencias

Explicación de la ley de Hess

Cálculo de la entalpía de una reacción

La razón por la que se cumple que:

ΔH = ΔH₁ + ΔH₂ + ΔH₃

Es porque la entalpía, o el cambio de entalpía, es una función de estado. Esto quiere decir que sus valores no se ven modificados por el número de pasos, etapas o reacciones intermediarias. Por ejemplo, ΔH seguirá siendo el mismo aun cuando haya un ΔH₁₀ que deba considerarse en la suma algebraica.

Las entalpías pudieran visualizarse como las cimas de unas montañas. No importa cómo se encaminan los pasos hacia ellas, la altura que las separa del nivel del mar jamás variará. Y precisamente son las alturas las que se suman o restan para determinar la altura desconocida de una montaña aledaña.

Volviendo al diagrama anterior: A, es una montaña, D otra montaña, y así sucesivamente. La diferencia de altura entre las cimas de A y D, es la mayor. Sumando las alturas entre A-B, B-C y C-D, dará igual a la altura A-D. Esto es lo que se hace con las entalpías de sus respectivas reacciones químicas.

Entalpía de una reacción a partir de entalpías de formaciones

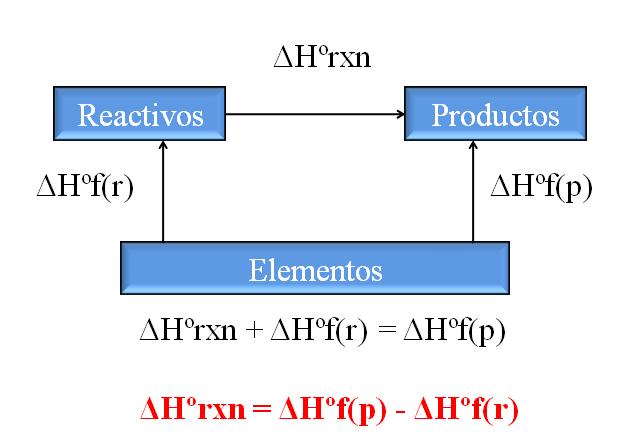
Una de las consecuencias más valiosas de la ley de Hess es que permite la determinación de las entalpías de cualquier reacción química, tomando las entalpías de formación de todos los compuestos (reactivos y productos) involucrados.

La imagen superior ilustra este punto. Entiéndase por entalpía de formación al calor asociado cuando un compuesto se forma a partir de sus elementos. Dicha entalpía vendría a ser la máxima diferencia posible entre reactivos y productos, sin necesidad de consultar otras reacciones químicas; al menos, ajenas a la formación por separado de los compuestos.

¿Cómo se lee el diagrama esta vez? Un truco es siempre sumar las entalpías cuando se vaya en dirección de la flecha, y restarlas cuando la fleche esté en vía contraria. Así, ΔHºrxn, entalpía de reacción estándar, se suma a ΔHºf(reactivos), entalpía estándar de formación de los reactivos, y se les resta ΔHºf(productos), entalpía estándar de formación de los productos.

Sumas de reacciones

Los diagramas pueden tornarse muy complicados de interpretar, sobre todo cuando hay muchas reacciones que deben considerarse. Por eso, se recurre a la suma de las reacciones. Este método facilita enormemente el cálculo de las entalpías, y agiliza la comprensión de la ley de Hess.

Supóngase por ejemplo que se desea determinar el ΔHºrxn de la siguiente reacción:

A + B + C → ABC

Y tenemos además otras dos reacciones:

A + B → AB  (ΔHº₁)

AB + C → ABC (ΔHº₂)

Interesa que A + B + C estén del lado izquierdo (reactivos) y que ABC esté en el lado derecho (productos). Entonces, se procede sencillamente a sumar las últimas dos reacciones:

A + B → AB

AB + C → ABC

A + AB + C → ABC + AB

Como AB está de ambos lados se elimina. Y así tenemos:

A + B + C → ABC

ΔHºrxn = ΔHº₁ + ΔHº₂

Sumando las reacciones, se omite el uso de todo diagrama.

Aplicaciones de la ley de Hess

La ley de Hess permite obtener, sin necesidad de experimentos, las entalpías para distintas reacciones o fenómenos químicos. Algunas de ellas se enlistan abajo:

– Entalpías de formación para compuestos o intermediarios inestables, como suele haberlos en química orgánica.

-Entalpías de transiciones de fase, en el estudio de sólidos cristalinos.

-Entalpías de transiciones alotrópicas, como la que ocurre entre el grafito y el diamante.

Asimismo, la ley de Hess se utiliza para determinar la energía reticular de un sólido, y las afinidades electrónicas de algunos átomos.

Ejemplos: ejercicios resueltos

– Ejemplo 1

Calcule el ΔHrxn de la siguiente reacción:

2HCl(g) + F₂(g) → 2HF(l) + Cl₂(g)

Si se tiene a la mano las siguientes reacciones y sus respectivas entalpías:

4HCl(g) + O₂(g) → 2H₂O(l) + 2Cl₂(g)  (ΔH = -202.4 kJ/mol)

1/2H₂(g) + 1/2F₂(g) → HF(l)  (ΔH = -600.0 kJ/mol)

H₂(g) + 1/2O₂(g) → H₂O(l)  (ΔH = -285.8 kJ/mol)

Ordenamiento de las ecuaciones

Para empezar, debemos sumar las reacciones de tal modo que HCl y F₂ estén en el lado izquierdo, y HF y Cl₂, en el lado derecho. Pero más importante, es notar que tanto H₂ como H₂O no están en la ecuación de interés. Por lo tanto, debemos cancelarlos en la suma, y hacer que coincidan los coeficientes estequiométricos mediante multiplicaciones:

2HCl(g) + 1/2O₂(g) → H₂O(l) + Cl₂(g)  (ΔH = -202.4 kJ/mol) * (1/2)

Se multiplicó esta ecuación por 1/2 para tener 2HCl en lugar de 4HCl

H₂(g) + F₂(g) → 2HF(l)  (ΔH = -600.0 kJ/mol) * (2)

Esta ecuación se multiplicó por 2 para tener F₂ y no 1/2F₂

H₂O(l)  → H₂(g) + 1/2O₂(g) (ΔH = -285.8 kJ/mol) * (-1)

Mientras, esta última se multiplicó por -1 para poder “voltearla”. Así, tenemos las ecuaciones ordenadas y listas para sumar.

Suma de las ecuaciones

Sumando todo nos da:

2HCl(g) + 1/2O₂(g) → H₂O(l) + Cl₂(g)  (ΔH = -101.2 kJ/mol)

H₂(g) + F₂(g) → 2HF(l)  ΔH = -1200.0 kJ/mol)

H₂O(l)  → H₂(g) + 1/2O₂(g) (ΔH = 285.8 kJ/mol)

2HCl(g) + F₂(g)  →  2HF(l)  +  Cl₂(g)

Nótese que los términos 1/2O₂, H₂O y H₂ se cancelan porque están en ambos lados de la flecha. Las entalpías también se suman, dando:

ΔHrx = 285.8 kJ/mol + (-101.2 kJ/mol) + (-1200.0 kJ/mol)

Esta expresión es la misma que la del principio:

ΔH = ΔH₁ + ΔH₂ + ΔH₃

Y así, tenemos que ΔHrx es igual a:

ΔHrx = -1015.4 kJ/mol

– Ejemplo 2

En este ejemplo se verá que las entalpías de las reacciones alternas corresponden a las propias entalpías de formación de los compuestos de interés.

Se desea determinar ΔHrxn para la siguiente reacción de descomposición:

2SO₃(g) → 2SO₂(g) + O₂(g)

Y se cuenta a la mano con las entalpías de formación de los compuestos SO₃ y SO₂:

S(s) + O₂(g) → SO₂(g)  (ΔH = -296.8 kJ/mol)

S(s) + 3/2O₂(g) → SO₃(g)  (ΔH = -395.6 kJ/mol)

Ordenamiento de las ecuaciones

Se procederá a resolver este ejercicio del mismo modo que el ejemplo anterior. Conviene que SO₃ esté a la derecha, y que se multiplique por 2. Para eso, debemos “voltear” la ecuación de formación de SO₃ multiplicándola por -1, y luego por multiplicándola por 2:

2SO₃(g)  → 2S(s) + 3O₂(g) (ΔH = -395.6 kJ/mol) * (-2)

La ecuación de formación de SO₂ también la multiplicamos por 2:

2S(s) + 2O₂(g) → 2SO₂(g)  (ΔH = -296.8 kJ/mol) * (2)

Suma de las ecuaciones

Ahora se procede a sumar las ecuaciones:

2SO₃(g)  → 2S(s) + 3O₂(g) (ΔH = 791.2 kJ/mol)

2S(s) + 2O₂(g) → 2SO₂(g)  (ΔH = -593.6 kJ/mol)

2SO₃(g)  → 2SO₂(g)  + O₂(g)

Nótese que se elimina el término 2S porque está en ambos lados de la flecha. Asimismo, a 3O₂ se le resta 2O₂ dando un O₂. La suma de las entalpías, y por tanto, el valor de ΔHrxn será:

ΔH = ΔHrxn = 791.2 kJ/mol + (-593.6 kJ/mol)

= 197.6 kJ/mol

Como toda reacción de descomposición, es endotérmica, por lo que su entalpía es positiva.

Método alternativo

Hay un método para llegar a este mismo resultado de manera más directa y sencilla. Este se mencionó en un apartado anterior.

2SO₃(g) → 2SO₂(g) + O₂(g)

Para determinar el ΔHrxn de esta reacción, debemos calcular ΔHºf(reactivos) y ΔHºf(productos). El ΔHºf(SO₃) es igual a -395.6 kJ/mol, mientras que el ΔHºf(SO₂) es igual a -296.8 kJ/mol. El ΔHºf(O₂) es igual a 0, ya que el oxígeno elemental existe como una molécula de O₂ y no como átomos O libres.

Entonces tenemos:

ΔHrxn = ΔHºf(productos) – ΔHºf(reactivos)

= [ΔHºf(SO₂) + ΔHºf(O₂)] – ΔHºf(SO₃)

= ΔHºf(SO₂) – ΔHºf(SO₃)

Sin embargo, debemos multiplicar ambas entalpías de formación por 2, para así igualar los coeficientes estequiométricos con respecto a la ecuación química:

ΔHrxn = 2ΔHºf(SO₂) – 2ΔHºf(SO₃)

Y calculando tenemos:

ΔHrxn = 2(-296.8 kJ/mol) – 2(-395.6 kJ/mol)

= 197.6 kJ/mol

De hecho, este es el modo como usualmente se prefiere resolver todos los ejercicios en los que se aplica la ley de Hess.

Referencias

1. Whitten, Davis, Peck & Stanley. (2008). Química. (8va ed.). CENGAGE Learning.
2. Wikipedia. (2020). Hess’s law. Recuperado de: en.wikipedia.org
3. Cohen Shelly. (18 de mayo de 2020). Hess’s law. Chemistry LibreTexts. Recuperado de: chem.libretexts.org
4. Clark Jim. (2010). Hess’s law and Enthalpy Change Calculations. Recuperado de: chemguide.co.uk
5. Helmenstine, Anne Marie, Ph.D. (11 de febrero de 2020). Hess’s Law Definition. Recuperado de: thoughtco.com
6. Foist Laura. (2020). Hess’s Law: Definition, Formula & Examples. Study. Recuperado de: study.com
7. QuimiTube. (2014). Teoría 14 Termoquímica: Cálculo de la entalpía de una reacción por la Ley de Hess. Recuperado de: quimitube.com