Choques elásticos: en una dimensión, casos especiales, ejercicios

Los choques elásticos o colisiones elásticas consisten en interacciones breves pero intensas entre objetos, en las cuales tanto la cantidad de movimiento como la energía cinética se conservan. Los choques son sucesos muy frecuentes en la naturaleza: desde partículas subatómicas hasta galaxias, pasando por bolas de billar y autos de choque en los parques de atracciones, todos son objetos capaces de colisionar.

Durante una colisión o choque, las fuerzas de interacción entre los objetos son muy intensas, mucho más que las que puedan actuar externamente. De esta forma se puede afirmar que durante la colisión, las partículas forman un sistema aislado.

En tal caso se cumple que:

P_o = P_f

La cantidad de movimiento P_o antes de la colisión es la misma que después de la colisión. Esto se cumple para cualquier tipo colisión, tanto elástica como inelástica.

Ahora hay que considerar lo siguiente: durante una colisión los objetos experimentan una cierta deformación. Cuando el choque es elástico, los objetos recobran rápidamente su forma original.

Índice del artículo

• 1 Conservación de la energía cinética
• 2 Choques elásticos en una dimensión
  • 2.1 -Fórmulas para las colisiones elásticas
• 3 Casos especiales en las colisiones elásticas
  • 3.1 Dos masas idénticas
  • 3.2 Dos masas idénticas, una de las cuales estaba inicialmente en reposo
  • 3.3 Dos masas diferentes, una de ellas inicialmente en reposo
• 4 Coeficiente de restitución o regla de Huygens-Newton
• 5 Ejercicios resueltos
  • 5.1 -Ejercicio resuelto 1
  • 5.2 -Ejercicio resuelto 2
  • 5.3 -Ejercicio resuelto 3
  • 5.4 -Ejercicio resuelto 4
• 6 Referencias

Conservación de la energía cinética

Normalmente durante un choque parte de la energía de los objetos se gasta en calor, deformación, sonido y en ocasiones hasta en producir luz. Así que la energía cinética del sistema después de la colisión es menor que la energía cinética original.

Cuando la energía cinética K, se conserva entonces:

K_o = K_f

Lo cual significa que las fuerzas que actúan durante la colisión son conservativas. Mientras dura la colisión la energía cinética se transforma brevemente en energía potencial y luego vuelve a ser energía cinética. Las energías cinéticas respectivas varían, pero la suma se mantiene constante.

Las colisiones perfectamente elásticas no son frecuentes, aunque las bolas de billar son una aproximación bastante buena, así como las colisiones que tienen lugar entre las moléculas de los gases ideales.

Choques elásticos en una dimensión

Examinemos una colisión de dos partículas de este en una sola dimensión; es decir, las partículas que interactúan se mueven, digamos, a lo largo del eje x. Supongamos que tienen masas m₁ y m₂. Las velocidades iniciales de cada una son u₁ y u₂ respectivamente. Las velocidades finales son v₁ y v₂.

Podemos prescindir de la notación vectorial, ya que el movimiento se realiza a lo largo del eje x, sin embargo, los signos (-) y (+) indican el sentido del movimiento. A la izquierda es negativo y a la derecha positivo, por convención.

-Fórmulas para las colisiones elásticas

Para la cantidad de movimiento

m₁u₁ + m₂u₂ =m₁v₁ + m₂v₂

Para la energía cinética

½ m₁u²₁ + ½ m₂u²₂ =½ m₁v²₁ +  ½ m₂v²₂

Siempre que se conozcan las masas y las velocidades iniciales, es posible reagrupar las ecuaciones para encontrar las velocidades finales.

El problema es que en principio, es necesario llevar a cabo un poco de álgebra bastante tediosa, pues las ecuaciones para la energía cinética contienen los cuadrados de las velocidades, lo cual hace un poco engorroso el cálculo. Lo ideal sería encontrar expresiones que no los contengan.

Lo primero es prescindir del factor ½ y reordenar ambas ecuaciones de tal forma que aparezca un signo negativo y las masas se puedan factorizar:

m₁u₁ – m₁v₁ =  m₂v₂ – m₂u₂

m₁u²₁ – m₁v²₁  = +   m₂v²₂ – m₂u²₂

Quedando expresadas de esta manera:

m₁(u₁ – v₁ ) = m₂(v₂ – u₂)

m₁(u²₁ – v²₁ )= m₂ (v²₂ – u²₂)

Simplificación para eliminar los cuadrados de las velocidades

Ahora hay que hacer uso del producto notable suma por su diferencia en la segunda ecuación, con lo cual se obtiene una expresión que no contiene los cuadrados, tal como se quería originalmente:

m₁(u₁ – v₁ ) = m₂(v₂ – u₂)

m₁(u₁ – v₁ ) (u₁ + v₁ )= m₂ (v₂ – u₂) (v₂ + u₂)

El siguiente paso es sustituir la primera ecuación en la segunda:

m₂(v₂ – u₂) (u₁ + v₁ )= m₂ (v₂ – u₂) (v₂ + u₂)

Y al estar repetido el término m₂(v₂ – u₂) a ambos lados de la igualdad dicho término se cancela y queda así:

(u₁ + v₁)= (v₂ + u₂)

O aún mejor:

u₁ – u₂= v₂ –  v₁

Velocidades finales v₁ y v₂ de las partículas

Ahora se dispone de dos ecuaciones lineales con las que es más fácil trabajar. Las volveremos a colocar una debajo de la otra:

m₁u₁ + m₂u₂ =m₁v₁ + m₂v₂

u₁ – u₂= v₂ –  v₁

Multiplicando la segunda ecuación por m₁ y sumando término a término queda:

m₁u₁ + m₂u₂ =m₁v₁ + m₂v₂

m₁u₁ – m₁u₂= m₁v₂ – m₁ v₁

—————————————–

2 m₁u₁ + ( m₂ – m₁) u₂ = (m₂ + m₁) v₂

Y ya es posible despejar v₂. Por ejemplo:

Casos especiales en las colisiones elásticas

Ahora que se dispone de ecuaciones para las velocidades finales de ambas partículas, es hora de analizar algunas situaciones especiales.

Dos masas idénticas

En ese caso m₁ = m₂ = m y:

v₁ = u₂

v₂ = u₁

Las partículas simplemente intercambian sus velocidades después de la colisión.

Dos masas idénticas, una de las cuales estaba inicialmente en reposo

De nuevo  m₁ = m₂ = m y suponiendo que u₁ = 0:

v₁ = u₂

v₂ = 0

Después del choque la partícula que estaba en reposo adquiere la misma velocidad de la partícula que se venía moviendo, y esta a su vez se detiene.

Dos masas diferentes, una de ellas inicialmente en reposo

En este caso supongamos que u₁ = 0, pero las masas son distintas:

¿Qué pasa si m₁ es mucho mayor que m₂?

Sucede que m₁ sigue en reposo y m₂ se devuelve con la misma rapidez con la que impactó.

Coeficiente de restitución o regla de Huygens-Newton

Anteriormente se dedujo la siguiente relación entre las velocidades para dos objetos en colisión elástica: u₁ – u₂ = v₂ –  v₁. Estas diferencias son las velocidades relativas antes y después de la colisión. En general, para una colisión se cumple que:

u₁ – u₂ = -(v₁ –  v₂)

El concepto de velocidad relativa se aprecia mejor si el lector imagina que está sobre una de las partículas y desde esta posición observa la velocidad con que la otra partícula se mueve. La ecuación anterior se reescribe así:

Ejercicios resueltos

-Ejercicio resuelto 1

Una bola de billar se mueve hacia la izquierda a 30 cm/s, colisionando  de frente con otra bola idéntica que se mueve hacia la derecha a 20 cm/s. Las dos bolas tienen la misma masa y el choque es perfectamente elástico. Encontrar la velocidad de cada bola después del impacto.

Solución

u₁ = -30 cm/s

u₂ = +20 cm/s

Se trata del caso especial en que dos masas idénticas colisionan en una dimensión elásticamente, por lo tanto las velocidades se intercambian.

v₁ = +20 cm/s

v₂ = -30 cm/s

-Ejercicio resuelto 2

El coeficiente de restitución de una pelota que rebota en el suelo es igual a 0,82. Si cae desde el reposo, ¿qué fracción de su altura original alcanzará la pelota después de rebotar una vez? ¿Y después de 3 rebotes?

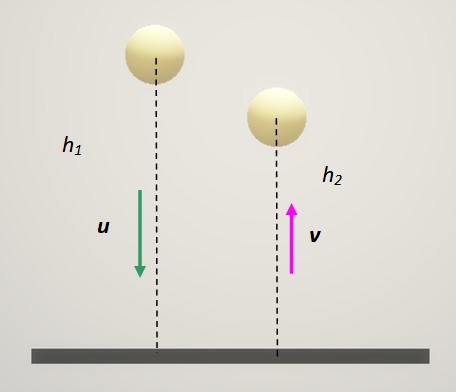
Solución

El suelo puede ser el objeto 1 en la ecuación del coeficiente de restitución. Y siempre queda en reposo, de manera que:

Con esta velocidad rebota:

El signo + indica que se trata de una velocidad ascendente. Y de acuerdo a ella, la pelota alcanza una altura máxima de:

Ahora regresa al suelo de nuevo con velocidad de igual magnitud, pero signo contrario:

Con ello alcanza una altura máxima de:

Llega de nuevo al suelo con:  

Rebotes sucesivos

Cada vez que la pelota rebota y asciende hay que multiplicar la velocidad de nuevo por 0.82:

A estas alturas h₃ es aproximadamente el 30% de h_o. ¿Cuál sería la altura al 6to rebote sin necesidad de hacer cálculos tan detallados como los anteriores?

Sería h₆ = 0.82¹² h_o = 0.092h_o o apenas el 9% de h_o.

-Ejercicio resuelto 3

Un bloque de 300 g se mueve hacia el norte a 50 cm/s y choca contra un bloque de 200 g que se dirige hacia el sur a 100 cm/s. Suponga que el choque es perfectamente elástico. Encuentre las velocidades después del impacto.

Datos

m₁ = 300 g ; u₁ = + 50 cm/s

m₂ = 200 g ; u₂ = -100 cm/s

-Ejercicio resuelto 4

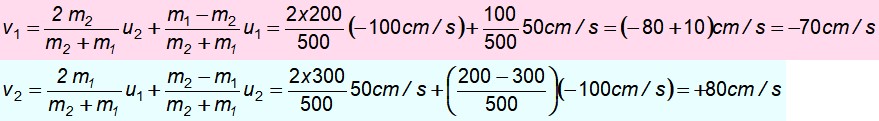
Se libera una masa de m₁ = 4 kg desde el punto indicado sobre la pista sin fricción, hasta que colisiona con m₂ = 10 kg en reposo. ¿Hasta que altura se eleva m₁ después de la colisión?

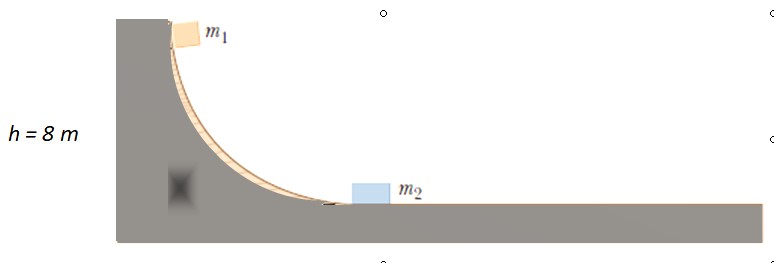
Solución

Puesto que no hay rozamiento, se conserva la energía mecánica para encontrar la velocidad u₁ con que m₁ impacta a  m_2. Inicialmente la energía cinética es 0, puesto que m₁ parte del reposo. Cuando se mueve sobre la superficie horizontal no tiene altura, por lo cual la energía potencial es 0.

mgh = ½ mu₁²

u₂ = 0

Ahora se calcula la velocidad de m₁ después de la colisión:

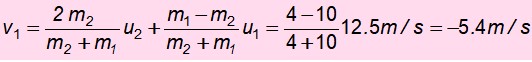
El signo negativo significa que se ha devuelto. Con esta velocidad asciende y se conserva la energía mecánica de nuevo para encontrar h’, la altura a la cual logra ascender después del choque:

½ mv₁² =mgh’

Obsérvese que no regresa al punto de partida a 8 m altura. No tiene energía suficiente porque cedió parte de su energía cinética la masa m_1.

Referencias

1. Giancoli, D.  2006. Physics: Principles with Applications. 6^th. Ed Prentice Hall. 175-181
2. Rex, A. 2011. Fundamentos de Física. Pearson. 135-155.
3. Serway, R., Vulle, C. 2011. Fundamentos de Física. 9^na Cengage Learning. 172 -182
4. Tipler, P. (2006) Física para la Ciencia y la Tecnología. 5ta Ed. Volumen 1. Editorial Reverté. 217-238
5. Tippens, P. 2011. Física: Conceptos y Aplicaciones. 7ma Edición. MacGraw Hill. 185 -195