Suma de vectores: método gráfico, ejemplos, ejercicios resueltos
La suma de vectores es la operación de adición entre vectores que da como resultado otro vector. Los vectores se caracterizan por tener magnitud, y además dirección y sentido. Por lo tanto no es posible, en general, sumarlos como se haría con cantidades escalares, es decir, adicionando números.
Al vector que se obtiene de la suma de varios vectores se le llama vector resultante. En Mecánica se habla de la fuerza resultante, que es la suma vectorial de todas las fuerzas sobre un cuerpo. Dicha resultante es equivalente al conjunto o sistema de fuerzas.

Para especificar completamente el vector suma es preciso indicar la magnitud y la unidad, la dirección y el sentido.
Es importante destacar que al sumar vectores, estos deben representar una misma magnitud física, por lo tanto la suma vectorial es una operación homogénea. Esto significa que podemos sumar una fuerza con otra, pero no una fuerza con un desplazamiento, ya que el resultado carece de sentido.
Se dispone de varios métodos para encontrar el vector resultante: gráficos y analíticos. Para encontrar sumas vectoriales con métodos gráficos se parte de una representación sencilla para un vector, a saber, un segmento orientado o flecha como esta:
Los vectores se denotan mediante letras negritas en texto impreso, o con una flecha por encima de la letra, para distinguirlos de sus respectivas magnitudes o de las cantidades escalares. Por ejemplo, la magnitud del vector ves simplemente v.
Índice del artículo
Para sumar más de dos vectores coplanares se utiliza el método del polígono o método de la poligonal, que consiste en trasladar paralelamente a sí mismo a cada uno de los vectores sumandos. Una característica de los vectores es que son invariantes respecto a la traslación, por lo tanto nos valdremos de esta propiedad para establecer la suma.
Se comienza con cualquiera de los vectores, ya que la adición vectorial es conmutativa y el orden de los sumandos no altera la suma. El segundo vector se traslada a continuación, haciendo coincidir su origen con el extremo del primero.
Después se trae al siguiente vector y se pone a continuación, siguiendo el mismo procedimiento, que es hacer coincidir el origen con el extremo del anterior. Se procede de esta manera hasta posicionar al último vector.
El vector resultante es el que une el origen del primero con el extremo libre del último. El nombre de este método proviene de la figura que resulta: un polígono.
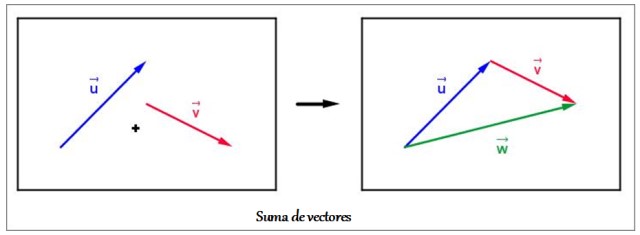
Tomemos como ejemplo la suma de dos vectores u y v que se muestra en la figura superior.
Comenzando por el vector u, se trasladó al vector v para hacer coincidir su origen con el extremo del primero. El vector resultante w se dibuja desde el origen de u hasta el extremo de v, formando una figura de tres lados: un triángulo. Por eso en este caso especial, al procedimiento se lo llama método del triángulo.
Nótese un detalle importante, la magnitud o módulo del vector resultante no es la suma de los módulos de los vectores sumandos. De hecho, casi siempre es menor, salvo que los vectores sean paralelos.
Veamos a continuación lo que sucede en este caso.
El método descrito se puede aplicar también al caso especial en que los vectores son paralelos. Consideremos el siguiente ejemplo:
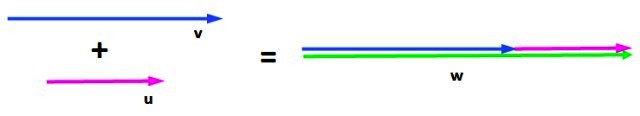
Se deja al vector v en su posición original, y se traslada al vector u de tal forma que su origen concuerde con el extremo de v. Ahora se traza un vector que comienza desde el origen de v y termina el extremo de u.
Este es el vector resultante w y su tamaño es la suma de los tamaños de los sumandos. La dirección y el sentido de los tres vectores es el mismo.
El vector resultante tiene módulo máximo si los sumandos forman entre sí un ángulo de 0º, como los del ejemplo. Si los vectores forman ángulo de 180º entre sí, entonces el vector resultante tiene módulo mínimo.
Un ciclista recorre primero 3 km dirigiéndose hacia el norte y después 4 km hacia el oeste. Su desplazamiento, al que llamamos R, se encuentra fácilmente con el método del triángulo más un sistema de referencia, donde se marcan los puntos cardinales:
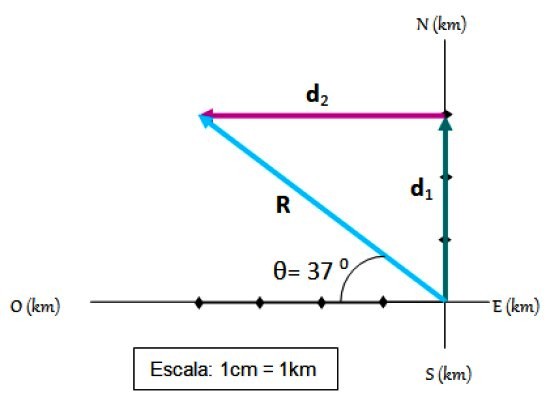
Pasos para sumar vectorialmente
-El punto de partida se hace coincidir con el origen del sistema de referencia.
-Sobre los ejes coordenados se escoge una escala, que en este caso es 1 cm = 1 km
-Se dibuja a escala el primer desplazamiento d1.
-Seguidamente a d1 se dibuja el segundo desplazamiento d2, también a escala.
-El desplazamiento resultante R es un vector que va desde el origen hasta el extremo de d2.
-El tamaño de R se mide con una regla graduada, es fácil comprobar que R = 5.
-Por último el ángulo que R forma con la horizontal se mide con ayuda de un transportador y resulta ser θ= 37 0
Un nadador quiere atravesar un río y para ello nada a una velocidad de 6 km/h, perpendicularmente a la orilla, pero una corriente que lleva velocidad de 4 km/h lo desvía.
Para conocer su velocidad resultante se suman los vectores de velocidad del nadador, que se ha dibujado vertical y de la corriente, que se muestra horizontal.
Siguiendo el método gráfico se obtiene la velocidad resultante vR:
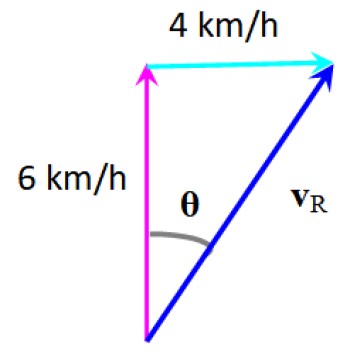
La desviación que experimenta el nadador se puede calcular mediante:
θ = arctg (4/6) = 33.7º a la derecha de su dirección inicial
La magnitud de su velocidad se ve incrementada gracias a que la velocidad del río se suma vectorialmente. Se puede encontrar estableciendo cuidadosamente una escala, como en el ejemplo anterior.
O bien con ayuda de las razones trigonométricas de 33.7º:
sen 33.7º = 4/vR
vR = 4/ sen 33.7º = 7.21 km/h
Sobre una partícula actúan las siguientes fuerzas, cuyas magnitudes se listan a continuación:
F1=2.5 N; F2=3 N; F3=4 N; F4=2.5 N
Encontrar la fuerza resultante.
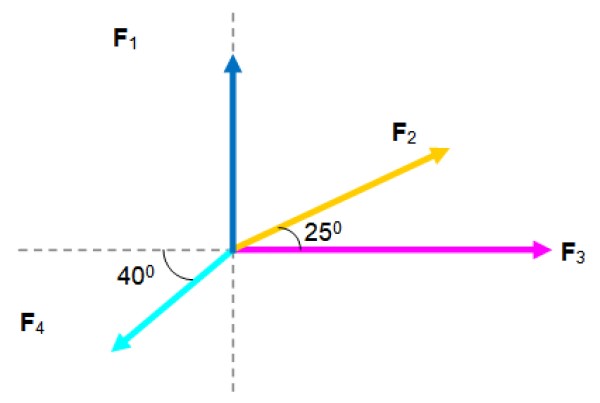
Podemos sumar gráficamente comenzando con cualquiera de los vectores, ya que la suma vectorial es conmutativa.
En la figura A se comenzó con F1. Estableciendo una escala y con ayuda de regla y escuadra se trasladan los demás vectores para colocarlos uno después del otro.
El vector FR está dirigido desde el origen de F1 hasta el extremo de F4. Su magnitud es 5.2 N y forma un ángulo de 26.5º con respecto a la horizontal.
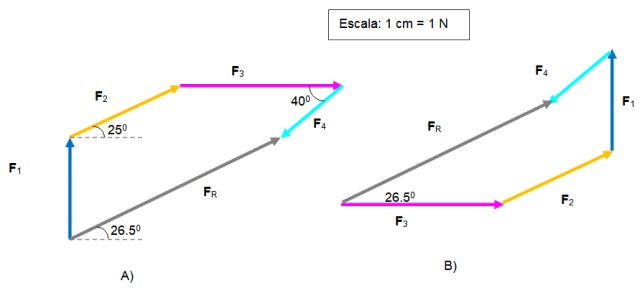
En la figura B se resolvió el mismo problema, comenzando con F3 y terminando con F4, para obtener igual FR .
Los polígonos son diferentes, pero el resultado es el mismo. El lector puede hacer la prueba cambiando nuevamente el orden de los vectores.
- Bauer, W. 2011. Física para Ingeniería y Ciencias. Volumen 1. Mc Graw Hill.
- Bedford, 2000. A. Mecánica para Ingeniería: Estática. Addison Wesley.
- Figueroa, D. (2005). Serie: Física para Ciencias e Ingeniería. Volumen 1. Cinemática. Editado por Douglas Figueroa (USB).
- Giambattista, A. 2010. Physics. 2nd. Ed. McGraw Hill.
- Sears, Zemansky. 2016. University Physics with Modern Physics. 14th. Ed. Volume 1.
