Velocidad angular media: definición y fórmulas, ejercicios resueltos
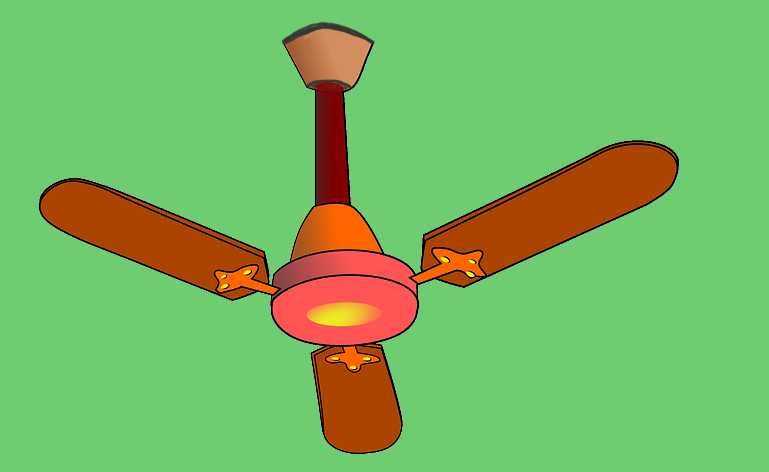
La velocidad angular media de rotación se define como el ángulo girado por unidad de tiempo del vector posición de un punto que describe movimiento circular. Las aspas de un ventilador de techo (como el mostrado en la figura 1), siguen movimiento circular y su velocidad angular media de giro se calcula tomando el cociente entre el ángulo girado y el tiempo en que se recorrió ese ángulo.
Las reglas que sigue el movimiento de rotación son de cierta manera semejantes a las ya familiares del movimiento traslacional. Las distancias recorridas pueden medirse en metros también, sin embargo las magnitudes angulares cobran especial relevancia porque facilitan en gran medida la descripción del movimiento.
Por lo general se utilizan letras griegas para las magnitudes angulares y letras latinas para las correspondientes magnitudes lineales.
Índice del artículo
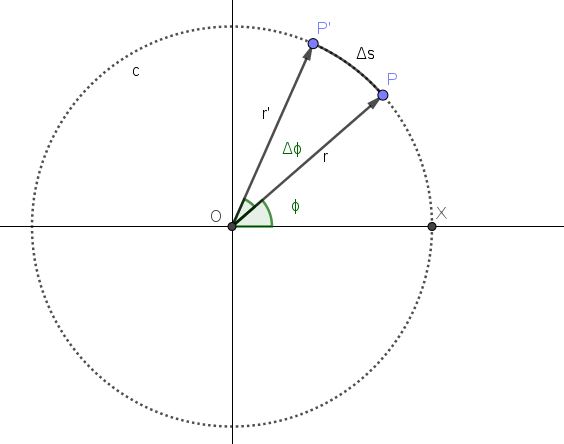
En la figura 2 se representa el movimiento de un punto sobre una trayectoria circular c. La posición P del punto corresponde al instante t y la posición angular correspondiente a ese instante es ϕ.
A partir del instante t transcurre un lapso de tiempo Δt. En ese lapso la nueva posición del punto es P’ y la posición angular se ha incrementando un ángulo Δϕ.
La velocidad angular media ω es el ángulo recorrido por unidad de tiempo, de modo que el cociente Δϕ/Δt representará la velocidad angular media entre los instantes t y t+Δt:
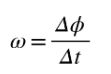
Como el ángulo se mide en radianes y el tiempo en segundos, la unidad de la velocidad angular media es rad/s. Si se quiere calcular la velocidad angular justo en el instante t, entonces habrá que calcular el cociente Δϕ/Δt cuando Δt ➡0.
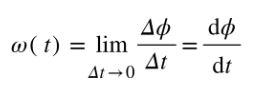
Un movimiento de rotación es uniforme si en cualquier instante observado, el ángulo recorrido es el mismo en el mismo lapso de tiempo. Si la rotación es uniforme, entonces la velocidad angular en cualquier instante coincide con la velocidad angular media.
En un movimiento de rotación uniforme el tiempo en el que se da una vuelta completa se llama el periodo y se denota con T.
Además, cuando se da una vuelta completa el ángulo recorrido es 2π, por eso en una rotación uniforme la velocidad angular ω se relaciona con el periodo T, mediante la siguiente fórmula:
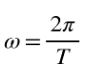
Se define la frecuencia f de una rotación uniforme como el cociente entre el número de vueltas y el tiempo empleado en recorrerlas, es decir si en el lapso de tiempo Δt se dan N vueltas entonces la frecuencia será:
f= N/Δt
Como una vuelta (N=1) se recorre en un tiempo T (el periodo), se tiene la siguiente relación:
f = 1/T
Es decir, en una rotación uniforme la velocidad angular se relaciona con la frecuencia mediante la relación:
ω = 2π・f
Relación entre rapidez angular y rapidez lineal
La rapidez lineal v, es el cociente entre la distancia recorrida y el lapso de tiempo empleado en recorrerla. En la figura 2 la distancia recorrida es la longitud del arco Δs.
El arco Δs es proporcional al ángulo recorrido Δϕ y al radio r, cumpliéndose la siguiente relación:
Δs = r・Δϕ
Siempre que Δϕ esté medido en radianes.
Si dividimos la expresión anterior entre el lapso de tiempo Δt obtendremos:
(Δs/Δt) = r・(Δϕ/Δt)
El cociente del primer miembro es la rapidez lineal y el cociente del segundo miembro la velocidad angular media:
v = r・ω
Las puntas de las aspas del ventilador de techo mostrado en la figura 1 se mueven con una rapidez de 5 m/s y las aspas tienen 40 cm de radio.
Con estos datos calcule: i) la velocidad angular media de la rueda, ii) el número de vueltas que da la rueda en un segundo, iii) el periodo en segundos.
Solución
i) La rapidez lineal es v=5 m/s.
El radio es r= 0,40 m.
De la relación entre rapidez lineal y rapidez angular despejamos esta última:
v = r・ω => ω = v/r = (5 m/s)/(0,40 m) = 12,57 rad/s
ii) ω = 2π・f => f = ω / 2π = (12,57 rad/s) / ( 2π rad) = 2 vuelta/s
iii) T= 1 / f = 1 / (2 vuelta/s) = 0,5 s por cada vuelta.
Un cochecito de juguete se mueve en una pista circular de 2m de radio. A los 0s su posición angular es 0 rad, pero al cabo de un tiempo t su posición angular es
φ(t) = 2・t .
Con estos datos
i) Calcule la velocidad angular media en los siguiente intervalos de tiempo [0s, 0.5s]; [0.5s, 1.0s]; [1.0s, 1.5s] y por último en el lapso [0.0s, 1.5s].
ii) En base a los resultados de la parte i) ¿Qué se puede decir del movimiento?
iii) Determine la rapidez lineal media en los mismos lapso de tiempo del apartado i)
iv) Halle la velocidad angular y la rapidez lineal para cualquier instante.
Solución
i) La velocidad angular media está dada por la siguiente fórmula:
Procedemos a calcular el ángulo recorrido y el lapso de tiempo transcurrido en cada intervalo.
Intervalo 1: Δϕ= ϕ(0.5s) – ϕ(0.0s)= 2(rad/s)*0.5s – 2(rad/s)*0.0s= 1.0 rad
Δt= 0.5s – 0.0s= 0.5s
ω= Δϕ/Δt= 1.0rad/0.5s= 2.0 rad/s
Intervalo 2: Δϕ= ϕ(1.0s) – ϕ(0.5s)= 2(rad/s)*1.0s – 2(rad/s)*0.5s= 1.0 rad
Δt= 1.0s – 0.5s= 0.5s
ω= Δϕ/Δt= 1.0rad/0.5s= 2.0 rad/s
Intervalo 3: Δϕ= ϕ(1.5s) – ϕ(1.0s)= 2(rad/s)*1.5s – 2(rad/s)*1.0s= 1.0 rad
Δt= 1.5s – 1.0s= 0.5s
ω= Δϕ/Δt= 1.0rad/0.5s= 2.0 rad/s
Intervalo 4: Δϕ= ϕ(1.5s) – ϕ(0.0s)= 2(rad/s)*1.5s – 2(rad/s)*0.0s= 3.0 rad
Δt= 1.5s – 0.0s= 1.5s
ω= Δϕ/Δt= 3.0rad/1.5s= 2.0 rad/s
ii) En vista de los resultados anteriores, en los que se calculó la velocidad angular media en distintos intervalos de tiempo obteniéndose siempre el mismo resultado parece indicar que se trata de un movimiento circular uniforme. Sin embargo estos resultados no son concluyentes.
La forma de asegurar la conclusión es calcular la velocidad angular media para un intervalo arbitrario [t, t’]: Δϕ= ϕ(t’) – ϕ(t)= 2*t’ – 2*t= 2*(t’-t)
Δt= t’ – t
ω= Δϕ/Δt= 2*(t’-t)/(t’-t) = 2.0 rad/s
Esto significa que el cochecito de juguete tiene velocidad angular media constante de 2 rad/s en cualquier lapso de tiempo considerado. Pero puede irse más allá si se calcula la velocidad angular instantánea:
Esto se interpreta como que el auto de juguete en todo instante tiene velocidad angular constante = 2 rad/s.
- Giancoli, D. Physics. Principles with Applications. 6th Edition. Prentice Hall. 30- 45.
- Kirkpatrick, L. 2007. Física: Una mirada al mundo. 6ta Edición abreviada. Cengage Learning. 117.
- Resnick, R. (1999). Física. Volumen 1. Tercera edición en español. México. Compañía Editorial Continental S.A. de C.V. 33-52.
- Serway, R., Jewett, J. (2008). Física para Ciencias e Ingeniería. Volumen 1. 7ma. Edición. México. Cengage Learning Editores. 32-55.
- Wikipedia. Velocidad angular. Recuperado de: wikipedia.com
