Función constante: características, ejemplos, ejercicios
La función constante es aquella en la que se mantiene constante el valor de y. Dicho de otra forma: una función constante siempre tiene la forma f(x) = k, donde k es un número real.
Al graficar la función constante en el sistema de coordenadas xy, siempre resulta una línea recta paralela al eje horizontal o eje de las x.
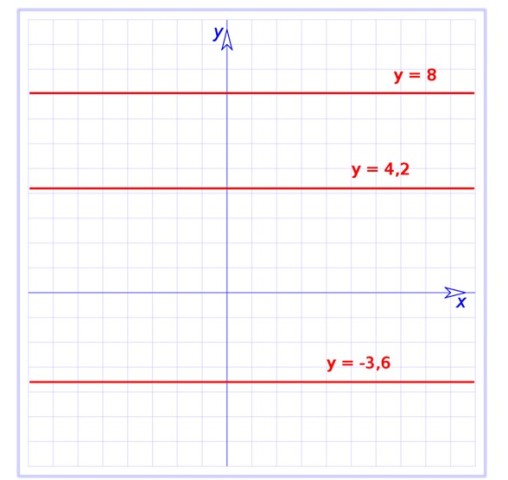
Esta función es un caso particular de la función afín, cuya gráfica es también una línea recta, pero con pendiente. La función constante tiene pendiente nula, es decir, es una recta horizontal, tal como se aprecia en la figura 1.
Allí se muestra la gráfica de tres funciones constantes:
f(x) = -3.6
g(x) = 4.2
h(x) = 8
Todas son rectas paralelas al eje horizontal, la primera de ellas se encuentra por debajo de dicho eje, mientras que las restantes están por encima.
Índice del artículo
Podemos resumir las principales características de la función constante de la siguiente forma:
-Su gráfica es una línea recta horizontal.
-Posee intersección única con el eje y, que vale k.
-Es continua.
-El dominio de la función constante (el conjunto de valores que puede tener la x) es el conjunto de los números reales R.
-El recorrido, rango o contradominio (el conjunto de valores que toma la variable y) es simplemente la constante k.
Las funciones son necesarias para establecer vínculos entre magnitudes que dependen entre sí de alguna forma. La relación existente entre ellas puede modelarse matemáticamente, para saber cómo se comportan una de ellas cuando varía la otra.
Esto ayuda a construir modelos para muchas situaciones y hacer predicciones acerca de su comportamiento y evolución.
Pese a su aparente simplicidad, la función constante tiene muchas aplicaciones. Por ejemplo, cuando se trata de estudiar magnitudes que permanecen constantes en el tiempo, o por lo menos, durante un tiempo apreciable.
De esta forma se comportan magnitudes en situaciones como las siguientes:
-La velocidad de crucero de un coche que se mueve por una larga autopista rectilínea. Mientras no frene o acelere, el auto lleva un movimiento rectilíneo uniforme.

-Un condensador totalmente cargado y desconectado de un circuito, tiene una carga constante en el tiempo.
-Finalmente, un estacionamiento con tarifa plana, mantiene un precio constante sin importar cuanto tiempo se pase un coche estacionado allí.
La función constante alternativamente se puede representar de la siguiente manera:
f(x) = kx0
Puesto que cualquier valor de x elevado a la 0 da 1 como resultado, la expresión anterior se reduce a la ya familiar:
f(x) = k
Desde luego eso ocurre siempre y cuando el valor de k sea diferente de 0.
Por eso también se clasifica a la función constante como una función polinomial de grado 0, ya que el exponente de la variable x es 0.
Responda las siguientes preguntas:
a) ¿Se puede afirmar que la recta dada por x = 4 es una función constante? Razone su respuesta.
b) ¿Una función constante puede tener intersección con el eje x?
c) ¿Es constante la función f(x)=w2?
Respuesta a
He aquí la gráfica de la recta x = 4:
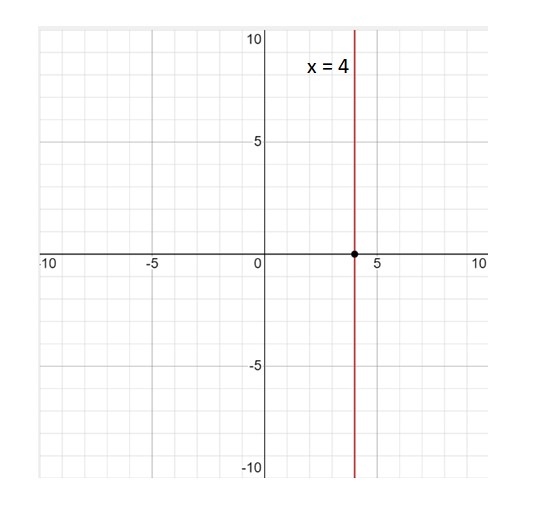
La recta x = 4 no es una función; por definición una función es una relación tal que a cada valor de la variable x le corresponde un único valor de y. Y en este caso esto no se cumple, ya que el valor x = 4 está asociado a infinitos valores de y. Por lo tanto la respuesta es no.
Respuesta b
En general una función constante no tiene intersección con el eje x, a menos que se trate de y = 0, en cuyo caso se trata del eje x propiamente dicho.
Respuesta c
Sí, puesto que w es constante, su cuadrado también lo es. Lo que interesa es que w no dependa de la variable de entrada x.
Encuentre la intersección entre las funciones f(x) = 5 y g(x) = 5x – 2
Solución
Para hallar la intersección entre estas dos funciones se pueden reescribir respectivamente como:
y = 5; y = 5x – 2
Se igualan, obteniéndose:
5x – 2 = 5
Que es una ecuación lineal de primer grado, cuya solución es:
5x = 5+2 = 7
x = 7/5
El punto de intersección es (7/5; 5).
Demuestre que la derivada de una función constante es 0.
Solución
De la definición de derivada se tiene:
f(x+h) = k
Sustituyendo en la definición:
Además, si pensamos en la derivada como tasa de cambio dy/dx, la función constante no experimenta cambio alguno, por lo tanto su derivada es nula.
Encuentre la integral indefinida de f(x) = k.
Solución
Una compañía de telefonía celular ofrece servicio de Internet ilimitado con tarifa plana pagando 15 $ al mes. ¿Cuál es la función de precio según el tiempo?
Solución
Sea P el precio a pagar en $ y t el tiempo, que se puede expresar en días. La función se establece así:
P(t) = 15
El siguiente gráfico de velocidad versus tiempo corresponde al movimiento de una partícula.
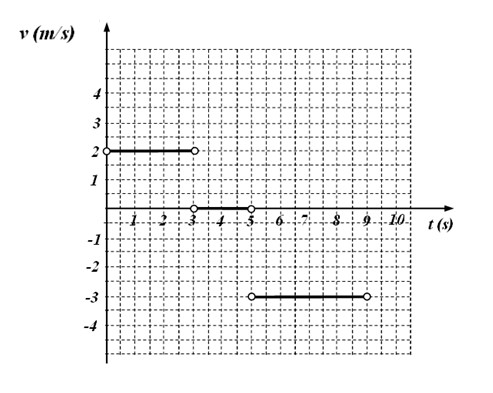
Se pide:
a) Escribir una expresión para la función velocidad en función del tiempo v(t).
b) Encontrar la distancia recorrida por el móvil en el intervalo de tiempo comprendido entre 0 y 9 segundos.
Solución a
Del gráfico mostrado se aprecia que:
–v = 2 m/s en el intervalo de tiempo comprendido entre 0 y 3 segundos
-El móvil está detenido entre 3 y 5 segundos, ya que en dicho intervalo la velocidad vale 0.
–v = – 3 m/s entre 5 y 9 segundos.
Es un ejemplo de una función a trozos, o función por partes, que a su vez está compuesta de funciones constantes, válidas únicamente para los intervalos de tiempo señalados. Se concluye que la función buscada es:

Solución b
A partir de la gráfica v(t) se puede calcular la distancia recorrida por el móvil, que equivale numéricamente al área bajo/sobre la curva. De esta manera:
-Distancia recorrida entre 0 y 3 segundos = 2 m/s . 3 s = 6 m
-Entre 3 y 5 segundos estuvo detenido, por lo tanto no recorrió distancia alguna.
-Distancia recorrida entre 5 y 9 segundos = 3 m/s . 4 s = 12 m
En total el móvil recorrió 18 m. Véase que aunque la velocidad es negativa en el intervalo entre 5 y 9 segundos, la distancia recorrida es positiva. Lo que sucede es que durante ese intervalo de tiempo, el móvil había cambiado el sentido de su velocidad.
- Geogebra. Funciones constantes. Recuperado de: geogebra.org.
- Maplesoft. The Constant Function. Recuperado de: maplesoft.com.
- Wikilibros. Cálculo en una variable/Funciones/Función Constante. Recuperado de: es.wikibooks.org.
- Wikipedia. Constant function. Recuperado de: en.wikipedia.org
- Wikipedia. Función constante. Recuperado de: es.wikipedia.org.
