Identidades pitagóricas: demostración, ejemplo, ejercicios

Son identidades pitagóricas todas las ecuaciones trigonométricas que se cumplen para cualquier valor del ángulo y están fundamentadas en el teorema de Pitágoras. La más famosa de las identidades pitagóricas es la identidad trigonométrica fundamental:

Sen²(α) + Cos²(α) = 1

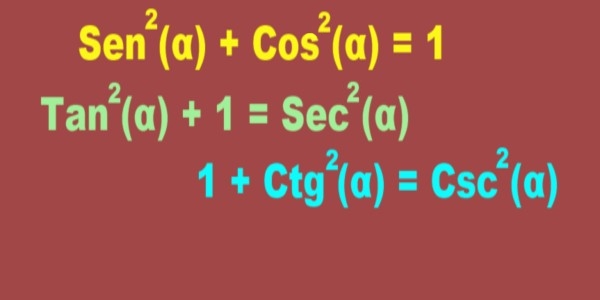
Le sigue en importancia y uso la identidad pitagórica de la tangente y la secante:

Tan²(α) + 1 = Sec²(α)

Y la identidad trigonométrica pitagórica que involucra a la cotangente y a la cosecante:

1 + Ctg²(α) = Csc²(α)

Índice del artículo

• 1 Demostración
  • 1.1 El seno y el coseno
  • 1.2 La identidad fundamental
  • 1.3 El eje de la tangente
  • 1.4 La identidad pitagórica de la tangente
• 2 Ejemplo
• 3 Ejercicios resueltos
  • 3.1 Ejercicio 1
  • 3.2 Ejercicio 2
• 4 Referencias

Demostración

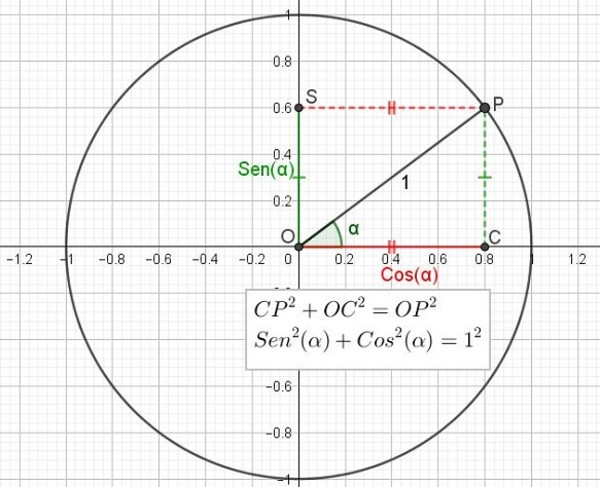
Las razones trigonométricas seno y coseno se representan en una circunferencia de radio uno (1) conocida como círculo trigonométrico. Dicho círculo tiene centro en el origen de coordenadas O.

Los ángulos se miden a partir del semieje positivo de las X, por ejemplo el ángulo α en la figura 2 (ver más adelante). En sentido contrario a las manecillas del reloj si el ángulo es positivo, y en la dirección de las manecillas si se trata de un ángulo negativo.

Se traza la semirrecta con origen O y ángulo α, la cual intercepta al círculo unitario en el punto P. El punto P se proyecta ortogonalmente sobre el eje horizontal X dando lugar al punto C. Similarmente P se proyecta perpendicularmente sobre el eje vertical Y dando lugar al punto S.

Se tiene el triángulo OCP rectángulo en C. 

El seno y el coseno

Debe recordarse que la razón trigonométrica seno se define sobre un triángulo rectángulo de la siguiente manera:

El seno de un ángulo del triángulo es la razón o cociente entre el cateto opuesto al ángulo y la hipotenusa del triángulo.

Aplicado al triángulo OCP de la figura 2 quedaría así:

Sen(α) = CP / OP

pero CP = OS y OP =1, de modo que:

Sen(α) = OS

Lo que significa que la proyección OS sobre el eje Y tiene un valor igual al del seno del ángulo mostrado. Debe notarse que el máximo valor del seno de un ángulo (+1) ocurre cuando α = 90º y el mínimo (-1) cuando α = -90º o α = 270º.

De forma similar el coseno de un ángulo es el cociente entre el cateto adyacente al ángulo y la hipotenusa del triángulo.

Aplicado al triángulo OCP de la figura 2 quedaría así:

Cos(α) = OC / OP

pero OP =1, de modo que:

Cos(α) = OC

Lo que significa que la proyección OC sobre el eje X tiene un valor igual al del seno del ángulo mostrado. Debe notarse que el máximo valor del coseno (+1) ocurre cuando α = 0º o α = 360º, mientras que el mínimo valor del coseno es (-1) cuando α = 180º.

La identidad fundamental

Para el triángulo OCP rectángulo en C se aplica el teorema de Pitágoras, el cual afirma que la suma del cuadrado de los catetos es igual al cuadrado de la hipotenusa:

CP² + OC² = OP²

Pero ya se ha dicho que CP = OS = Sen(α), que OC = Cos(α) y que OP = 1, por lo que la expresión anterior puede ser reescrita en función del seno y del coseno del ángulo:

Sen²(α) + Cos²(α) = 1

El eje de la tangente

Así como el eje X en el círculo trigonométrico es el eje del coseno y el eje Y el eje del seno, de igual forma existe el eje de la tangente (ver figura 3) el cual es precisamente la recta tangente al círculo unitario en el punto B de coordenadas (1, 0). 

Si se quiere saber el valor de la tangente de un ángulo, se traza el ángulo a partir del semieje positivo de las X, la intersección del ángulo con el eje de la tangente define un punto Q, la longitud del segmento OQ es la tangente del ángulo.

Esto es porque por definición, la tangente del ángulo α es el cateto opuesto QB entre el cateto adyacente OB. Es decir Tan(α) = QB / OB = QB / 1 = QB.

La identidad pitagórica de la tangente

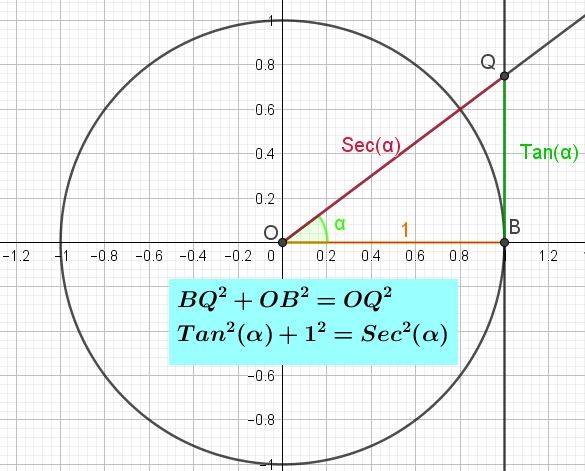
Puede demostrarse la identidad pitagórica de la tangente si se considera el triángulo OBQ rectángulo en B (figura 3). Aplicando el teorema de Pitágoras a dicho triángulo se tiene que BQ² + OB² = OQ². Pero ya se ha dicho que BQ = Tan(α), que OB = 1 y que OQ = Sec(α), de modo que sustituyendo en la igualdad de Pitágoras para el triángulo rectángulo OBQ se tiene:

Tan²(α) + 1 = Sec²(α).

Ejemplo

Verifique si se cumplen o no las identidades pitagóricas en el triángulo rectángulo de catetos AB = 4 y BC = 3.

Solución: Se conocen los catetos, falta determinar la hipotenusa, la cual es:

AC = √( AB^2 + BC^2) = √( 4^2 + 3^2) = √( 16 + 9) = √(25) = 5.

Al ángulo ∡BAC se le llamará α, ∡BAC = α. Ahora se determinan las razones trigonométricas:

Sen α = BC / AC = 3/5 

Cos α = AB / AC = 4/5 

Tan α = BC / AB = 3/4 

Cotan α = AB / BC = 4/3 

Sec α = AC / AB = 5/4 

Csc α = AC / BC = 5/3

Se comienza por la identidad trigonométrica fundamental:

Sen²(α) + Cos²(α) = 1

(3/5)^2 + (4/5)^2 = 9/25 + 16/25 = (9 +16)/25 = 25/25 = 1

Se concluye que se cumple.

– La próxima identidad pitagórica es la de la tangente:

Tan²(α) + 1 = Sec²(α)

(3/4)^2 + 1 = 9/16 + 16/16 = (9+16)/16 = 25/16 = (5/4)^2

Y se concluye que se verifica la identidad de la tangente.

– De modo similar la de la cotangente:

1 + Ctg²(α) = Csc²(α)

1+ (4/3)^2 = 1 + 16/9 = 25/9 = (5/3)^2

Se concluye que también se cumple, con lo que se ha completado la tarea de verificar las identidades pitagóricas para el triángulo dado.

Ejercicios resueltos

Probar las siguientes identidades, fundamentándose en las definiciones de las razones trigonométrica y las identidades pitagóricas.

Ejercicio 1

Probar que Cos² x = (1 + Sen x) (1 – Sen x).

Solución: En el miembro derecho se reconoce el producto notable de la multiplicación de un binomio por su conjugado el cual, como se sabe, es una diferencia de cuadrados:

Cos² x  = 1² – Sen² x

Luego el término con seno en el lado derecho pasa al lado izquierdo con el signo cambiado:

Cos² x + Sen² x = 1

Notándose que se ha llegado a la identidad trigonométrica fundamental, por lo que se concluye que la expresión dada es una identidad, es decir se cumple para cualquier valor de x.

Ejercicio 2

Partiendo de la identidad trigonométrica fundamental y usando las definiciones de las razones trigonométricas demostrar la identidad pitagórica de la cosecante.

Solución: La identidad fundamental es:

Sen²(x) + Cos²(x) = 1

Se divide ambos miembros entre Sen²(x) y se distribuye el denominador en el primer miembro:

Sen²(x)/Sen²(x) + Cos²(x)/Sen²(x) = 1/Sen²(x)

Se simplifica:

1 + (Cos(x)/Sen(x))^2 = (1/Sen(x))^2

Cos(x)/Sen(x) = Cotan(x) es una identidad (no pitagórica) que se verifica por la propia definición de las razones trigonométricas. De igual manera ocurre con la siguiente identidad: 1/Sen(x) = Csc (x).

Finalmente se tiene que:

1 + Ctg²(x) = Csc²(x)

Referencias

1. Baldor J. (1973). Geometría plana y del espacio con una introducción a la trigonometría. Cultural Centroamericana. C.A.
2. C. E. A. (2003). Elementos de geometría: con ejercicios y geometría del compás. Universidad De Medellín.
3. Campos, F., Cerecedo, F. J. (2014). Matemáticas 2. Grupo Editorial Patria.
4. IGER. (s.f.). Matemática Primer Semestre Tacaná. IGER.
5. Jr. geometry. (2014). Polygons. Lulu Press, Inc.
6. Miller, Heeren, & Hornsby. (2006). Matemática: Razonamiento Y Aplicaciones (Décima Edición). Pearson Educación.
7. Patiño, M. (2006). Matemáticas 5. Editorial Progreso.
8. Wikipedia. Identidades y fórmulas de trigonometría. Recuperado de: es.wikipedia.com