Razones trigonométricas: ejemplos, ejercicios y aplicaciones
Las razones trigonométricas son los cocientes o razones que pueden hacerse con el valor de los lados de un triángulo rectángulo. Estos lados son: dos catetos que forman 90º entre sí y la hipotenusa, que forma el ángulo agudo θ con uno de los catetos.
Se pueden formar 6 cocientes. Sus nombres y respectivas abreviaturas son:
- seno (sen)
- coseno (cos)
- tangente (tg o tan)
- cotangente (ctg o cotan)
- secante (sec) y
- cosecante (cosec)
Todas ellas referidas ángulo θ, como se muestra en la siguiente figura:
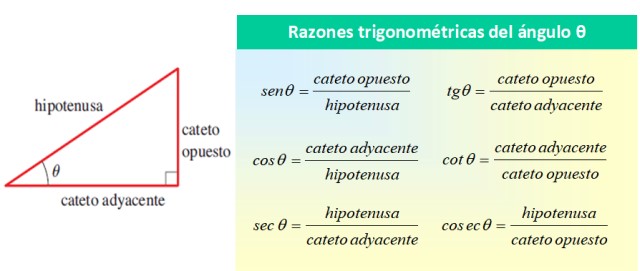
Las razones trigonométricas básicas del ángulo θ son sen θ, cos θ y tan θ, mientras que las restantes razones pueden expresarse en términos de estas tres. Del cuadro anterior se puede ver que:
- sec θ = 1/ cos θ
- cosec θ = 1/ sen θ
- cot θ = 1/tg θ
El tamaño de los lados del triángulo no influye en el valor de las razones, ya que dos triángulos cuyos ángulos miden lo mismo son triángulos semejantes y los respectivos cocientes entre los lados tienen el mismo valor.
Índice del artículo
Por ejemplo, calculemos las razones trigonométricas del ángulo θ en los siguientes triángulos:
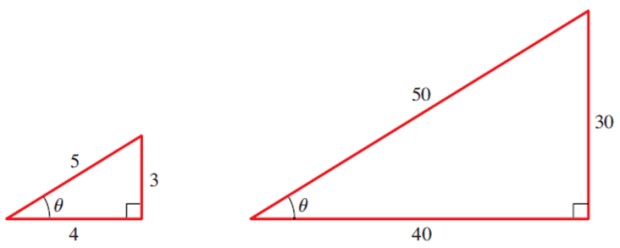
Para el triángulo pequeño tenemos las tres razones básicas del ángulo θ:
sen θ = 3/5
cos θ = 4/5
tg θ = ¾
Y ahora calculemos las tres razones básicas de θ con el triángulo grande:
sen θ = 30/50 =3/5
cos θ = 40/50 = 4/5
tg θ = 30/40 = ¾
Un detalle importante a tener en cuenta es el siguiente: tanto sen θ como cos θ son menores que 1, ya que los catetos siempre miden menos que la hipotenusa. En efecto:
sen θ = 3/5 = 0.6
cos θ = 4/5 = 0.8
En los siguientes ejercicios se pide resolver el triángulo rectángulo, lo cual significa encontrar la longitud de sus tres lados y la medida de sus ángulos internos, uno de los cuales siempre mide 90º.
El teorema de Pitágoras se aplica a los triángulos rectángulos y es muy útil cuando se conocen dos de los lados y hay que determinar el faltante. El teorema dice así:
Hipotenusa2 = cateto opuesto2 + cateto adyacente2
Podemos comprobar el teorema de Pitágoras con el triángulo pequeño de la figura 2, cuyos catetos son 3 y 4. El orden en que se tomen los catetos no importa. Aplicando el teorema tenemos:
Hipotenusa2 = 32 + 42 = 9 + 16 = 25
Por lo tanto la hipotenusa es:
Hipotenusa = √25 = 5
Calcular las razones trigonométricas de los ángulos mostrados en los siguientes triángulos:
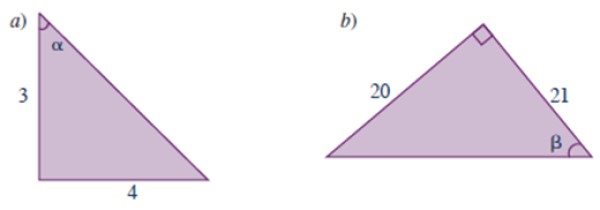
Solución a
Este triángulo es el mismo de la figura 3, pero nos piden las razones trigonométricas del otro ángulo agudo, denotado α. El enunciado no ofrece el valor de la hipotenusa, sin embargo, por aplicación del teorema de Pitágoras sabemos que vale 5.
Las razones se pueden calcular directamente de la definición, teniendo cuidado al seleccionar el cateto que sea el opuesto al ángulo α para calcular el sen α. Veamos:
- sen α = 4/5
- cos α = 3/5
- tg α = 4/3
- cot α = ¾
- sec α = 1 / (3/5) = 5/3
- cosec α = 1 / (4/5) = 5/4
Y como podemos ver, los valores de las razones trigonométricas se han intercambiado. En efecto, α y θ son ángulos complementarios, lo cual significa que suman 90º. En este caso se cumple que sen α = cos θ y así sucesivamente para las demás razones.
Solución b
Calculemos la hipotenusa del triángulo mediante el teorema de Pitágoras:
Hipotenusa2 = 202 + 212 = 841
√841 = 29
Entonces las 6 razones trigonométricas del ángulo β son:
- sen β = 20/29
- cos β = 21/29
- tg β = 20/21
- cot β = 21/20
- sec β = 1 / (21/29) = 29/21
- cosec β = 1 / (20/29) = 20/29
a) Encontrar el valor de x en la figura.
b) Calcular el perímetro de los 3 triángulos mostrados.
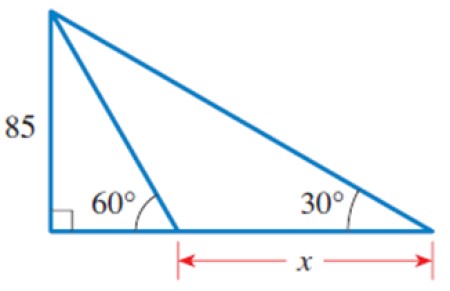
Solución a
En la figura podemos identificar varios triángulos, en particular el triángulo rectángulo de la izquierda, que tiene un cateto igual a 85 y el ángulo agudo 60º.
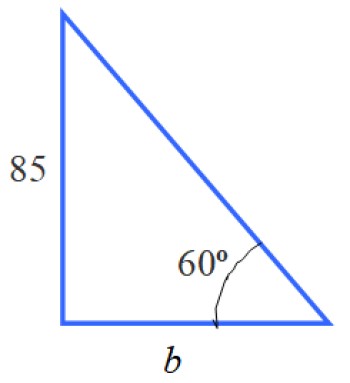
Con la información de este triángulo podemos calcular el lado b. No es la medida que pide el enunciado, pero conocer su valor es un paso previo.
Para determinarlo la razón apropiada es tg 60 º = 85 /b, ya que b es el cateto adyacente a 60 º y 85 es el opuesto a dicho ángulo. Por lo tanto:
b = 85 / tg 60º = 85 / √3
Una vez conocido b, usaremos el triángulo rectángulo grande y exterior, que tiene un lado común con el triángulo anterior: el que mide 85. Este es el cateto opuesto al ángulo de 30º.
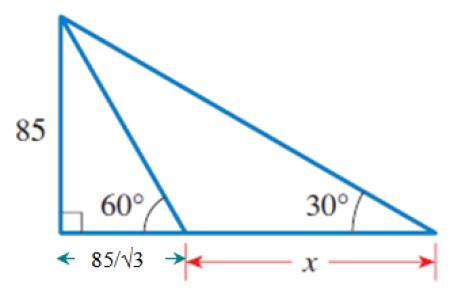
De allí:
Cateto adyacente a 30º= (85/√3) + x
Ahora podemos plantear lo siguiente:
85 / [(85/√3) + x] = tg 30º
Lo que está entre corchetes pasa a multiplicar la tg 30º:
85 = [(85/√3) + x]. tg 30º
Aplicando la propiedad distributiva de la multiplicación:
85 = tg 30º. (85/√3) + x. tg 30º
Por lo tanto:
x.tg 30º = 85 – tg 30º. (85/√3) = 85 [1 – tg 30º . (1/√3)] = 85 . (2/3) = 170/3
Sustituyendo el valor tg 30º = √3 / 3:
x = (170/3) ÷ (√3 / 3) = 98.15
Solución b
Perímetro del triángulo pequeño
Sea h1 la hipotenusa de este triángulo, que se puede calcular por teorema de Pitágoras o mediante una razón trigonométrica, por ejemplo cos 60º:
cos 60 º = 85/√3 / h1→ h1 = (85/√3) ÷ cos 60º = 98.1
Para hallar P, el perímetro de este triángulo, simplemente sumamos los 3 lados:
P = 85 + (85/√3) + 98.1 = 232.2
Perímetro del triángulo externo
Sea h2 a la hipotenusa del triángulo externo:
sen 30º = 85 ÷ h2
h2 = 85 ÷ sen 30º = 170
Para este triángulo el perímetro es:
P = 85 + [(85/√3) + 98.15] + 170 = 402.22
Perímetro del triángulo no rectángulo
De este triángulo ya conocemos todos sus lados:
P = x + h1 + h2 = 98.15 + 98.15 + 170 = 366.3
Las razones trigonométricas tienen numerosas aplicaciones prácticas, por ejemplo se pueden calcular alturas.
Supongamos que una torre de agua está a 325 pies de un edificio. Un observador situado en una ventana nota que el ángulo de elevación del extremo superior de la torre es de 39 º, mientras que el ángulo de depresión con que se mira la base de la torre es de 25º. Se pregunta:
a) ¿Cuál es la altura de la torre?
b) ¿A qué altura se sitúa la ventana?
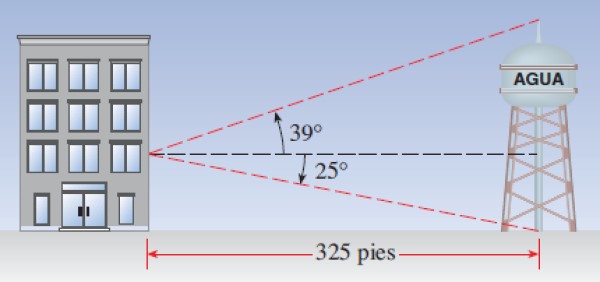
Solución a
Del cateto opuesto a 39 º del triángulo superior obtenemos una parte de la respuesta:
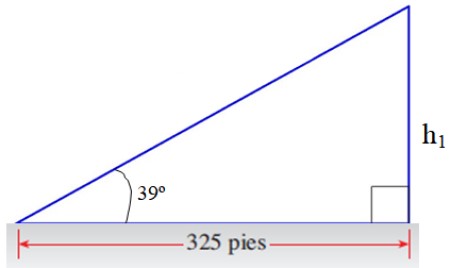
h1/325 = tg 39º → h1 = 325 . tg 39º pies = 263.2 pies
De manera semejante obtenemos el resto de la altura de la torre, llamado h2 a partir del triángulo inferior:
h2/325 = tg 25º → h2 = 325 . tg 25º pies = 151.6 pies
La altura total de la torre es h1 + h2 = 263.2 + 151.6 pies = 414.7 pies.
Solución b
La ventana está precisamente a una altura h2 del suelo:
h2 = 151.6 pies.
- Carena, M. 2019. Manual de Matemática Preuniversitaria. Universidad Nacional del Litoral.
- Hoffman, J. Selección de temas de Matemática. Volumen 3.
- Jiménez, R. 2008. Álgebra. Prentice Hall.
- Stewart, J. 2006. Precálculo: Matemáticas para el Cálculo. 5ta. Edición. Cengage Learning.
- Zill, D. 1984. Álgebra y Trigonometría. McGraw Hill.
