Estadística
2020-08-11T08:26:53+02:00

Chi-cuadrado (χ²): distribución, cómo se calcula, ejemplos

La prueba chi cuadrado o ji-cuadrado (χ², donde χ es la letra griega llamada “chi”) se utiliza para determinar el comportamiento de cierta variable y también cuando se quiere saber si dos o más variables son independientes estadísticamente.

Para comprobar el comportamiento de una variable, la prueba a realizar se llama prueba chi cuadrado de ajuste. Para saber si dos o más variables son independientes estadísticamente la prueba se llama chi cuadrado de independencia, también llamada de contingencia.

Estas pruebas forman parte de la teoría estadística de decisiones, en la cual se estudia una población y se toman decisiones acerca de esta, analizando una o varias muestras extraídas de ella. Para ello es preciso hacer ciertas suposiciones con respecto a las variables, llamadas hipótesis, las cuales pueden ser o no ciertas.

Hay algunas pruebas para contrastar estas conjeturas y determinar cuáles son válidas, dentro de un cierto margen de confianza, entre ellas la prueba chi-cuadrado, que puede aplicarse para comparar dos y más poblaciones.

Como veremos, suelen plantearse dos tipos de hipótesis acerca de algún parámetro poblacional en dos muestras: la hipótesis nula, llamada H_o (las muestras son independientes), y la hipótesis alternativa, denotada como H₁, (las muestras están correlacionadas) que es contraria de aquella.

Índice del artículo

1 ¿Cuándo se usa la prueba chi-cuadrado?
- 1.1 Condiciones para aplicarla
2 Distribución chi cuadrado
- 2.1 Grados de libertad
- 2.2 Formulación de las hipótesis
3 ¿Cómo se calcula la estadística chi-cuadrado?
- 3.1 Criterio de aceptación de Ho
4 Ejemplo de cálculo
5 Referencias

¿Cuándo se usa la prueba chi-cuadrado?

La prueba chi cuadrado se aplica a variables que describen cualidades, como por ejemplo sexo, estado civil, grupo sanguíneo, color de ojos y preferencias de diversos tipos.

La prueba está pensada cuando se desea:

-Comprobar si una distribución es apropiada para describir una variable, lo cual se denomina bondad del ajuste. Mediante la prueba de chi cuadrado se puede saber si hay diferencias significativas entre la distribución teórica seleccionada y la distribución de frecuencias observada.

-Conocer si dos variables X e Y son independientes desde el punto de vista estadístico. Esto se conoce como prueba de independencia.

Dado que se aplica a variables cualitativas o categóricas, la prueba chi cuadrado se utiliza ampliamente en ciencias sociales, administración y medicina.

Condiciones para aplicarla

Hay dos requerimientos importantes para aplicarla correctamente:

-Los datos deben estar agrupados en frecuencias.

-La muestra tiene que ser lo suficientemente grande para que sea válida la distribución chi cuadrado, de lo contrario su valor se sobreestima y da lugar al rechazo de la hipótesis nula cuando no debiera ser así.

La regla general es que si en los datos agrupados aparece una frecuencia con valor menor a 5, esta no se use. Si hay más de una frecuencia menor a 5, entonces deben combinarse en una para obtener una frecuencia con valor numérico mayor a 5.

Distribución chi cuadrado

χ² es una distribución continua de probabilidades. En realidad hay diferentes curvas, dependiendo de un parámetro k llamado grados de libertad de la variable aleatoria.

Sus propiedades son:

-El área bajo la curva es igual a 1.

-Los valores de χ² son positivos.

-La distribución es asimétrica, es decir, posee sesgo.

Grados de libertad

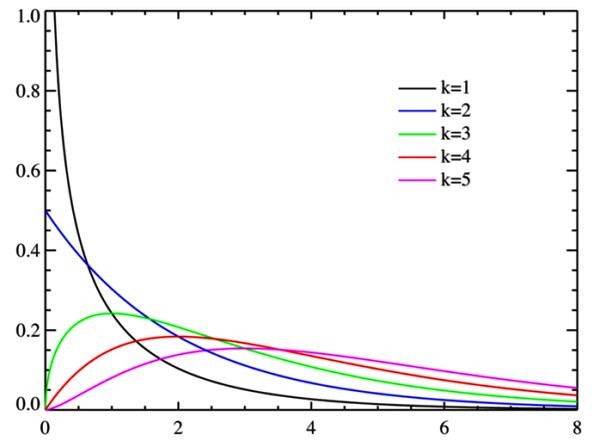
A medida que aumentan los grados de libertad, la distribución chi-cuadrado tiende a la normalidad, como se aprecia de la figura.

Para una distribución dada, los grados de libertad se determinan a través de la tabla de contingencia, que es la tabla donde se registran las frecuencias observadas de las variables.

Si una tabla tiene f filas y c columnas, el valor de k es:

k = (f – 1)⋅ (c – 1)

Formulación de las hipótesis

Cuando la prueba chi cuadrado es de ajuste, se formulan las siguientes hipótesis:

-H_o: la variable X tiene distribución de probabilidad f(x) con los parámetros específicos y₁, y₂…, y_p

-H₁: X tiene otra distribución de probabilidad.

La distribución de probabilidad que se supone en la hipótesis nula puede ser, por ejemplo, la conocida distribución normal, y los parámetros serían la media μ y la desviación estándar σ.

Además, la hipótesis nula es evaluada con un cierto nivel de significación, esto es, una medida del error que se cometería al rechazarla siendo cierta.

Por lo general este nivel se establece de 1%, 5 % o 10 % y cuanto menor sea, más fiable el resultado de la prueba.

Y si se utiliza la prueba chi cuadrado de contingencia, que como hemos dicho sirve para comprobar la independencia entre dos variables X e Y, las hipótesis son:

-H_o: las variables X e Y son independientes.

-H₁: X e Y son dependientes.

De nuevo se requiere especificar un nivel de significación para conocer la medida del error al tomar la decisión.

¿Cómo se calcula la estadística chi-cuadrado?

La estadística chi cuadrado se calcula de la siguiente manera:

La sumatoria se lleva a cabo desde la primera clase i = 1 hasta la última, que es i =k.

Además:

–f_o es una frecuencia observada (proviene de los datos obtenidos).

–f_e es la frecuencia esperada o teórica (es necesario calcularla a partir de los datos).

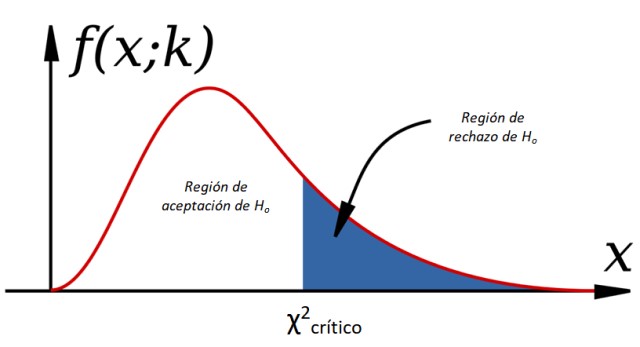
Para aceptar o rechazar la hipótesis nula, se calcula χ²para los datos observados y se compara con un valor llamado chi cuadrado crítico, el cual depende de los grados de libertad k y el nivel de significación α:

χ²_crítico=χ²_{k, α}

Si por ejemplo queremos realizar la prueba con un nivel de significación del 1 %, entonces α = 0.01, si va a ser con 5% entonces α = 0.05 y así sucesivamente. Se define p, el parámetro de la distribución, como:

p = 1 – α

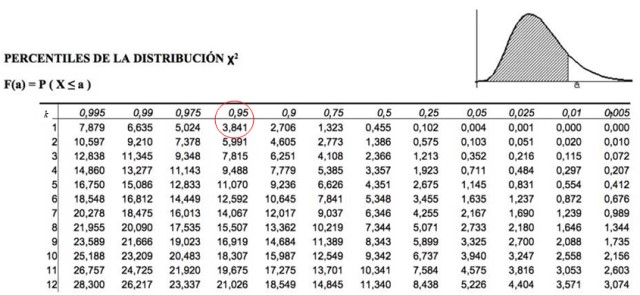
Estos valores de chi cuadrado crítico se determinan mediante tablas que contienen el valor del área acumulada. Por ejemplo, para k = 1, que representa 1 grado de libertad y α = 0.05, que equivale a p = 1- 0.05 = 0.95, el valor de χ² es 3.841.

Criterio de aceptación de H_o

El criterio para aceptar H_o es:

-Si χ² χ²_crítico se acepta H_o, de lo contrario se rechaza (ver figura 1).

Ejemplo de cálculo

En la siguiente aplicación se utilizará la prueba chi cuadrado como prueba de independencia.

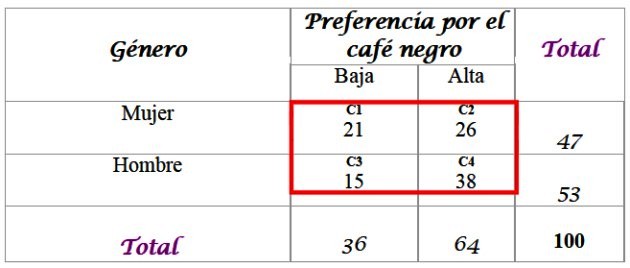
Supóngase que los investigadores desean conocer si la preferencia por el café negro está relacionada con el género de la persona, y especificar la respuesta con un nivel de significancia de α = 0.05.

Para ello se dispone de una muestra de 100 personas entrevistadas y sus respuestas:

Paso 1

Establecer las hipótesis:

-H_o: el género y la preferencia por el café negro son independientes.
-H₁: el gusto por el café negro está relacionado con el género de la persona.

Paso 2

Calcular las frecuencias esperadas para la distribución, para lo cual se requieren los totales añadidos en la última fila y en la columna de la derecha de la tabla. Cada celda en el recuadro rojo tiene un valor esperado f_e, que se calcula multiplicando el total de su fila F por el total de su columna C, dividido por el total de la muestra N:

f_e = (F x C) /N

Los resultados son los siguientes para cada celda:

-C1: (36 x 47) / 100 = 16.92
-C2: (64 x 47) / 100 = 30.08
-C3: (36 x 53) / 100 = 19.08
-C4: (64 x 53) / 100 = 33.92

Paso 3

Seguidamente hay que calcular el estadístico chi cuadrado para esta distribución, de acuerdo a la fórmula dada:

Paso 4

Determinar χ²_crítico, sabiendo que los datos registrados están en f = 2 filas y c = 2 columnas, por lo tanto, el número de grados de libertad es:

k = (2-1)⋅(2-1) = 1.

Lo cual significa que debemos buscar en la tabla mostrada arriba el valor de χ²_{k, α} = χ²_{1; 0.05}, el cual es:

χ²_crítico = 3.841

Paso 5

Comparar los valores y decidir:

χ² = 2.9005