Diferencia entre una fracción común y un número decimal
Para identificar qué diferencia hay entre una fracción común y un número decimal basta con observar ambos elementos: uno representa un número racional, y el otro incluye en su constitución una parte entera y otra decimal.
Una “fracción común” es la expresión de una cantidad dividida entre otra, sin efectuar dicha división. Matemáticamente, una fracción común es un número racional, el cual se define como el cociente de dos números enteros “a/b”, donde b≠0.

Un “número decimal” es un número que consta de dos partes: una parte entera y una parte decimal.
Para separar la parte entera de la parte decimal se coloca una coma, llamada coma decimal, aunque dependiendo la bibliografía también se utiliza un punto.
Números decimales
Un número decimal puede tener una cantidad finita o infinita de números en su parte decimal. Además, la cantidad infinita de decimales se puede descomponer en dos tipos:
Periódica
Es decir, que posee un patrón de repetición. Por ejemplo, 2,454545454545…
No periódica
No tienen ningún patrón de repetición. Por ejemplo, 1,7845265397219…
A los números que poseen una cantidad finita o infinita periódica de decimales se les llama número racionales, mientras que a los que poseen una cantidad infinita no periódica se les llama irracionales.
La unión del conjunto de los números racionales y el conjunto de los número irracionales es conocido como el conjunto de los números reales.

Diferencias entre fracción común y número decimal
Las diferencias entre una fracción común y un número decimal son:
1- Parte decimal
Toda fracción común posee una cantidad finita de números en su parte decimal o una cantidad infinita periódica, mientras que un número decimal puede tener una cantidad infinita no periódica de números en su parte decimal.
Lo anterior dice que todo número racional (toda fracción común) es un número decimal, pero no todo número decimal es un número racional (una fracción común).
2- Notación
Toda fracción común es denotada como el cociente de dos números enteros, mientras que un número decimal irracional no se puede denotar de esta manera.
Los números decimales irracionales más usados en las matemáticas son denotados por raíces cuadradas (√ ), cúbicas (³√ ) y de grados superiores.
Además de estos, están dos números muy famosos, que son el número de Euler, denotado por e; y el número pi, denotado por π.

¿Cómo pasar de una fracción común a un número decimal?
Para pasar de una fracción común a un número decimal solo basta efectuar la división correspondiente. Por ejemplo, si se tiene 3/4, el número decimal correspondiente es 0,75.
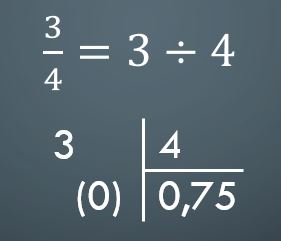
¿Cómo pasar de un número decimal racional a una fracción común?
El proceso inverso al anterior también se puede realizar. El siguiente ejemplo ilustra una técnica para pasar de un número decimal racional a una fracción común:
– Sea x=1,78
Como x tiene dos decimales, entonces se multiplica la igualdad anterior por 10²=100, con lo cual se obtiene que 100x=178; y despejando x resulta que x=178/100. Esta última expresión es la fracción común que representa al número 1,78.
Pero, ¿se puede realizar este proceso para números con una cantidad infinita periódica de decimales? La respuesta es sí, y el siguiente ejemplo muestra los pasos a seguir:
– Sea x=2,193193193193…
Como el período de este número decimal tiene 3 dígitos (193) entonces se multiplica la expresión anterior por 10³=1000, con lo cual se obtiene la expresión 1000x=2193,193193193193….
Ahora se resta la última expresión con la primera y toda la parte decimal se anula, quedando la expresión 999x=2191, de donde se obtiene que la fracción común es x=2191/999.
