Dominio y contradominio de una función (con ejemplos)

Los conceptos de dominio y contradominio de una función son enseñados comúnmente en los cursos de cálculo que se imparten al comienzo de las carreras universitarias.

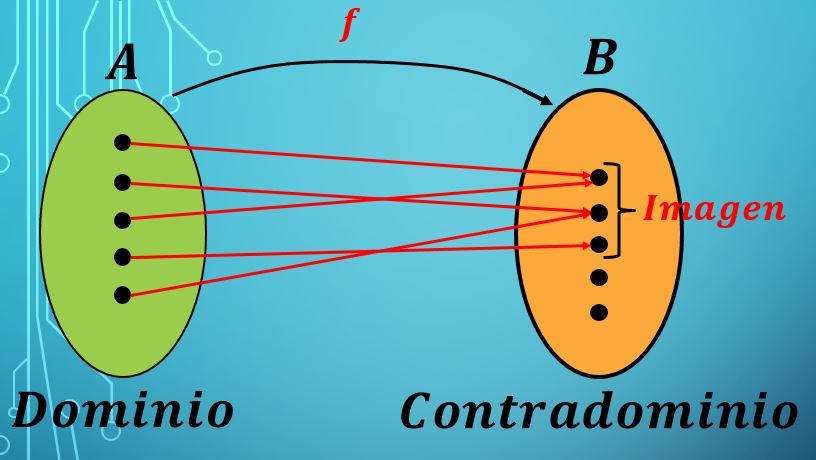
Antes de definir el dominio y el contradominio se debe saber qué es una función. Una función f es una ley (regla) de correspondencia hecha entre los elementos de dos conjuntos.

Al conjunto del cual se escogen los elementos se le llama dominio de la función, y al conjunto al cual son enviados estos elementos a través de f se le llama contradominio.

En matemáticas una función con dominio A y contradominio B es denotada por la expresión f : A → B.

La expresión anterior dice que los elementos del conjunto A son enviados al conjunto B siguiendo la ley de correspondencia f.

Una función asigna a cada elemento del conjunto A un único elemento del conjunto B.

Dominio y contradominio

Dada una función real de una variable real f(x), se tiene que el dominio de la función serán todos aquellos números reales tales que, cuando se evalúan en f, el resultado es un número real.

Generalmente, el contradominio de una función es el conjunto de los números reales R. Al contradominio también se le llama conjunto de llegada o codominio de la función f.

¿El contradominio de una función siempre es R?

No. Mientras no se estudie en detalle la función, se suele tomar como contradominio el conjunto de los números reales R.

Pero una vez estudiada la función, se puede tomar un conjunto más adecuado como contradominio, el cual será un subconjunto de R.

El conjunto adecuado que se mencionó en el párrafo anterior coincide con la imagen de la función.

La definición de la imagen o rango de una función f hace referencia a todos los valores que provienen de evaluar un elemento del dominio en f.

Ejemplos de dominio y contradominio

En los siguientes ejemplos se ilustra cómo calcular el dominio de una función y su imagen.

Ejemplo 1

Sea f una función real definida por f(x)=2.

El dominio de f son todos los números reales tales que, al evaluarlos en f, el resultado es un número real. El contradominio por el momento es igual a R.

Como la función dada es constante (siempre igual a 2), se tiene que no importa qué número real se escoja, ya que al evaluarlo en f el resultado siempre será igual a 2, el cual es un número real.

Por lo tanto, el dominio de la función dada son todos los números reales; es decir, A=R.

Ahora que ya es sabido que el resultado de la función siempre es igual a 2, se tiene que la imagen de la función es solo el número 2, por lo tanto el contradominio de la función puede ser redefinido como B=Img(f)={2}.

Por lo tanto, f : R → {2}.

Ejemplo 2

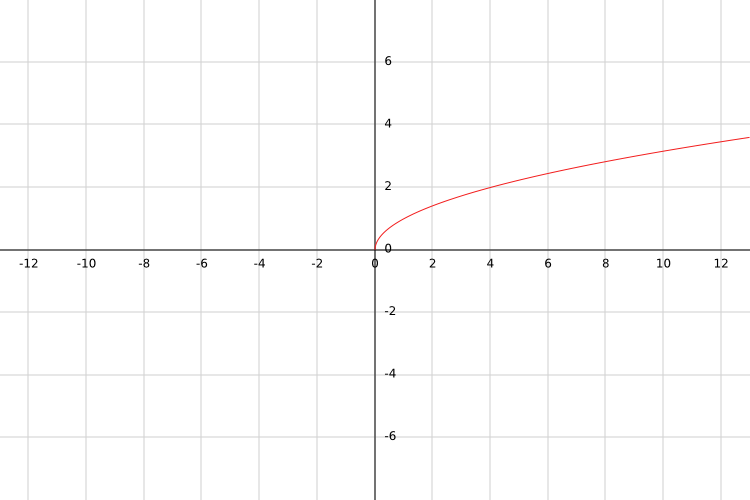
Sea g una función real definida por g(x)=√x.

Mientras no se conozca la imagen de g, el contradominio de g es B=R.

Con esta función se debe tener tomar en cuenta que las raíces cuadradas solo están definidas para números no negativos; es decir, para números mayores o iguales que cero. Por ejemplo, √-1 no es un número real.

Por lo tanto, el dominio de la función g deben ser todos los números mayores o iguales que cero; esto es, x ≥ 0.

Por lo tanto, A=[0,+∞).

Para calcular el rango se debe notar que cualquier resultado de g(x), por ser una raíz cuadrada, siempre será mayor o igual que cero. Es decir, B=[0,+∞).

En conclusión, g : [0,+∞)→[0,+∞).

Ejemplo 3

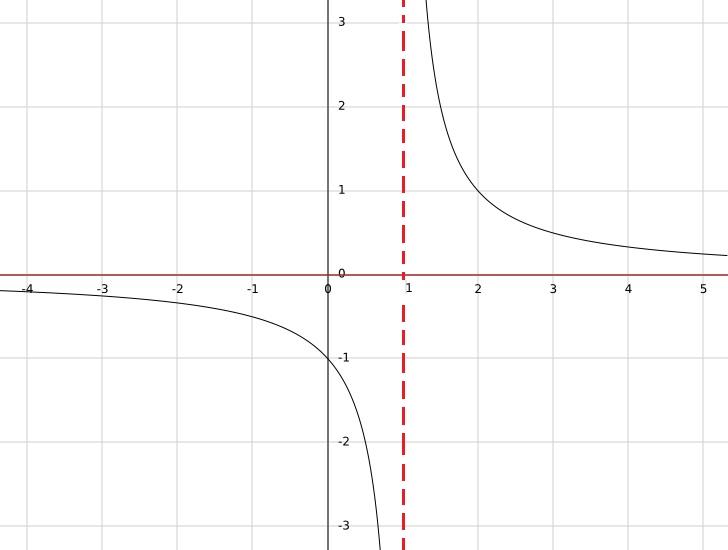
Si se tiene la función h(x)=1/(x-1), se tiene que esta función no está definida para x=1, puesto que en el denominador se obtendría cero y la división por cero no está definida.

Por otro lado, para cualquier otro valor real el resultado será un número real. Por lo tanto, el dominio son todos los reales excepto el uno; es decir, A=R/{1}.

Del mismo modo se puede observar que el único valor que no puede obtenerse como resultado es el 0, puesto que para que una fracción sea igual a cero el numerador debe ser cero.

Por lo tanto, la imagen de la función es el conjunto de todos los reales excepto el cero, entonces se toma como contradominio B=R/{0}.

En conclusión, h : R/{1}→R/{0}.

Observaciones

El dominio y la imagen no tienen que ser el mismo conjunto, como se demostró en los ejemplos 1 y 3.

Cuando se grafica una función en el plano cartesiano, el dominio es representado por el eje X y el contradominio o el rango es representado por el eje Y.