Área de un pentágono regular e irregular: cómo se saca, ejercicios
Para calcular el área de un pentágono primero necesitamos determinar si este es regular o no lo es. Un pentágono es un polígono, una figura plana cerrada de cinco lados. Cuando un polígono es regular, significa que la longitud de sus lados es la misma y sus ángulos internos también.
En ese caso, existe una fórmula para calcular el área exacta del polígono regular, conociendo algunas de sus características principales, la cual deduciremos más adelante.
Si el polígono no es regular, es decir, tiene lados de distintos tamaños, y ángulos internos desiguales, no existe una fórmula única.
Sin embargo, los matemáticos han encontrado estrategias de cálculo, como por ejemplo dividir la figura en otras con menor número de lados, como triángulos, cuadrados y rectángulos, cuyas dimensiones se conozcan o calculen con facilidad.
Otro procedimiento para calcular áreas de polígonos en general, conociendo las coordenadas de sus vértices, es el método llamado determinantes de Gauss, que describiremos más adelante.
Índice del artículo
- 1 ¿Cómo calcular el área de un pentágono regular?
- 2 ¿Cómo calcular el área de un pentágono irregular?
- 3 Ejercicios resueltos
- 4 Referencias
Vamos a tomar un pentágono regular de lado a, y lo vamos a dividir en 5 triángulos iguales como se muestra en la figura, trazando segmentos desde el centro (rojo) hasta los vértices (azul).
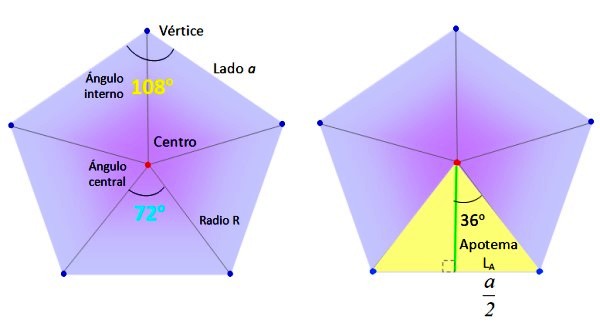
A su vez los triángulos, como el destacado en color amarillo a la derecha en la figura superior, se dividen en dos triángulos rectángulos iguales, gracias al segmento verde, llamado apotema.
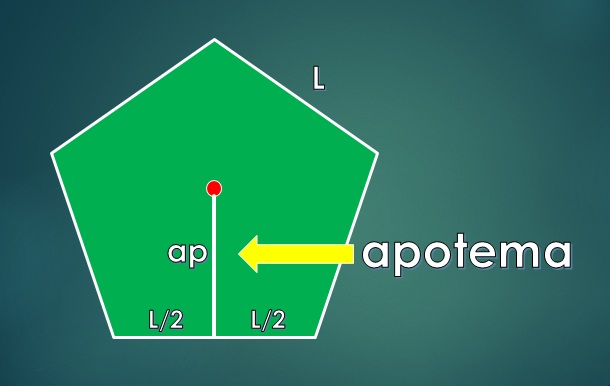
La apotema se define como el segmento perpendicular que conecta al centro del polígono con el centro de uno de los lados. Su longitud es LA.
El área de un triángulo rectángulo de base a/2 y altura LA es:
[(a/2) x LA]
El pentágono tiene 10 triángulos como este, por lo tanto su área es:
A = 10 (a/2) x LA
Pero el perímetro P del pentágono es precisamente P =10a, por lo tanto el área viene dada por el semiproducto del perímetro y la longitud de la apotema:
A = P x LA /2
Expresando la longitud de la apotema LA en función del lado a, sabiendo que el ángulo indicado es la mitad del ángulo central, es decir 36º, equivalente a:
36º = π/5
Por trigonometría elemental, mediante la tangente del ángulo agudo 36º:
tan (π/5) = (a/2) ÷ LA
De allí que:
LA= (a/2) ÷ tan (π/5)
Sustituyendo en el área deducida en el apartado anterior, y sabiendo que P = 5a:
A = P x LA /2

El radio de un polígono regular es el segmento que va desde el centro hasta uno de sus vértices. Coincide con el radio de la circunferencia circunscrita, como se muestra en la siguiente figura:
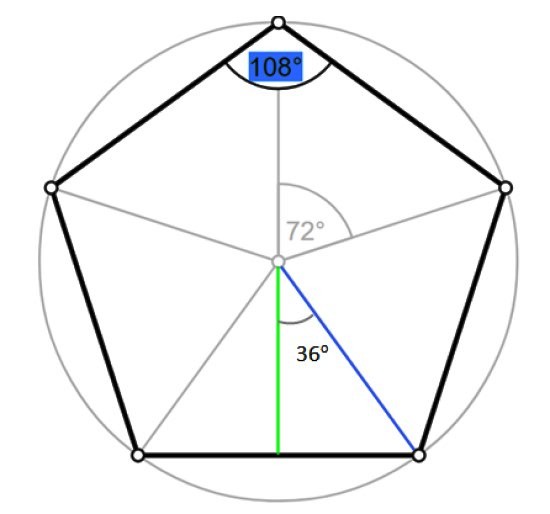
Sea R la medida de dicho radio, que coincide con la hipotenusa del triángulo rectángulo delineado en la figura anterior, en color azul. Por trigonometría:
cos 36º = cos (π/5) = LA ÷ R
Y
sen 36º = sen (π/5) = (a/2) ÷ R
Por lo tanto:
A = P x LA /2 = 5R. sen (π/5) x R. cos (π/5) = 5R2 [sen (π/5) x cos (π/5)]
Utilizando la fórmula del ángulo doble:
sen (2θ) = 2 sen θ . cos θ
Nos queda que:
[sen (π/5) x cos (π/5)] = (1/2) sen 72º
Y así, por sustitución de este valor, obtenemos la siguiente fórmula para el área del pentágono regular:
A = (5/2)R2.sen 72º
Como hemos dicho con anterioridad, para un polígono irregular no hay una fórmula única, pero hay dos métodos que suelen funcionar muy bien, el primero se llama triangulación y el segundo es el método de los determinantes de Gauss.
Consiste en dividir la figura en triángulos, cuya área es más fácil de calcular, o también se puede probar con otras figuras cuya área se conozca, como cuadrados, rectángulos y trapecios.
Otra forma de hallar el área del pentágono irregular u otro polígono irregular, es colocando la figura en un sistema de coordenadas cartesianas, con la finalidad de hallar las coordenadas de los vértices.
Conocidas estas coordenadas, se aplica el método de determinantes de Gauss para calcular el área, el cual viene dado por la siguiente fórmula:
Donde A es el área del polígono y (xn , yn ) son las coordenadas de los vértices. Un polígono de n lados tiene 5 vértices, para el pentágono sería n= 5:
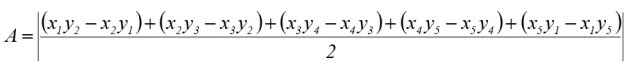
Las barras que acompañan la fórmula son las barras de módulo o valor absoluto.
Esto significa que aunque el resultado de la operación sea negativo, deberemos expresarlo con signo positivo, y si ya es positivo, pues hay que dejarlo con ese signo. Ello se debe a que un área siempre es una cantidad positiva.
El procedimiento recibe el nombre de determinantes de Gauss por su creador, el matemático alemán Carl F. Gauss (1777-1855). Las operaciones indicadas equivalen al determinante de una matriz de 2×2, por ejemplo el primer determinante es:
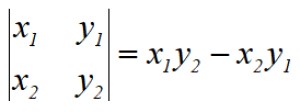
Para hallar el área del pentágono debemos resolver 5 determinantes, sumar el resultado algebraicamente, dividirlo por 2 y finalmente expresar el área siempre con signo positivo.
Encontrar el área del pentágono regular cuya apotema vale 4 cm y cuyo lado mide 5.9 cm.
Solución
Ya que se trata de un pentágono regular, y tenemos la medida del lado y de la apotema, empleamos la fórmula deducida anteriormente:
A = P x LA /2
El perímetro P es igual a 5a = 5 x 5.9 cm = 29.5 cm.
A = 29.5 cm x 4 cm / 2 = 59 cm2
Hallar el área del pentágono irregular mostrado. Se conocen las siguientes dimensiones:
DC ≈ DE
AE=AB=5
BC=12
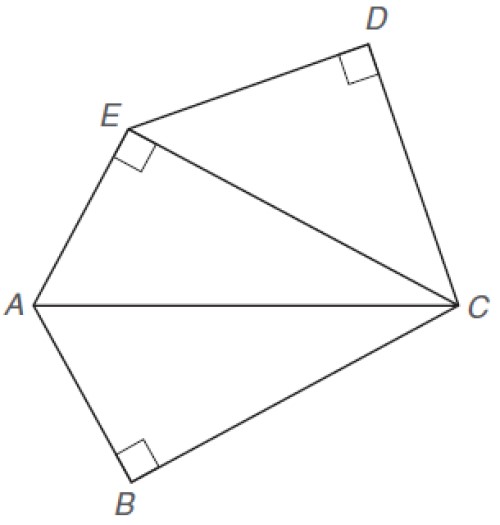
Solución
El área del pentágono es la suma de las áreas de los triángulos, los cuales son rectángulos. El enunciado dice que DC ≈ DE, por lo tanto al aplicar el teorema de Pitágoras al triángulo EDC se tiene:
EC2 = 2 ED2. Entonces EC = √2.ED.
Los triángulos AEC y ABC tienen hipotenusa común, que es el segmento AC, por lo tanto:
EA2 + EC2 = AB2 + BC2
Como EA y AB miden lo mismo, se obtiene que:
EC = BC = √2.ED
Ya que BC = 12, entonces ED = 12 / √2= 8.485.
Con estos valores calcularemos el área de cada triángulo y las sumaremos al final.
Área del triángulo EDC
ED x DC /2 = 8.4852 / 2 = 36
Área del triángulo AEC
EA x EC / 2 = EA x √2.ED / 2 = 5 x √2. 8.485 / 2 = 30
Área del triángulo ABC
AB x BC / 2
Luego el área buscada es:
5 x 12/2 = 30
Es la misma que la del triángulo AEC, puesto que ambos tienen las mismas medidas.
Área del pentágono irregular
Finalmente el área solicitada es la suma de las áreas de los tres triángulos:
A = 36 + 30 + 30 unidades = 96 unidades.
- Alexander, D. 2013. Geometría. 5ta. Edición. Cengage Learning.
- Math Open Reference. Area of a polygon. Recuperado de: mathopenref.com.
- Universo Fórmulas. Área de un pentágono irregular. Recuperado de: universoformulas.com.
- Universo Fórmulas. Área de un pentágono regular. Recuperado de: universoformulas.com.
- Wikipedia. Pentágono. Recuperado de: es.wikipedia.com.
