Velocidad relativa: concepto, ejemplos, ejercicios
La velocidad relativa de un objeto es aquella que se mide respecto a un observador dado, ya que otro observador puede obtener una medida diferente. La velocidad siempre depende del observador que la mida.
Por ello la velocidad de un objeto medida por cierta persona, será la velocidad relativa respecto de ella. Otro observador puede obtener un valor distinto para la velocidad, aún tratándose del mismo objeto.
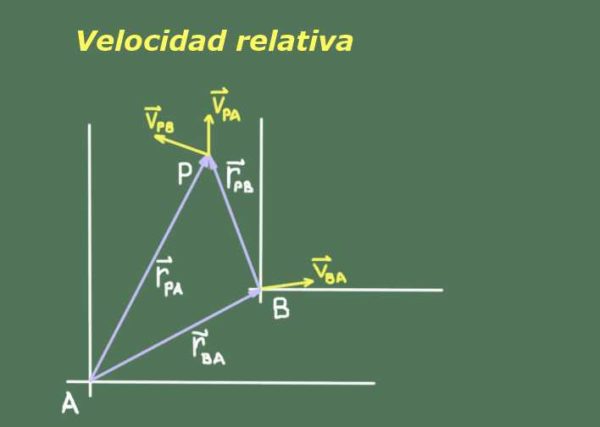
Como dos observadores A y B que se mueven entre sí pueden tener medidas diferentes de un tercer objeto P que se mueve, es necesario buscar una relación entre las posiciones y velocidades de P vistas por A y B.
La figura 1 muestra dos observadores A y B con sus respectivos sistemas de referencia, desde el cuál miden la posición y la velocidad del objeto P.
Cada observador A y B mide la posición y la velocidad del objeto P en un determinado instante de tiempo t. En la relatividad clásica (o galileana) el tiempo para el observador A es el mismo que para el observador B independientemente de sus velocidades relativas.
Este artículo trata sobre relatividad clásica que es válida y aplicable a la mayoría de las situaciones cotidianas en la que los objetos tienen velocidades mucho menores que la de la luz.
La posición del observador B respecto de A la denotamos como rBA. Como la posición es una cantidad vectorial usamos negritas para indicarlo. La posición del objeto P respecto de A se denota como rPA y la del mismo objeto P respecto de B rPB.
Índice del artículo
- 1 Relación entre posiciones y velocidades relativas
- 2 Velocidad relativa entre la moto y el coche
- 3 Referencias
Hay una relación vectorial entre estas tres posiciones que puede deducirse a partir de la representación de la figura 1:
rPA= rPB + rBA
Si se toma la derivada de la expresión anterior con respecto al tiempo t obtendremos la relación entre las velocidades relativas de cada observador:
VPA= VPB + VBA
En la expresión anterior se tiene la velocidad relativa de P respecto de A en función de la velocidad relativa de P respecto de B y de la velocidad relativa de B respecto de A.
Similarmente puede escribirse la velocidad relativa de P respecto de B en función de la velocidad relativa de P respecto de A y de la velocidad relativa de A respecto de B.
VPB= VPA + VAB
Debe notarse que la velocidad relativa de A respecto de B es igual y contraria a la de B respecto de A:
VAB = –VBA
Un coche va por una carretera recta, que va de oeste a este, con rapidez de 80 km/h mientras que en la dirección contraria (y por el otro carril) viene una moto con rapidez de 100 km/h.
En el asiento trasero del coche viaja un niño que desea conocer la velocidad relativa de una moto que se acerca a él. Para averiguar la respuesta, el niño aplicará las relaciones que acaba de leer en el apartado anterior, identificando cada sistema de coordenadas de la siguiente manera:
-A es el sistema de coordenadas de un observador en la carretera y respecto de él se han medido las rapideces de cada vehículo.
-B es el coche y P será la moto.
Si se quiere calcular la velocidad de la moto P respecto de el coche B se aplicará la siguiente relación:
VPB= VPA + VAB=VPA – VBA
Tomando como positiva la dirección oeste-este se tiene:
VPB= (-100 km/h – 80 km/h) i = -180 km/h i
Este resultado se interpreta así: la moto se mueve respecto del coche con una rapidez de 180 km/h y dirección –i, es decir de este a oeste.
La moto y el coche se han cruzado siguiendo cada cual su carril. El niño que va en el asiento trasero del coche ve alejarse la moto y ahora quiere saber a qué velocidad se aleja respecto de él, suponiendo que ambos, moto y coche mantienen las mismas rapideces que antes de cruzarse.
Para conocer la respuesta el niño aplica la misma relación que se usó anteriormente:
VPB= VPA + VAB=V PA – VBA
VPB= -100 km/h i – 80 km/h i = -180 km/h i
Y ahora la moto se aleja del coche con la misma rapidez relativa con la que se acercaba antes que se cruzasen.
La misma moto del parte 2 se regresa manteniendo su misma rapidez de 100 km/h pero cambiando su dirección. Es decir el coche (que continúa con rapidez 80 km/h) y la moto se mueven ambos en dirección positiva este-oeste.
En un momento dado la moto rebasa al coche, y el niño que va en el asiento trasero del coche desea saber la velocidad relativa de la moto respecto de él cuando la ve pasar a su lado.
Para obtener la respuesta el niño aplica nuevamente las relaciones del movimiento relativo:
VPB= VPA + VAB=VPA – VBA
VPB= +100 km/h i – 80 km/h i = 20 km/h i
El niño desde el asiento trasero observa a la moto adelantando al coche con una rapidez de 20 km/h.
Ejercicio 1
Un bote a motor cruza un río de 600 m de ancho y que fluye de norte a sur. La rapidez del río es de 3 m/s. La velocidad del bote respecto al agua del río es de 4 m/s hacia el este.
(i) Halle la velocidad del bote respecto a la orilla del río.
(ii) Indique la rapidez y dirección del bote respecto a tierra.
(iii) Calcule el tiempo de cruce.
(iv) Cuánto se habrá desplazado hacia el sur respecto al punto de partida.
Solución
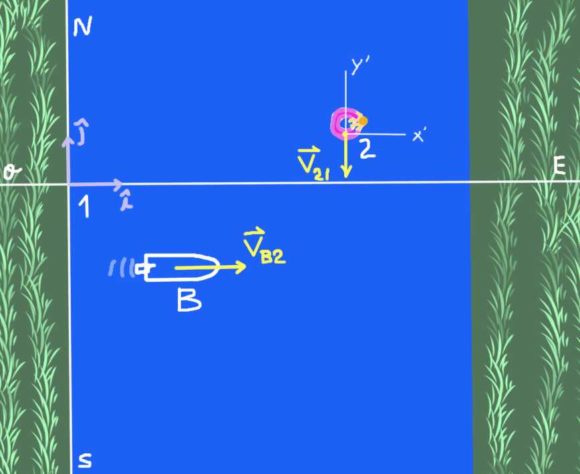
Hay dos sistemas de referencia: el sistema de referencia solidario a la orilla del río que llamaremos 1 y el sistema de referencia 2 que es un observador que flota sobre el agua del río. El objeto de estudio es el bote B.
La velocidad del bote respecto al río se escribe en forma vectorial de la siguiente manera:
VB2 = 4 i m/s
La velocidad del observador 2 (balsa sobre el río) respecto al observador 1 (en tierra):
V21 = -3 j m/s
Se desea encontrar la velocidad del bote respecto a tierra VB1.
VB1 = VB2 + V21
Respuesta i
VB1 = (4 i – 3 j) m/s
La rapidez del bote será el módulo de la velocidad anterior:
|VB1| = ( 42 + (-3)2 )½ = 5 m/s
Respuesta ii
Y la dirección será:
θ= arctan( -¾ ) = -36,87º
Respuesta iii
El tiempo de cruce del bote es el cociente entre el ancho del río y la componente x de la velocidad del bote respecto a tierra.
t= (600m)/(4 m/s) = 150 s
Respuesta iv
Para calcular la deriva que tuvo el bote hacia el sur se multiplica la componente y de la velocidad del bote respecto a tierra por el tiempo de cruce:
d = -3 j m/s * 150 s = -450 j m
El desplazamiento hacia el sur respecto del punto de partida es de 450m.
- Giancoli, D. Physics. Principles with Applications. 6th Edition. Prentice Hall. 80-90
- Resnick, R. (1999). Física. Volumen 1. Tercera edición en español. México. Compañía Editorial Continental S.A. de C.V. 100- 120.
- Serway, R., Jewett, J. (2008). Física para Ciencias e Ingeniería. Volumen 1. 7ma. Edición. México. Cengage Learning Editores. 95-100.
- Wikipedia. Velocidad relativa. Recuperado de: wikipedia.com
- Wikipedia. Método de la velocidad relativa. Recuperado de: wikipedia.com
