Polígonos regulares: propiedades, elementos, ángulos, ejemplos
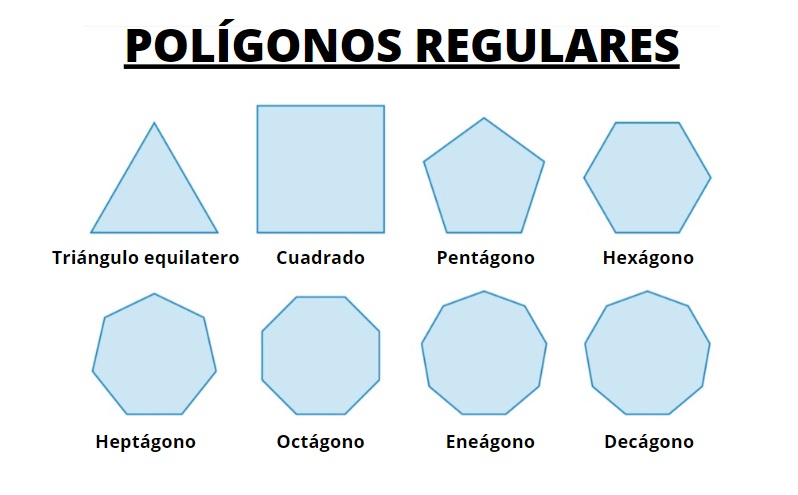
Los polígonos regulares son aquellos que tienen todos sus lados y sus ángulos internos iguales. En la siguiente figura hay un conjunto de distintos polígonos, que son figuras planas limitadas por una curva cerrada y solamente los que están resaltados cumplen con las condiciones para ser regulares.
Por ejemplo el triángulo equilátero es un polígono regular, ya que sus tres lados miden lo mismo, así como sus ángulos internos, que valen 60 º cada uno.
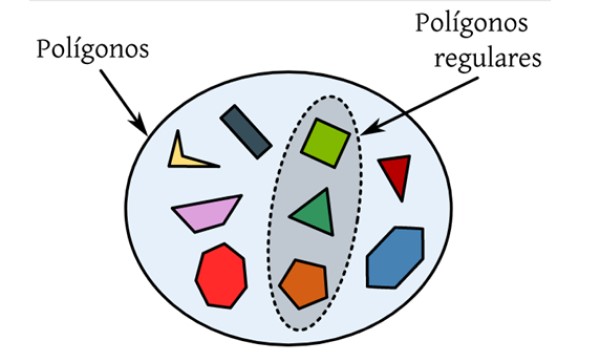
El cuadrado es un cuadrilátero con cuatro lados de igual medida y cuyos ángulos internos son de 90º. Le sigue el pentágono regular, con cinco lados de igual tamaño y cinco ángulos internos de 108º cada uno.
Cuando un polígono es regular, se le añade dicha palabra a su nombre especial, así tenemos el hexágono regular, el heptágono regular y así sucesivamente.
Índice del artículo
- 1 Propiedades de los polígonos regulares
- 2 Elementos de un polígono regular
- 3 Perímetro y área
- 4 Ángulos
- 5 Ejemplos de polígonos regulares
- 6 Ejercicio resuelto
- 7 Referencias
Las propiedades más importantes de los polígonos regulares pueden resumirse como sigue:
-Los lados miden igual, por lo tanto son equiláteros.
-Son equiangulares, pues todos sus ángulos internos tienen igual medida.
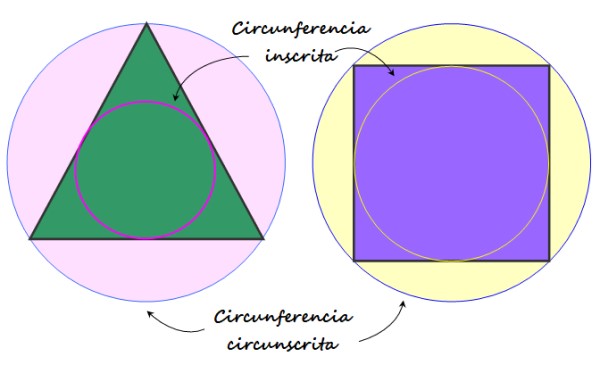
-Siempre se pueden inscribir en una circunferencia, lo que quiere decir que encajan perfectamente dentro de una, la cual se denomina circunferencia circunscrita.
-Para un polígono regular de n lados, la medida de un ángulo interior α es:
α = [180 (n-2)]/n
-Se pueden trazar n(n-3)/2 diagonales desde los vértices de un polígono, ya sea regular o no.
-La suma de los ángulos exteriores es igual a 360º.
Seguidamente presentamos los elementos principales de un polígono regular, visualizados en la figura inferior.
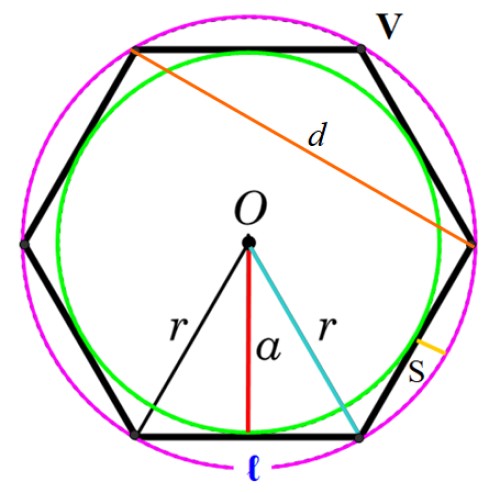
Punto en común que tienen dos lados consecutivos, denotado como V en la figura.
Es el segmento que une dos vértices consecutivos del polígono y se denota como ℓ o L.
Segmento que une dos vértices no consecutivos del polígono, en la figura se denota como d.
Es el centro común de la circunferencia inscrita y la circunferencia circunscrita, denotado por la letra O. También se puede ver como el único punto que equidista tanto de los vértices como de los puntos medios de cada lado.
Es el radio r de la circunferencia circunscrita y coincide con la distancia entre O y un vértice.
Se denomina apotema al radio de la circunferencia inscrita en el polígono, representado en la figura con una letra a. El apotema es perpendicular a un lado y une a este con el centro O (segmento rojo en la figura 3).
Conociendo el radio r y la longitud del lado, la apotema se calcula mediante:
Ya que, en efecto, el apotema es uno de los catetos de un triángulo rectángulo (ver figura 3), siendo el otro cateto el valor de ℓ/2 (la mitad de un lado) y la hipotenusa el radio r del polígono.
Cuando se aplica el teorema de Pitágoras a dicho triángulo, se obtiene esta ecuación, que es válida no solamente para el hexágono, sino para cualquier polígono regular.
Es el ángulo cuyo vértice coincide con el centro O y cuyos lados son los segmentos que unen al centro con dos vértices consecutivos. Su medida en grados sexagesimales es 360º/n, donde n es el número de lados del polígono.
Es la diferencia entre el radio del polígono y la apotema (ver figura 3). Denotando la sagita como S:
S = r – a
Se calcula fácilmente sumando las longitudes de los lados. Como cualquier lado tiene igual longitud L y hay n lados, el perímetro P se expresa como:
P = n.L
En un polígono regular el área A viene dada por el producto entre el semi-perímetro (la mitad del perímetro) y la longitud del apotema a.
A = P.a /2
Como el perímetro depende del número de lados n, resulta que:
A = (nL).a /2
Dos polígonos regulares pueden tener el mismo perímetro aunque no tengan el mismo número de lados, ya que dependería entonces de la longitud de los lados.
En el libro V de su Colección, el matemático Pappus de Alejandría (290-350), último de los grandes matemáticos griegos de la antigüedad, demostró que entre todos los polígonos regulares con el mismo perímetro, el de mayor área es el que tiene un mayor número de lados.
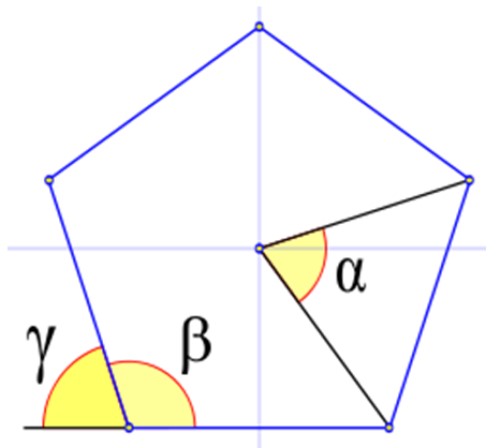
En la figura 4 se muestran los ángulos relevantes en un polígono regular, denotados con las letras griegas α, β y γ.
Con anterioridad mencionamos al ángulo central, entre los elementos del polígono regular, se trata del ángulo cuyo vértice está en el centro del polígono y los lados son los segmentos que unen al centro con dos vértices consecutivos.
Para calcular la medida del ángulo central α, se divide 360º entre n, el número de lados. O bien 2π radianes entre n:
α = 360º/n
Equivalente en radianes a:
α = 2π /n
En la figura 4 el ángulo interno β es aquel cuyo vértice coincide con uno de la figura y sus lados son lados de la figura también. Se calcula en grados sexagesimales mediante:
β = [180 (n-2)]/n
O en radianes usando:
β = [π (n-2)]/n
Se denotan mediante la letra griega γ. En la figura se observa que γ + β = 180º. Por lo tanto:
γ = 180º – β
La suma de todos los ángulos externos a un polígono regular es 360º.
A continuación tenemos los primeros 8 polígonos regulares. Observamos que a medida que aumenta el número de lados, el polígono se asemeja cada vez más a la circunferencia en la cual están inscritos.
Podemos imaginar que haciendo la longitud de los lados cada vez más pequeña, y aumentando el número de estos, conseguimos la circunferencia.
Los polígonos regulares se encuentran por doquier en la vida diaria y hasta en la naturaleza. Veamos algunos ejemplos:
Señales de tráfico
En la señalización que vemos en autopistas y carreteras abundan los polígonos regulares como triángulos equiláteros, cuadrados y rombos. En la figura 6 vemos una señal de alto con forma octogonal.

Mobiliario
Innumerables piezas de mobiliario tienen al cuadrado por ejemplo, como figura geométrica característica, así como muchas mesas, sillas y bancos son cuadrados. Un paralelepípedo es generalmente una caja con lados en forma de rectángulo (que no es un polígono regular), pero también pueden hacerse cuadrados.
Arquitectura y construcción
Las teselas o baldosas de los pisos y paredes, tanto en hogares como en las calles, con frecuencia tienen forma de polígonos regulares.
Los teselados son superficies cubiertas enteramente con teselas que tienen figuras geométricas diversas. Con el triángulo, el cuadrado y el hexágono se pueden hacer teselados regulares, aquellos que emplean únicamente un solo tipo de figura para recubrir perfectamente, sin que queden espacios vacíos (ver figura 6).
Asimismo las edificaciones hacen uso de los polígonos regulares en elementos como ventanas y decoración.

Sorprendentemente, el hexágono regular es un polígono que aparece con frecuencia en la naturaleza.
Los panales hechos por las abejas para almacenar la miel tienen una forma muy aproximada a un hexágono regular. Tal como observó Pappus de Alejandría, de esta manera las abejas optimizan el espacio para guardar la mayor cantidad posible de miel.
Y también hay hexágonos regulares en el caparazón de las tortugas y los copos de nieve, que adoptan también diversas formas geométricas muy hermosas.
Un hexágono regular se inscribe en una semicircunferencia de 6 cm de radio, tal como se muestra en la figura. ¿Cuál es el valor del área sombreada?
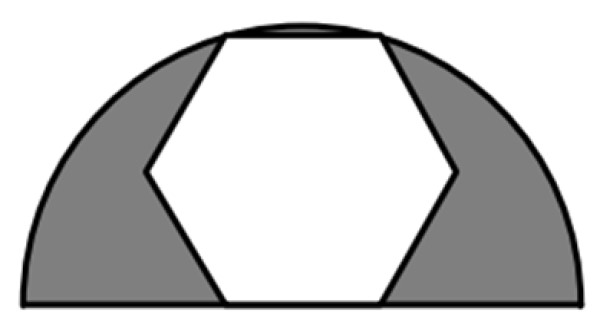
El área sombreada es la diferencia entre el área del semicírculo de radio R = 6 cm y el área del hexágono completo, un polígono regular de 6 lados. Así que necesitaremos de fórmulas para el área de cada de una de estas figuras.
Área del semicírculo
A1 = π R2 /2 = π (6 cm)2 /2= 18π cm2
Área del hexágono regular
La fórmula para calcular el área de un polígono regular es:
A = P.a /2
Donde P es el perímetro y a es el apotema. Como el perímetro es la suma de los lados, necesitaremos el valor de estos. Para el hexágono regular:
P = 6ℓ
Por lo tanto:
A = 6ℓa /2
Para hallar el valor del lado ℓ es preciso construir figuras auxiliares, que explicaremos seguidamente:
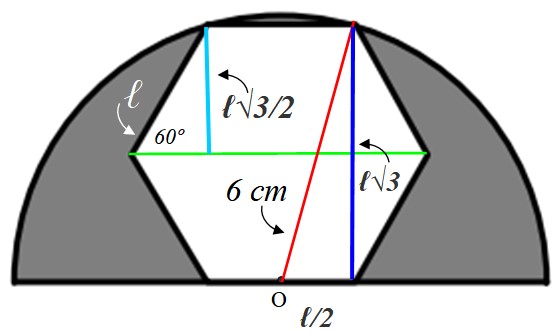
Comencemos por el triángulo rectángulo pequeño a la izquierda, cuya hipotenusa es ℓ. Un ángulo interno del hexágono vale:
α = [180 (n-2)]/n = α = [180 (6-2)]/6 = 120º
El radio que hemos trazado en color verde bisecta este ángulo, por lo tanto el ángulo agudo del triángulo pequeño es de 60º. Con la información suministrada se resuelve dicho triángulo, encontrando el lado azul claro, que mide lo mismo que el apotema:
Cateto opuesto = a = ℓ x sen 60º = ℓ√3 / 2 cm
Este valor es el doble del cateto azul oscuro del triángulo grande a la derecha, pero de ese triángulo sabemos que la hipotenusa mide 6 cm por ser el radio de la semicircunferencia. El cateto restante (abajo) vale ℓ/2 ya que el punto O se encuentra en medio del lado.
Dado que no se conocen ángulos internos de este triángulo, podemos plantear el teorema de Pitágoras para él:
36 = 3 ℓ2 + ℓ2 / 4
(13/4) ℓ2 = 36 → ℓ = √(4 x36)/13 cm = 12 /√13 cm
Con este valor se calcula el apotema:
a = ℓ√3 / 2 cm = (12 /√13) x (√3 /2) cm = 6√3/√13 cm
Llamemos A2 al área del hexágono regular:
= 28. 8 cm2
Área de la figura sombreada
A1 – A2 = 18π cm2 – 28.8 cm2 = 27.7 cm2
- Baldor, A. 1973. Geometría y trigonometría. Editorial Cultural Centroamericana.
- Disfruta las matemáticas. Teselaciones. Recuperado de: disfrutalasmatematicas.com.
- E. A. 2003. Elementos de geometría: con ejercicios y geometría del compás. Universidad De Medellín.
- Hexágonos en la naturaleza. Recuperado de: malvargamath.wordpress.com.
- Jiménez, R. 2010. Matemáticas II. Geometría y Trigonometría. Segunda edición. Prentice Hall.
- Polígonos regulares. Recuperado de: mate.ingenieria.usac.edu.gt.
- Wikipedia. Apotema. Recuperado de: es.wikipedia.org.
