Ángulos opuestos por el vértice (con ejercicio resuelto)
Los ángulos opuestos por el vértice son los que cumplen lo siguiente: los lados de uno de ellos son las prolongaciones de los lados del otro ángulo. El teorema fundamental de los ángulos opuestos por el vértice dice así: dos ángulos opuestos por el vértice tienen la misma medida.
Muchas veces se abusa del lenguaje diciendo que los ángulos opuestos por el vértice son iguales, lo cual no es correcto. El hecho que dos ángulos tengan la misma medida no significa que sean iguales. Es como decir que dos niños que tengan la misma altura son iguales.
Recordemos que un ángulo se define como la figura geométrica compuesta por dos semirrectas con el mismo origen.
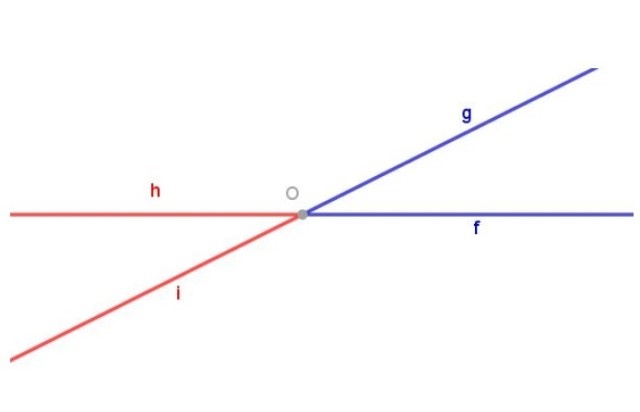
En la figura 1 se muestra el ángulo fOg (azul) compuesto por la semirrecta [Of) y la semirrecta [Og) de origen común O. La figura 1 también muestra el ángulo hOi (rojo) compuesto por la semirrecta [Oi) y la semirrecta [Oh) ambas con origen O.
Dos ángulos opuestos por el vértice son dos figuras geométricas distintas. Para resaltar esto, en la figura 1 se ha coloreado el ángulo fOg de color azul, mientras el ángulo hOi se ha coloreado de rojo.
Los ángulos azul y rojo de la figura 1 son opuestos por el vértice porque: la semirrecta [Of) del ángulo azul es la prolongación de la semirrecta [Oh) del ángulo rojo y la semirrecta [Og) del ángulo azul es la prolongación de la semirrecta [Oi) del ángulo rojo.
Índice del artículo
- 1 Conceptos importantes sobre ángulos
- 2 Rectas perpendiculares y ángulo recto
- 3 Medida de un ángulo
- 4 Teorema de los ángulos opuestos por el vértice
- 5 Ejercicio resuelto
- 6 Referencias
La figura geométrica que consta de dos semirrectas con origen común es un ángulo. En la siguiente imagen se muestra el ángulo POQ formado por las dos semirrectas [OP) y [OQ) de origen común O:
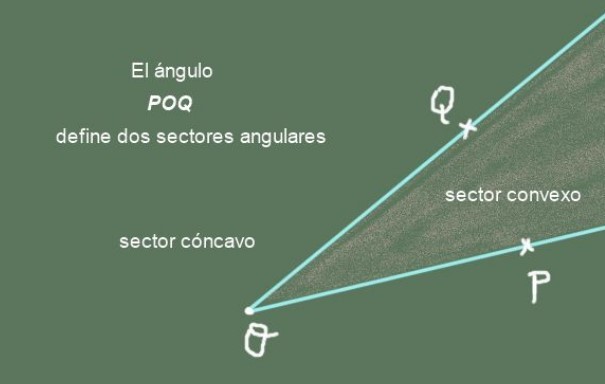
Las semirrectas [OP) y [OQ) son los lados del ánguloPOQ, mientras que el punto común O se denomina vértice del ángulo.
Sector angular: Un ángulo divide al plano que lo contiene en dos sectores angulares. Uno de ellos es el sector angular convexo y el otro es el sector angular cóncavo. La unión de los dos sectores da el plano completo.
La figura 2 muestra al ángulo POQ y sus dos sectores angulares. El sector angular convexo es el que tiene forma puntiaguda, mientras que el cóncavo es el sector angular del plano que le falta el sector convexo.
Dos rectas de un plano que se interceptan forman cuatro ángulos y dividen al plano en cuatro sectores angulares.
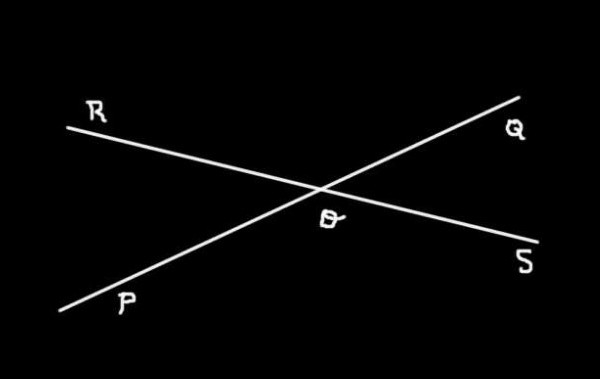
La figura 3 muestra las dos rectas (PQ) y (RS) que se interceptan en O. Allí puede verse que se determinan cuatro ángulos:
-SOQ, QOR, ROP y POS
Los ángulos SOQ y QOR, QOR y ROP, ROP y POS, POS y SOQ son ángulos adyacentes entre sí, mientras que SOQ y ROP son opuestos por el vértice. También son ángulos opuestos por el vértice los ángulos QOR y POS.
Dos rectas secantes (rectas que se intersectan) son rectas perpendiculares si determinan cuatro sectores angulares de igual medida. Si cada uno de los cuatro sectores son simétricos con el sector angular adyacente, entonces tienen la misma medida.
Cada uno de los ángulos que determinan las dos rectas perpendiculares se denomina ángulo recto. Todos los ángulos rectos tienen la misma medida.
Dada una recta y un punto de ella se definen dos semirrectas. Esas dos semirrectas definen dos ángulos planos.
En la figura 3 puede observarse la recta (RS) y el punto O que pertenece a (RS). El ángulo SOR es un ángulo plano. También puede afirmarse que el ángulo ROS es un ángulo plano. Todos los ángulos planos tienen la misma medida.
Una sola semirrecta define dos ángulos: uno de ellos el del sector angular convexo es el ángulo nulo y el otro, el del sector angular cóncavo es el ángulo completo. En la figura 3 puede verse el ángulo nulo SOS y el ángulo completo SOS.
Hay dos sistemas numéricos que se usan frecuentemente para dar la medida de un ángulo.
Uno de ellos es el sistema sexagesimal, es decir en base al número 60. Es una herencia de las antiguas culturas mesopotámicas. El otro sistema de medida de ángulos es el sistema radián, basado en número π (pi) y es un legado de los antiguos sabios griegos que desarrollaron la geometría.
Ángulo nulo: en el sistema sexagesimal el ángulo nulo mide 0º (cero grados).
Ángulo completo: se le asigna la medida 360º (trescientos sesenta grados).
Ángulo plano: en el sistema sexagesimal el ángulo plano mide 180º (ciento ochenta grados).
Ángulo recto: dos rectas perpendiculares dividen el plano en cuatro ángulos de igual medida llamados ángulos rectos. La medida de un ángulo recto es la cuarta parte del ángulo completo, es decir 90º (noventa grados).
Transportador o goniómetro
El transportador es el instrumento que se usa para medir ángulos. Consiste en un semicírculo (por lo general de plástico transparente) dividido en 180 secciones angulares. Como un semicírculo forma un ángulo plano, entonces la medida entre dos secciones consecutivas es 1º.
El goniómetro es similar al transportador y consiste en un círculo dividido en 360 secciones angulares.
Un ángulo cuyos lados parten del centro del goniómetro interceptan dos sectores y la medida de ese ángulo en grados es igual al número n de secciones comprendidas entre los dos sectores interceptados, en este caso la medida será nº (se lee “ene grados”).
Formalmente, el teorema se enuncia de esta manera:
Si dos ángulos son opuestos por el vértice, entonces tienen la misma medida.
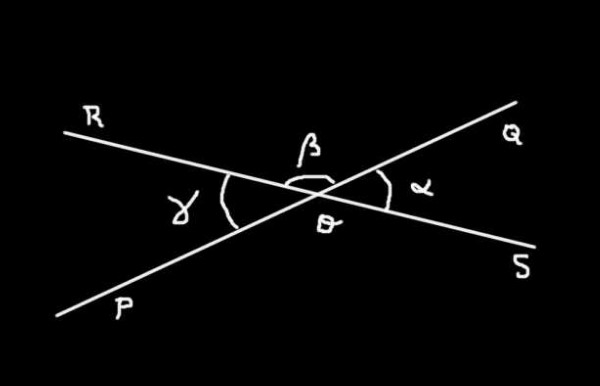
El ángulo SOQ tiene medida α; el ángulo QOR tiene medida β y el ángulo ROP tiene medida γ. La suma del ángulo SOQ más el QOR forma el ángulo plano SOR de medida 180º.
Es decir que:
α + β = 180º
Por otra parte y usando el mismo razonamiento con los ángulos QOR y ROP se tiene:
β + γ = 180º
Si observamos las dos ecuaciones anteriores, la única manera que ambas se cumplan es que α sea igual a γ.
Como SOQ tiene medida α y es opuesto por el vértice a ROP de medida γ, y como α = γ, se concluye que los ángulos opuestos por el vértice tienen la misma medida.
En referencia a la figura 4: suponga que β = 2 α. Encuentre la medida de los ángulos SOQ, QOR y ROP en grados sexagesimales.
Como la suma del ángulo SOQ más el QOR forma el ángulo plano SOR se tiene:
α + β = 180º
Pero nos dicen que β = 2 α. Sustituyendo este valor de β nos queda:
α + 2 α = 180º
Es decir:
3 α = 180º
Lo que significa que α es la tercera parte de 180º:
α = (180º / 3) = 60º
Entonces la medida de SOQ es α = 60º. La medida de QOR es β = 2 α = 2*60º = 120º. Por último como ROP es opuesto por el vértice a SOQ entonces de acuerdo al teorema ya demostrado tienen la misma medida. Es decir, la medida de ROP es γ = α = 60º.
- Baldor, J. A. 1973.Geometría plana y del espacio. Cultural centroamericana.
- Leyes y fórmulas matemáticas. Sistemas de medida de ángulos. Recuperado de: ingemecanica.com.
- Wikipedia. Ángulos opuestos por el vértice. Recuperado de: es.wikipedia.com
- Wikipedia. Transportador. Recuperado de: es.wikipedia.com
- Zapata F. Goniómetro: historia, partes, funcionamiento. Recuperado de: lifeder.com
