Teorema de Bolzano: concepto, explicación, aplicaciones, ejercicios

¿Qué es el teorema de Bolzano?

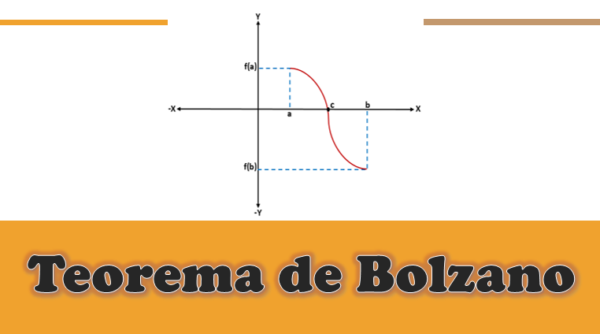
El teorema de Bolzano establece que si una función es continua en todos los puntos de un intervalo cerrado [a, b] y se cumple que la imagen de “a” y “b” (bajo la función) tienen signos opuestos, entonces existirá por lo menos un punto “c” en el intervalo abierto (a, b), de tal manera que la función evaluada en “c” será igual a 0.

Este teorema fue enunciado por el filósofo, teólogo y matemático Bernard Bolzano en 1850. Este científico, nacido en la actual República Checa, fue uno de los primeros matemáticos  en la historia en hacer una demostración formal de las propiedades de las funciones continuas.

Explicación del teorema

El teorema de Bolzano es conocido también como el teorema de los valores intermedios, el cual ayuda en la determinación de valores específicos, particularmente ceros, de ciertas funciones reales de una variable real.

En una función dada f(x) continua —es decir, que f(a) y f(b) están conectados por una curva—, donde f(a) está por debajo del eje x (es negativa), y f(b) por encima del eje x (es positiva), o viceversa, gráficamente existirá un punto de corte en el eje x que representará un valor intermedio “c”, que estará entre “a” y “b”, y el valor de f(c) será igual a 0.

Al analizar gráficamente el teorema de Bolzano, se puede saber que para toda función f continua definida en un intervalo [a, b], donde f(a)_*f(b) sea menor que 0, existirá por lo menos una raíz “c” de esa función dentro del intervalo (a,b).

Este teorema no establece el número de puntos existentes en ese intervalo abierto, solo afirma que existe como mínimo 1 punto.

Demostración del teorema de Bolzano

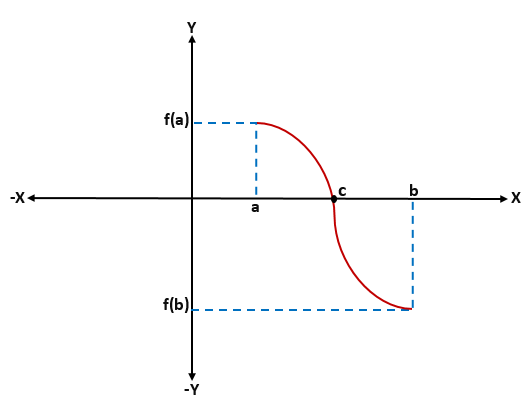
Para demostrar el teorema de Bolzano se supone sin pérdida de generalidad que f(a) 0 y f(b) > 0; de esa forma, pueden existir muchos valores entre “a” y “b” para los que f(x) = 0, pero solo se necesita demostrar que existe uno.

Se comienza evaluando f en el punto medio (a+b)/2. Si f((a+b)/2)=0 entonces la prueba termina aquí; en caso contrario, entonces f((a+b)/2) es positivo o negativo.

Se escoge una de las mitades del intervalo [a,b], tal que los signos de la función evaluada en los extremos son diferentes. Este nuevo intervalo será [a1, b1].

Ahora, si f evaluada en el punto medio de [a1, b1] no es cero, entonces se realiza la misma operación de antes; es decir, se escoge una mitad de este intervalo que cumpla la condición de los signos. Sea este nuevo intervalo [a2,b2].

Si se continúa con este proceso, entonces se tendrán dos sucesiones {an} y {bn}, tal que:

{an} es creciente y {bn} es decreciente:

a ≤ a1 ≤ a2 ≤ … ≤ an ≤ …. ≤ …. ≤ bn ≤ …. ≤ b2 ≤ b1 ≤ b.

Si se calcula la longitud de cada intervalo [ai, bi], se tendrá que:

b1-a1 = (b-a)/2.

b2-a2 = (b-a)/2².

….

bn-an = (b-a)/2^n.

Por lo tanto, el límite cuando n tiende a infinito de (bn-an) es igual a 0.

Utilizando que {an} es creciente y acotada y {bn} es decreciente y acotada, se tiene que existe un valor “c” tal que:

a ≤ a1 ≤ a2 ≤ … ≤ an ≤ ….≤ c ≤ …. ≤ bn ≤ …. ≤ b2 ≤ b1 ≤ b.

El límite de an es “c” y el límite de {bn} también es “c”. Por lo tanto, dado cualquier δ>0, siempre existe un “n” tal que el intervalo [an, bn] está contenido dentro del intervalo (c-δ, c+δ).

Ahora, se debe demostrar que f(c)=0.

Si f(c) > 0, entonces como f es continua, existe un ε >0 tal que f es positiva en todo el intervalo (c–ε , c+ε). Sin embargo, según lo dicho anteriormente, existe un valor “n” tal que f cambia de signo en [an, bn] y, además, [an, bn] está contenido dentro de (c–ε , c+ε), lo cual es una contradicción.

Si f(c) 0, entonces como f es continua, existe un ε >0 tal que f es negativa en todo el intervalo (c–ε , c+ε); pero existe un valor “n” tal que f cambia de signo en [an, bn]. Resulta que [an, bn] está contenido dentro de (c–ε , c+ε), lo cual también es una contradicción.

Por lo tanto, f(c)=0 y esto es lo que se quería demostrar.

¿Para qué sirve el teorema de Bolzano?

A partir de su interpretación gráfica, el teorema de Bolzano es utilizado para encontrar raíces o ceros en una función continua, a través de la bisección (aproximación), el cual es un método de búsqueda incremental que siempre divide los intervalos en 2.

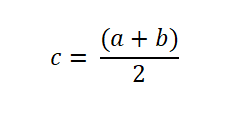
Luego se toma un intervalo [a, c] o [c, b] donde ocurre el cambio de signo, y se repite el proceso hasta que el intervalo sea cada vez menor, para así poder aproximarse al valor que se quiere; es decir, al valor que hace 0 la función.

En resumen, para aplicar el teorema de Bolzano y así hallar las raíces, acotar los ceros de una función o darle solución a una ecuación, se realizan los siguientes pasos:

1. Se verifica si f es una función continua en el intervalo [a, b].
2. Si el intervalo no es dado, se debe hallar uno donde la función sea continua.
3. Se verifica si los extremos del intervalo dan signos opuestos al ser evaluados en f.
4. Si no se obtienen signos opuestos, el intervalo debe ser dividido en dos subintervalos usando el punto medio.
5. Evaluar la función en el punto medio y verificar que se cumple la hipótesis de Bolzano, donde f(a) _* f (b) 0.
6. Dependiendo del signo (positivo o negativo) del valor hallado, se repite el proceso con un nuevo subintervalo hasta que se cumpla la hipótesis mencionada.

Ejercicios resueltos

Ejercicio 1

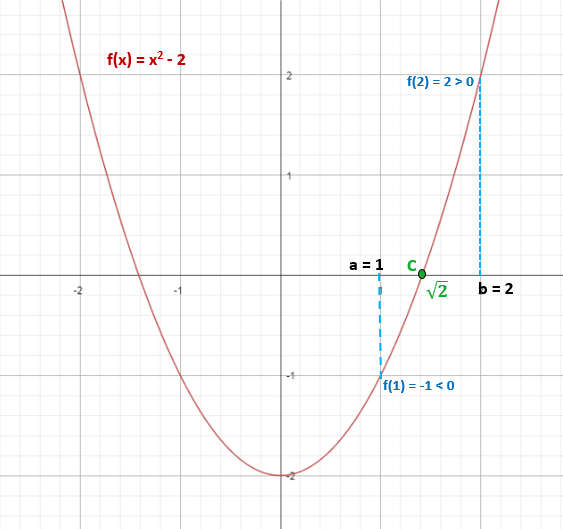
Determinar si la función f(x) = x² – 2, tiene al menos una solución real en el intervalo [1,2].

Solución

Se tiene la función f(x) = x² – 2. Como es polinómica, significa que es continua en cualquier intervalo.

Se pide determinar si tiene una solución real en el intervalo [1, 2], por lo que ahora solo se necesita sustituir los extremos del intervalo en la función para saber el signo de estos y saber si cumplen con la condición de ser diferentes:

f(x) = x² – 2

f(1) = 1² – 2 = -1 (negativo)

f(2) = 2² – 2 = 2 (positivo)

Por lo tanto, signo de f(1) ≠ signo f(2).

Esto asegura que sí existe al menos un punto “c” que pertenece al intervalo [1,2], en el que f(c) = 0.

En este caso se puede calcular de forma sencilla el valor de “c” como sigue:

x² – 2 = 0

x = ±√2.

Así, √2 ≈ 1,4 pertenece al intervalo [1,2] y cumple que f(√2)=0.

Ejercicio 2

Demostrar que la ecuación x⁵ + x + 1 = 0 tiene al menos una solución real.

Solución

Primero notemos que f(x) = x⁵ + x + 1 es una función polinómica, lo que significa que es continua en todos los números reales.

En este caso no es dado ningún intervalo, por eso se deben elegir valores intuitivamente, preferiblemente cercanos a 0, para evaluar la función y hallar los cambios de signo:

Si se usa el intervalo [0, 1] se tiene que:

f(x) = x⁵ + x + 1.

f(0) = 0⁵ + 0 + 1 = 1> 0.

f(1) = 1⁵ + 1 + 1 = 3> 0.

Como no hay cambio de signo, se repite el proceso con otro intervalo.

Si se utiliza el intervalo [-1, 0] se tiene que:

f(x) = x⁵ + x + 1.

f(-1) = (-1)⁵ + (-1) + 1 = -1 0.

f(0) = 0⁵ + 0 + 1 =  1 > 0.

En este intervalo existe un cambio de signo: signo de f(-1) ≠ signo de f(0), lo que significa que la función f(x)=x⁵ + x + 1 tiene al menos una raíz real “c” en el intervalo [-1, 0], tal que f(c) = 0. En otras palabras, se cumple que x⁵ + x + 1=0 tiene una solución real en el intervalo [-1,0].