Teorema de Varignon (mecánica): demostración, ejemplo, ejercicios
¿Qué es el teorema de Varignon?
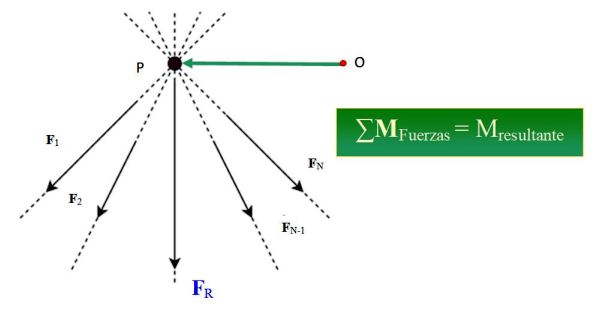
El teorema de Varignon, en Mecánica, afirma que la suma de los momentos producidos por un sistema de fuerzas concurrentes respecto a un determinado punto, es igual al momento de la fuerza resultante respecto al mismo punto.
Por esta razón también se conoce a este teorema como el principio de los momentos.
Si bien el primero en enunciarlo fue el holandés Simon Stevin (1548-1620), el creador de la paradoja hidrostática, el matemático francés Pierre Varignon (1654-1722) fue quien posteriormente le dio su forma definitiva.
Un ejemplo de cómo funciona el teorema de Varignon en Mecánica es el siguiente: supóngase que sobre un punto actúa un sistema simple de dos fuerzas coplanares y concurrentes F1 y F2, (denotadas con negritas por su carácter vectorial). Dichas fuerzas dan lugar a una fuerza neta o resultante, llamada FR.
Cada fuerza ejerce un torque o momento respecto a un punto O, que se calcula mediante el producto vectorial entre el vector de posición rOP y la fuerza F, donde rOP va dirigido desde O hasta el punto de concurrencia P:
MO1 = rOP × F1
MO2 = rOP × F2
Dado que FR = F1 + F2, entonces:
MO = rOP × F1 + rOP × F2 = MO1 + MO2
Pero como rOP es factor común, entonces, aplicando propiedad distributiva al producto cruz:
MO = rOP × (F1 + F2) = rOP × FR
Por lo tanto, la suma de los momentos o torques de cada fuerza respecto al punto O, equivale al momento de la fuerza resultante respecto al mismo punto.
Enunciado y demostración
Sea un sistema de N fuerzas concurrentes, formado por F1, F2, F3… FN, cuyas líneas de acción se cruzan en el punto P (ver la figura 1), el momento de este sistema de fuerzas MO, respecto a un punto O viene dado por:
MO = rOP × F1 + rOP × F2 + rOP × F3 + … rOP × FN = rOP × (F1 + F2 + F3 +… FN)
Demostración
Para demostrar el teorema se hace uso de la propiedad distributiva del producto vectorial entre vectores.
Sean las fuerzas F1, F2, F3… FN aplicadas a los puntos A1, A2, A3… AN y concurrentes en el punto P. El momento resultante de este sistema, con respecto a un punto O, llamado MO, es la suma de los momentos de cada fuerza, respecto a dicho punto:
MO = ∑ rOAi × Fi
Donde la suma va desde i = 1 hasta i = N, puesto que hay N fuerzas. Como se trata de fuerzas concurrentes y dado que el producto vectorial entre vectores paralelos es nulo, ocurre que:
rPAi × Fi = 0
Con el vector nulo denotado como 0.
El momento de una de las fuerzas respecto a O, por ejemplo el de la fuerza Fi aplicada en Ai, se escribe así:
MOi = rOAi × Fi
El vector de posición rOAi se puede expresar como la suma de dos vectores posición:
rOAi = rOP + rPAi
De esta manera, el momento respecto a O de la fuerza Fi es:
MOi = (rOP + rPAi) × Fi = (rOP × Fi) + (rPAi × Fi)
Pero el último término es nulo, como se explicó más arriba, porque rPAi se encuentra sobre la línea de acción de Fi, por lo tanto:
MOi = rOP × Fi
Sabiendo que el momento del sistema respecto al punto O es la sumatoria de todos los momentos individuales de cada fuerza respecto a dicho punto, entonces:
MO = ∑ MOi = ∑ rOP × Fi
Como rOP es constante sale fuera de la suma:
MO = rOP × (∑ Fi)
Pero ∑ Fi es simplemente la fuerza neta o fuerza resultante FR, por lo tanto se concluye de inmediato que:
MO = rOP × FR
Ejemplo
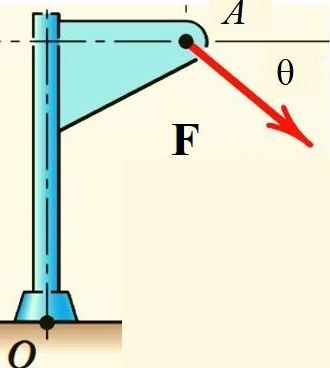
El teorema de Varignon facilita el cálculo del momento de la fuerza F respecto al punto O en la estructura mostrada en la figura, si se descompone la fuerza en sus componentes rectangulares y se calcula el momento de cada una de ellas:
Aplicaciones del teorema de Varignon
Cuando se conoce la fuerza resultante de un sistema, el teorema de Varignon se puede aplicar para reemplazar la suma de cada uno de los momentos producidos por las fuerzas que lo componen por el momento de la resultante.
Si el sistema consta de fuerzas sobre un mismo plano y el punto respecto al cual se quiere calcular el momento pertenece a ese plano, el momento resultante es perpendicular.
Por ejemplo, si todas las fuerzas están en el plano xy, el momento está dirigido en el eje z y solo resta hallar su magnitud y su sentido, tal es el caso del ejemplo antes descrito.
En ese caso el teorema de Varignon permite calcular el momento resultante del sistema a través de la sumatoria. Es muy útil en el caso de un sistema de fuerzas tridimensional, para el cual no se sabe a priori la dirección del momento resultante.
Para resolver estos ejercicios conviene descomponer fuerzas y vectores de posición en sus componentes rectangulares, y a partir de la sumatoria de los momentos, determinar las componentes del momento neto.
Ejercicio resuelto
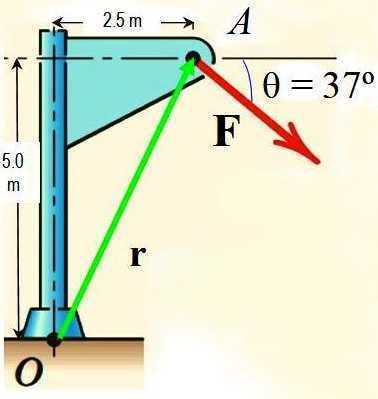
Mediante el teorema de Varignon, calcular el momento de la fuerza F alrededor del punto O mostrado en la figura si la magnitud de F es 725 N.
Solución
Para aplicar el teorema de Varignon se descompone la fuerza F en dos componentes, cuyos respectivos momentos alrededor de O se calculan y se suman para obtener el momento resultante.
Fx = 725 N ∙ cos 37 º = 579.0 N
Fy = − 725 N N ∙ sen 37 º = −436.3 N
De igual manera, el vector de posición r dirigido desde O hasta A tiene las componentes:
rx = 2.5 m
ry = 5.0 m
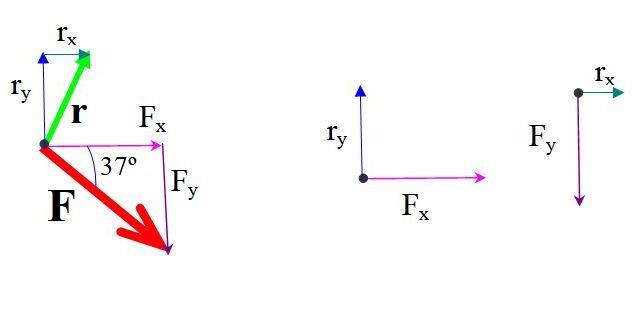
El momento de cada componente de la fuerza respecto a O se halla multiplicando la fuerza y la distancia perpendicular.
Ambas fuerzas tienden a hacer girar la estructura en el mismo sentido, que en este caso es el sentido horario, al cual se le asigna arbitrariamente signo positivo:
MOx = Fx∙ ry ∙ sen 90º = 579.0 N ∙ 5.0 m = 2895 N∙m
MOy = Fy∙ rx ∙ sen (−90º) = −436.3 N ∙ 2.5 m ∙ (−1) = 1090.8 N∙m
El momento resultante respecto a O es:
MO = MOx + MOy = 3985.8 N∙m perpendicular al plano y en sentido horario.
Referencias
- Bedford, 2000. A. Mecánica para Ingeniería: Estática. Addison Wesley.
- Beer, F. 2010. Estática. McGraw Hill. 9na. Edición.
- Hibbeler, R. 1992. Mecánica para ingenieros. 6ta. Edición. CECSA.
- HK Ingeniería. Teorema de Varignon. Recuperado de: youtube.com.
- Wikipedia. Varignon’s theorem (Mechanics). Recuperado de: en.wikipedia.org.
