Rectas secantes: qué son, características, tipos y ejemplos

¿Qué son las rectas secantes?

En el plano, las rectas secantes son aquellas que intersectan a otras rectas y curvas. Tratándose de dos rectas, su intersección es un punto, mientras que la recta secante a una curva, corta a esta en dos o más puntos.

Obsérvese cuidadosamente la valla de la figura superior. Sobre ella se han dibujado varias rectas de colores distintos, denotadas como L₁, L₂ y L₃. Las flechas en ambos lados significan que las rectas se prolongan indefinidamente.

Pues bien, las rectas L₁, L₂ y L₃ son secantes entre sí, ya que cada par de ellas se corta en los puntos de color morado.

Además, las rectas L₁ y L₂, al igual que L₁ y L₃, determinan 4 ángulos entre sí, dos de ellos agudos y los otros obtusos, mientras que las rectas L₂ y L₃ son perpendiculares, lo que significa que los 4 ángulos determinados por ellas son rectos.

Dos rectas paralelas nunca pueden ser secantes, ya que, por su condición, no tienen puntos de coincidencia. A su vez, las rectas coincidentes no son secantes, pues tienen más de un punto en común.

Características de las rectas secantes

• Dos rectas secantes tienen un punto único como intersección.
• Las pendientes de dos rectas secantes deben ser diferentes. Si m₁ es la pendiente de la recta L₁, y m₂ es la pendiente de la recta L₂, entonces se cumple que m₁ ≠ m₂.
• Las pendientes de dos rectas secantes perpendiculares entre sí, cuyas pendientes respectivas son m₁ y m₂, cumplen la relación m₁ = -1/ m₂. Además, el producto escalar entre dos vectores v y u contenidos en dichas rectas es nulo, puesto que la definición de producto escalar es vu = v∙u∙cos θ, siendo θ el ángulo entre los vectores.
• Una recta puede ser secante a una curva o a otra figura geométrica.
• Al intersectarse, dos rectas secantes generan 4 ángulos, idénticos dos a dos o bien idénticos entre sí.

Cómo saber si dos rectas son secantes

A partir de las características de las rectas secantes antes descritas, es posible establecer tres criterios para saber si dos rectas son secantes:

-Comparando las pendientes. Si estas son diferentes, las rectas son secantes.

-Llevando a cabo el producto escalar entre dos vectores que estén contenidos en dichas rectas, llamados vectores directores. Si el producto escalar es nulo, las rectas son secantes y perpendiculares, y si es no nulo, es posible conocer el ángulo mínimo entre ellos, que es el ángulo agudo existente entre las rectas.

Siempre que dicho ángulo sea distinto a 0º, las rectas son secantes, y si es igual a 0º, entonces se trata de rectas paralelas.

-Calculando directamente el ángulo agudo que existe entre las rectas, conocidas sus pendientes. Esto se puede hacer a través de la fórmula que relaciona la tangente de dicho ángulo con las pendientes.

Sean m₁ y m₂ las pendientes, y θ el ángulo agudo entre ellas. La tangente de θ viene dada por:

Tipos de rectas secantes

Cuando dos rectas son secantes entre sí, pueden ser de los siguientes tipos:

• Oblicuas, si al cortarse forman dos ángulos agudos y dos ángulos obtusos. Dichos ángulos son suplementarios, es decir, la suma de la medida del ángulo más la del ángulo obtuso es igual a 180º. En total, la suma de los 4 ángulos es igual a 360º.
• Perpendiculares, aquellas que al intersectarse determinan 4 ángulos iguales a 90º.

Cómo encontrar la intersección entre dos rectas

Si dos rectas son secantes, tienen un solo punto de corte, el cual se encuentra resolviendo el sistema de dos ecuaciones lineales con dos incógnitas. Si las rectas están dadas en forma general: ax + by = c, dicho sistema de ecuaciones es:

a₁x + b₁ y = c₁

a₂x + b₂ y = c₂

Cómo encontrar la intersección entre una recta y una curva

Conociendo las ecuaciones tanto de la recta como de la curva, se plantea el sistema de ecuaciones y, cuyas soluciones corresponden a los puntos de intersección. Si el sistema carece de solución, la recta no es secante a la curva, como tampoco lo es si existe un único punto de corte, ya que, en tal caso, la recta es tangente a la curva.

Para que la recta sea secante, tal como se dijo al principio, el sistema de ecuaciones debe tener dos o más soluciones.

Ejemplos de rectas secantes

El plano cartesiano

El plano cartesiano está determinado por dos rectas, llamadas eje x y eje y, horizontal y vertical, respectivamente. Dichas rectas son perpendiculares y su punto de intersección se denomina origen del sistema de coordenadas, o simplemente origen.

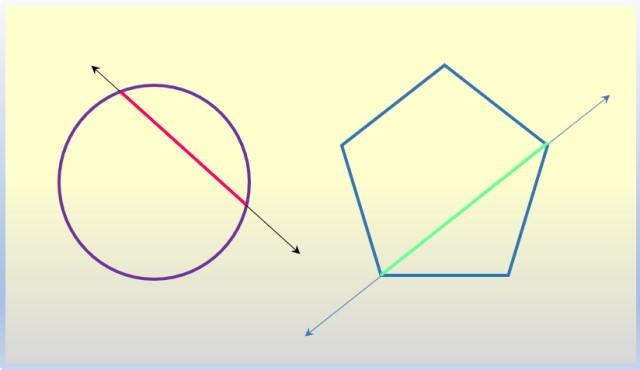
La diagonal de un polígono

Un polígono es una figura plana de tres o más lados, los cuales se unen en puntos llamados vértices. Un segmento que une dos vértices no consecutivos es una diagonal del polígono, y la recta que contiene dicho segmento es secante al polígono en cuestión.

Una cuerda de circunferencia

La cuerda de una circunferencia es el segmento que une dos de sus puntos. La cuerda mayor es el diámetro, que necesariamente pasa por el centro de la circunferencia. Pues bien, la recta que contiene a una cuerda cualquiera, incluido el diámetro, es una recta secante a la circunferencia.

La llave de cruz

Con esta herramienta se aflojan las tuercas que sujetan los neumáticos a las ruedas de los vehículos. Los brazos forman entre sí líneas que son secantes y la vez perpendiculares.

Letras del alfabeto

Algunas letras del alfabeto consisten en trazos rectos que determinan secantes. Por ejemplo, la letra X consta de dos trazos que se cortan entre sí en un solo punto y la letra T consta de dos líneas perpendiculares.

Ejercicios resueltos

Ejercicio 1

Determinar si son secantes las rectas dadas por:

L₁ : y = 5x – 3

L₂ : y = –2x+1

Solución

La pendiente de una recta dada en la forma y = mx + b es el valor de m, es decir, el coeficiente que acompaña a la x. Puesto que m₁ = 5 y m₂ = –2, los cuales son diferentes, se concluye que las rectas son secantes.

Ejercicio 2

¿Cuál es el ángulo agudo entre las rectas del ejercicio 1?

Solución

Se sustituyen directamente los valores m₁ = 5 y m₂ = –2 en la fórmula dada en las secciones precedentes:

Por lo tanto, el ángulo entre las rectas es θ = arctg 0.777… = 37.9º.

Ejercicio 3

¿Cuál es la intersección entre las rectas de los ejercicios anteriores?

Solución

Se plantea el sistema de ecuaciones de la siguiente forma:

Cuya solución es: x = 4/7; y = –1/7 (puede resolverse por cualquiera de los métodos de resolución para sistemas de ecuaciones, o bien con una calculadora).

Por lo tanto, el punto de intersección de las rectas es: P (4/7 ; –1/7).

Referencias

1. GeometríaAnalítica.info. Rectas secantes. Recuperado de: geometriaanalitica.info.
2. Larson, R. 2006. Cálculo con Geometría Analítica. 8va. Edición. McGraw Hill.
3. Rectas que se cruzan. Recuperado de: profesoraltuna.com.
4. Requena, B. Rectas secantes. Recuperado de: universoformulas.com.
5. Villena, M. Geometría Analítica en R3. Recuperado de: dspace.espol.edu.ec.