¿Cuál es la Diferencia entre Trayectoria y Desplazamiento?

La diferencia principal entre trayectoria y desplazamiento es que este último es la distancia y dirección recorrida por un objeto, mientras que la primera es la ruta o la forma que adopta el movimiento de ese objeto.

No obstante, para ver de forma más clara las diferencias entre desplazamiento y trayectoria, es mejor especificar su conceptualización a través de ejemplos que permitan una mayor comprensión de ambos términos.

Desplazamiento

Es entendido como la distancia y dirección recorrida por un objeto tomando en cuenta su posición inicial y su posición final, siempre en línea recta. Para su cálculo, por ser una magnitud vectorial, se utilizan las medidas de longitud conocidas como centímetros, metros o kilómetros.

La fórmula para calcular el desplazamiento está definida de la siguiente manera:

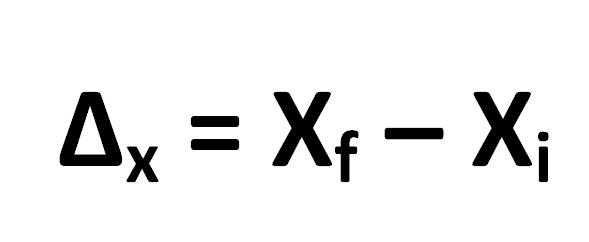
De la cual se desprende que:

• Δ_x =desplazamiento
• X_f = posición final del objeto
• X_i =posición inicial del objeto

Ejemplo de desplazamiento

1- Si un grupo de niños se encuentran al inicio de un recorrido, cuya posición inicial es de 50m, moviéndose en línea recta, determinar el desplazamiento en cada uno de los puntos X_f . 

• X_f = 120m
• X_f = 90m
• X_f = 60m
• X_f = 40m

2- Se extraen los datos del problema sustituyendo los valores de X₂ y X₁ en la fórmula de desplazamiento:

• Δ_x = ?
• X_i = 50m
• Δ_x = X_f – X_i
• Δ_x = 120m – 50m = 70m

3- En este primer planteamiento decimos que Δ_x es igual a 120m, que corresponde al primer valor que encontramos de X_f, menos 50m que es el valor de X_i, nos da como resultado 70m, es decir, al llegar a los 120m recorridos el desplazamiento fue de 70m hacia la derecha.

4- Procedemos a resolver de igual forma para los valores de b, c y d

• Δ_x = 90m – 50m = 40m
• Δ_x = 60m – 50m = 10m
• Δ_x = 40m – 50m = – 10m

En este caso el desplazamiento nos dio negativo, eso quiere decir que la posición final está en sentido contrario a la posición inicial.

Trayectoria

Es la ruta o línea determinada por un objeto durante su movimiento y su valoración en el Sistema Internacional, generalmente adopta formas geométricas como la recta, parábola, círculo o elipse). Se identifica a través de una línea imaginaria y por ser una cantidad escalar se mide en metros.

Cabe destacar que para calcular la trayectoria debemos saber si el cuerpo está en reposo o movimiento, es decir, se somete al sistema de referencia que seleccionemos.

La ecuación para calcular la trayectoria de un objeto en el Sistema Internacional viene dada por:

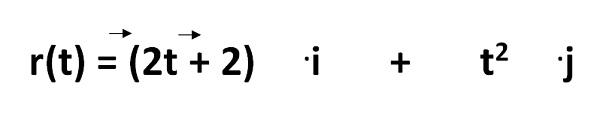
De la cual tenemos que:

• r(t) = es la ecuación de la trayectoria
• 2t – 2 y t² = representan las coordenadas en función del tiempo
• ^.i y ^.j = son los vectores unitarios

Para entender el cálculo de la trayectoria recorrida por un objeto vamos a desarrollar el siguiente ejemplo:

• Calcular la ecuación de las trayectorias de los siguientes vectores de posición:

1. r(t) = (2t + 7) ^.i + t^2.j
2. r(t) = (t – 2) ^.i + 2t ^.j

Primer paso: Como una ecuación de trayectoria es una función de X, para ello definir los valores de X y Y respectivamente en cada uno de los vectores planteados:

1- Resolver el primer vector de posición:

• r(t) = (2t + 7) ^.i + t^2.j

2- Ty=f(x), donde X viene dada por el contenido del vector unitario ^.i y Y viene dada por el contenido del vector unitario ^.j:

• X = 2t + 7
• Y = t²

3- y=f(x), es decir el tiempo no forma parte de la expresión por lo tanto debemos despejarlo, nos queda:

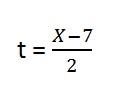
4- Sustituimos el despeje en Y. Se queda:

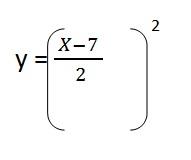
5- Resolvemos el contenido del paréntesis y tenemos la ecuación de la trayectoria resultante para el primer vector unitario:

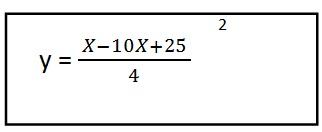
Como podemos observar nos dio como resultado una ecuación de segundo grado, esto quiere decir que la trayectoria tiene forma de parábola.

Segundo paso: Procedemos de igual forma para el cálculo de la trayectoria del segundo vector unitario

r(t) = (t – 2) ^.i + 2t ^.j

• X = t – 2
• Y = 2t

2- Siguiendo los pasos que vimos anteriormente y=f(x), debemos despejar el tiempo porque no forma parte de la expresión, nos queda:

• t = X + 2

3- Sustituimos el despeje en Y, quedándonos:

• y = 2 ( X + 2)

4- Resolviendo el paréntesis nos queda la ecuación de la trayectoria resultante para el segundo vector unitario:

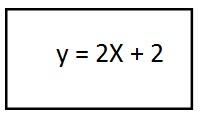
En este procedimiento nos dio como resultado una recta, lo cual nos dice que la trayectoria tiene forma rectilínea.

Entendidos los conceptos de desplazamiento y trayectoria podemos deducir el resto de diferencias que existen entre ambos términos.

Más diferencias entre desplazamiento y trayectoria

Desplazamiento

• Es la distancia y dirección recorrida por un objeto tomando en cuenta su posición inicial y su posición final.
• Siempre ocurre en línea recta.
• Se reconoce con una flecha.
• Utiliza medidas de longitud (centímetro, metro, kilómetro).
• Es una cantidad vectorial.
• Toma en cuenta el sentido recorrido (a la derecha o la izquierda)
• No considera el tiempo empleado durante el recorrido.
• No depende de un sistema de referencia.
• Cuando el punto de inicio es el mismo punto de partida, el desplazamiento es cero.
• El módulo debe coincidir con el espacio a recorrer siempre y cuando la trayectoria sea una línea recta y no se produzcan cambios en el sentido a seguir.
• El módulo tiende a aumentar o disminuir a medida que se da el movimiento, teniendo presente la trayectoria.

Trayectoria

Es la ruta o línea determinada por un objeto durante su movimiento. Adopta formas geométricas (recta, parabólica, circular o elíptica).

• Se representa a través de una línea imaginaria.
• Se mide en metros.
• Es una cantidad escalar.
• No toma en cuenta el sentido recorrido.
• Considera el tiempo empleado durante el recorrido.
• Depende de un sistema de referencia.
• Cuando el punto de partida o posición inicial es el mismo que la posición final, la trayectoria viene dada por la distancia recorrida.
• El valor de la trayectoria coincide con el módulo del vector desplazamiento, si la trayectoria resultante es una línea recta, pero no se produzcan cambios en el sentido a seguir.
• Siempre aumenta cuando el cuerpo se mueve, sin importar la trayectoria.

Referencias

1. Alvarado, N. (1972) Física. Primer Año de Ciencias. Editorial Fotoprin C.A. Venezuela.
2. Fernández, M; Fidalgo, J. (2016). Física y Química 1º Bachillerato. Ediciones Paraninfo, S.A. España.
3. Instituto Guatemalteco de Educación Radiofónica. (2011) Física fundamental. Primer Semestre Grupo Zaculeu. Guatemala.