¿Cuáles son los divisores de 30? (Explicación)

Los divisores de 30 son 1, 2, 3, 5, 6, 10, 15 y 30. Te explicamos por qué y cómo lo puedes calcular por ti mismo.

Rápidamente, puede saberse cuáles son los divisores de 30, así como de cualquier otro número (distinto de cero), pero la idea fundamental es aprender cómo se calculan los divisores de un número de manera general.

Debe tenerse cuidado cuando se habla de divisores, debido a que puede establecerse de manera rápida que todos los divisores de 30 son 1, 2, 3, 5, 6, 10, 15 y 30, pero ¿qué pasa con los negativos de estos números? ¿Son divisores o no?

Para dar respuesta a la pregunta anterior es necesario comprender un término muy importante en el mundo de las matemáticas: el algoritmo de la división.

Algoritmo de la división

El algoritmo de la división (o división euclidiana) dice lo siguiente: dados dos números enteros “n” y “b”, siendo “b” diferente de cero (b≠0), existen únicos enteros “q” y “r”, tales que n=bq+r, donde 0 ≤ r  |b|.

Al número “n” se le llama dividendo, a “b” se le llama divisor, a “q” se le llama cociente y a “r” se le llama el resto o residuo. Cuando el resto “r” es igual a 0 se dice que “b” divide a “n”, y esto se denota por “b|n”.

El algoritmo de la división no se restringe a valores positivos. Por tanto, un número negativo puede ser divisor de algún otro número.

¿Por qué 7,5 no es divisor de 30?

Usando el algoritmo de la división puede verse que 30=7,5×4+0. El resto es igual a cero, pero no puede decirse que 7,5 divide a 30 porque, cuando se habla de divisores, se está hablando solo de números enteros.

Divisores de 30

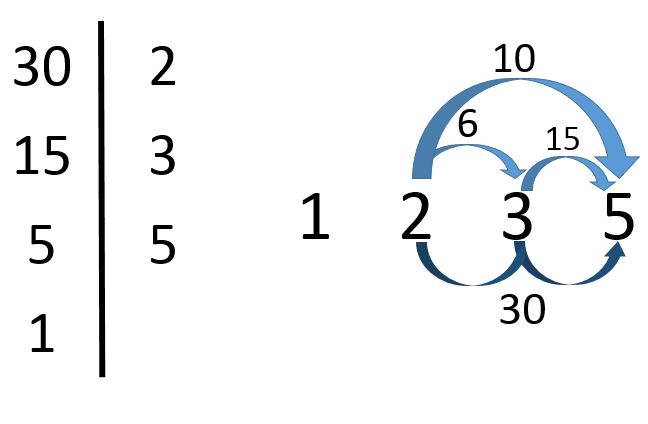
Como se aprecia en la imagen, para hallar los divisores de 30 primero deben encontrarse sus factores primos.

Entonces, 30=2x3x5. De aquí se concluye que 2, 3 y 5 son divisores de 30. Pero también lo son los productos de estos factores primos.

De modo que 2×3=6, 2×5=10, 3×5=15 y 2x3x5=30 son divisores de 30. El 1 también es un divisor de 30 (aunque en realidad es un divisor de cualquier número).

Puede concluirse que 1, 2, 3, 5, 6, 10, 15 y 30 son divisores de 30 (todos cumplen el algoritmo de la división), pero hay que recordar que sus negativos también son divisores.

Por lo tanto, todos los divisores de 30 son: -30, -15, -10, -6, -5, -3, -2, -1, 1, 2, 3, 5, 6, 10, 15 y 30.

Lo aprendido arriba puede aplicarse con cualquier número entero.

Por ejemplo, si se quieren calcular los divisores de 92, se procede como antes. Se descompone como un producto de números primos.

Se divide 92 entre 2 y se obtiene 46; ahora se divide 46 entre 2 nuevamente y se obtiene 23.

Este último resultado es un número primo, por lo que no tendrá más divisores además del 1 y el mismo 23.

Podemos entonces escribir 92=2x2x23. Procediendo como antes, se concluye que 1,2,4,46 y 92 son divisores de 92.

Por último, se incluyen los negativos de estos números a la lista anterior, con lo cual la lista de todos los divisores de 92 es -92, -46, -4, -2, -1, 1, 2, 4, 46, 92.