Cuadrilátero: elementos, propiedades, clasificación, ejemplos

Un cuadrilátero es un polígono de cuatro lados y cuatro vértices. Sus lados opuestos son los que no tienen vértices en común, mientras que son lados consecutivos los que tienen un vértice común.

En un cuadrilátero son ángulos adyacentes los que comparten un lado, mientras los ángulos opuestos no tienen lados en común. Otra característica importante de un cuadrilátero es que la suma de sus cuatro ángulos internos es dos veces el ángulo plano, es decir 360º o 2π radianes.

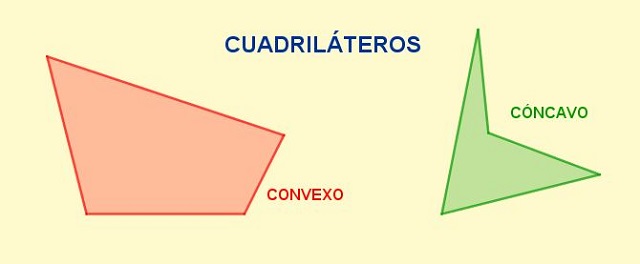
Las diagonales son los segmentos que unen un vértice con su opuesto y en un cuadrilátero dado, desde cada vértice se puede trazar una sola diagonal. El número total de diagonales de un cuadrilátero es dos.

Los cuadriláteros son figuras conocidas por la humanidad desde tiempos antiguos. Los registros arqueológicos, así como las construcciones que sobreviven hoy en día, dan fe de ello.

Igualmente en la actualidad los cuadriláteros siguen teniendo una importante presencia en la vida cotidiana de todos. El lector puede encontrar esta forma en la pantalla en la cual lee el texto en este preciso momento, en las ventanas, las puertas, las partes automotrices e incontables lugares más.

Índice del artículo

• 1 Clasificación de los cuadriláteros
  • 1.1 Tipos de paralelogramo
• 2 Trapecio
  • 2.1 Tipos de trapecios
• 3 Paralelogramo
  • 3.1 Área de un paralelogramo
  • 3.2 Diagonales de un paralelogramo
  • 3.3 Ley de los paralelogramos
• 4 Rectángulo
  • 4.1 Diagonales de un rectángulo
• 5 Cuadrado
• 6 Rombo
• 7 Ejemplos
  • 7.1 Ejemplo 1
  • 7.2 Ejemplo 2
  • 7.3 Ejemplo 3
• 8 Ejercicios resuelto
  • 8.1 – Ejercicio 1
  • 8.2 – Ejercicio 2
• 9 Referencias

Clasificación de los cuadriláteros

De acuerdo al paralelismo de los lados opuestos, los cuadriláteros se clasifican así:

1. Trapezoide, cuando no hay paralelismo y el cuadrilátero es convexo.
2. Trapecio, cuando hay paralelismo entre un solo par de lados opuestos.
3. Paralelogramo, cuando sus lados opuestos son paralelos dos a dos.

Tipos de paralelogramo

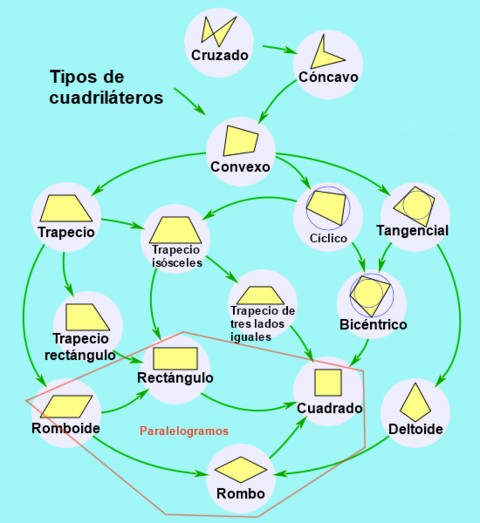
A su vez los paralelogramos pueden clasificarse según sus ángulos y sus lados de la siguiente manera:

1. Rectángulo, es el paralelogramo que tiene sus cuatro ángulos internos de igual medida. Los ángulos internos de un rectángulo forman un ángulo recto (90º).
2. Cuadrado, es un rectángulo con sus cuatro lados de igual medida.
3. Rombo, es el paralelogramo con sus cuatro lados iguales, pero sus ángulos adyacentes diferentes.
4. Romboide, paralelogramo con ángulos adyacentes distintos.

Trapecio

El trapecio es un cuadrilátero convexo con dos lados paralelos.

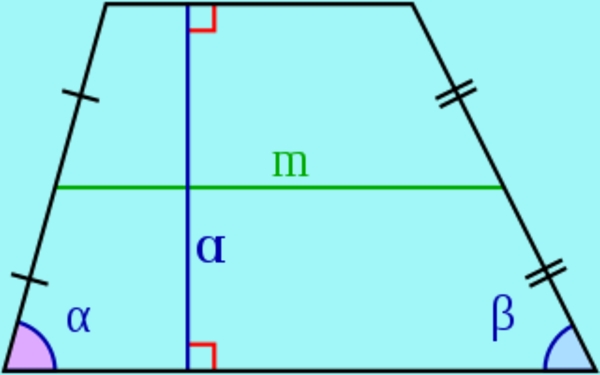
– En un trapecio los lados paralelos se llaman bases y los no paralelos se llaman laterales.

– La altura de un trapecio es la distancia que hay entre las dos bases, es decir la longitud de un segmento con extremos en las bases y perpendicular a las mismas. Dicho segmento también se le llama una altura del trapecio.

– La mediana es el segmento que une los puntos medios de las laterales. Se puede demostrar que la mediana es paralela a las bases del trapecio y su longitud es igual a la semisuma de las bases.

– El área de un trapecio es su altura multiplicada por la semisuma de las bases:

Área de un trapecio = altura * (base 1 + base 2) / 2

Tipos de trapecios

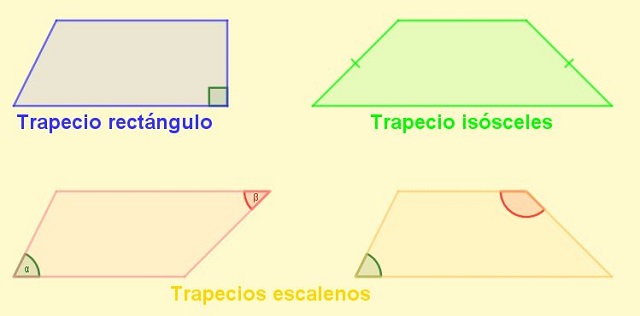
-Trapecio rectángulo: es el que tiene una lateral perpendicular a las bases. Dicha lateral también es altura del trapecio.

-Trapecio isósceles: el que tiene laterales de igual longitud. En un trapecio isósceles los ángulos adyacentes a las bases son iguales.

-Trapecio escaleno: el que tiene sus laterales de diferente longitud. Sus ángulos opuestos pueden ser uno agudo y el otro obtuso, pero también puede ocurrir que ambos sean obtusos o ambos agudos.

Paralelogramo

El paralelogramo es un cuadrilátero cuyos lados opuestos son paralelos dos a dos. En un paralelogramo los ángulos opuestos son iguales y los ángulos adyacentes son suplementarios, o dicho de otra manera, los ángulos adyacentes suman 180º.

Si un paralelogramo tiene un ángulo recto, entonces todos los otros ángulos también lo serán y la figura resultante se llama rectángulo. Pero si además el rectángulo tiene sus lados adyacentes de la misma longitud, entonces todos sus lados son iguales y la figura resultante es un cuadrado.

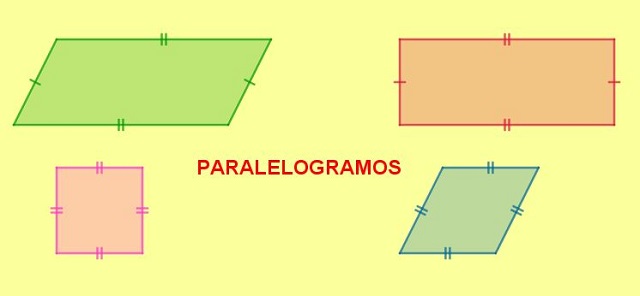
Cuando un paralelogramo tiene dos lados adyacentes de la misma longitud, todos sus lados serán de la misma longitud y la figura resultante es un rombo.

La altura de un paralelogramo es un segmento con extremos en sus lados opuestos y perpendicular a los mismos.

Área de un paralelogramo

El área de un paralelogramo es el producto de la base por su altura, siendo la base un lado perpendicular a la altura (figura 6).

Área de un paralelogramo = base x altura = a . h

Diagonales de un paralelogramo

El cuadrado de la diagonal que parte de un vértice es igual a la suma de los cuadrados de los dos lados adyacentes a dicho vértice más el doble producto de esos lados por el coseno del ángulo de ese vértice:

f² = a² +  d² + 2 a d Cos(α)

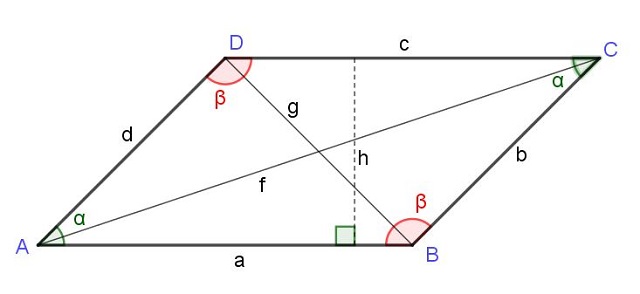
El cuadrado de la diagonal opuesta al vértice de un paralelogramo es igual a la suma de los cuadrados de los dos lados adyacentes a dicho vértice y restado el doble producto de esos lados por el coseno del ángulo de ese vértice:

g² = a² + d² – 2 a d Cos(α)

Ley de los paralelogramos

En cualquier paralelogramo la suma de los cuadrados de sus lados es igual a la suma de los cuadrados de las diagonales:

a² + b² + c² + d² = f² + g²

Rectángulo

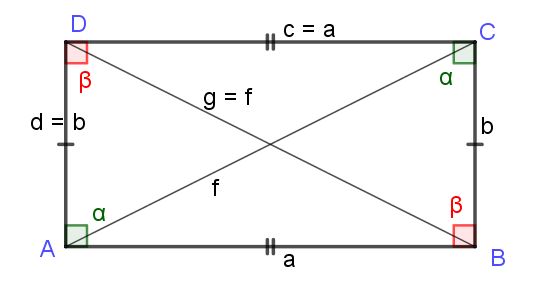
El rectángulo es un cuadrilátero con sus lados opuestos paralelos dos a dos y que además tiene un ángulo recto. Es decir que el rectángulo es un tipo de paralelogramo con un ángulo recto. Por ser paralelogramo, el rectángulo tiene sus lados opuestos de igual longitud a=c y b=d. 

Pero como en cualquier paralelogramo los ángulos adyacentes son suplementarios y los ángulos opuestos iguales, en el rectángulo por tener un ángulo recto, formará necesariamente ángulos rectos en los otros tres ángulos. Es decir en un rectángulo todos los ángulos internos miden 90º o π/2 radianes.

Diagonales de un rectángulo

En un rectángulo las diagonales son de igual longitud, como se demostrará a continuación. El razonamiento es el siguiente; un rectángulo es un paralelogramo con todos sus ángulos rectos y por eso hereda todas las propiedades del paralelogramo, incluida la fórmula que da la longitud de las diagonales:

f² = a²+  d² + 2 a d Cos(α)

g² = a² + d² – 2 a d Cos(α)

con α = 90º

Como Cos(90º) = 0, entonces ocurre que:

f² = g² = a² +  d²

Es decir que f = g, y por tanto las longitudes f y g de las dos diagonales del rectángulo son iguales y su longitud viene dada por:

Longitud de diagonales de un rectángulo = √( a² + b²)

Además, si en un rectángulo de lados adyacentes a y b un lado se toma como base el otro lado será altura y consecuentemente el área del rectángulo será:

Área del rectángulo = a x b.

El perímetro es la suma de todos los lados del rectángulo, pero como los opuestos son iguales se tiene entonces que para un rectángulo de lados a y b el perímetro viene dado por la siguiente fórmula:

Perímetro del rectángulo = 2 (a + b)

Cuadrado

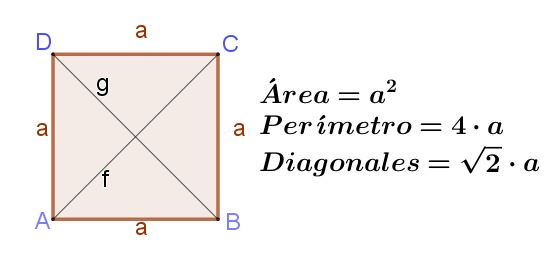
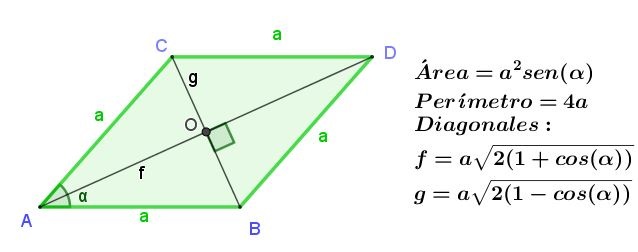
El cuadrado es un rectángulo con sus lados adyacentes de la misma longitud. Si el cuadrado tiene lado a, entonces sus diagonales f y g tienen la misma longitud, la cual es f = g = (√2) a.

El área de un cuadrado es su lado elevado al cuadrado:

Área de un cuadrado = a²

El perímetro de un cuadrado es el doble del lado:

Perímetro de un cuadrado = 4 a

Rombo

El rombo es un paralelogramo con sus lados adyacentes de la misma longitud, pero como en un paralelogramo los lados opuestos son iguales entonces, todos los lados de un rombo son de igual longitud.

Las diagonales de un rombo son de longitud diferente, pero se cortan en ángulo recto.

Ejemplos

Ejemplo 1

Demostrar que en un cuadrilátero (no cruzado) los ángulos internos suman 360º.

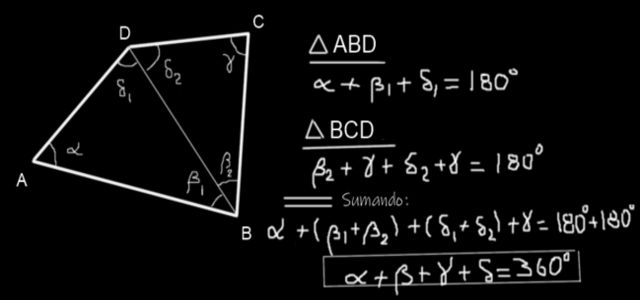
Se considera un cuadrilátero ABCD (ver figura 10) y se traza la diagonal BD. Se forman dos triángulos ABD y BCD. La suma de los ángulos internos del triángulo ABD es:

α + β₁ + δ₁ = 180º

Y la suma de los ángulos internos del triángulo BCD es:

 β2 + γ  + δ₂ = 180º

Sumando las dos ecuaciones se obtiene:

α + β₁ + δ₁ +  β₂ + γ + δ₂ = 180º + 180º

Agrupando:

α + (β₁ +  β₂) + (δ₁ + δ₂) + γ = 2* 180º

Agrupando y renombrando, finalmente se demuestra que:

α + β + δ+ γ = 360º

Ejemplo 2

Demostrar que la mediana de un trapecio es paralela a sus bases y su longitud es la semisuma de las bases.

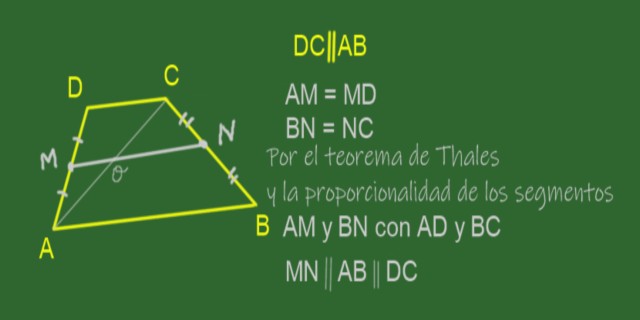
La mediana de un trapecio es el segmento que une los puntos medios de sus laterales, es decir los lados no paralelos. En el trapecio ABCD mostrado en la figura 11 la mediana  es MN. 

Por ser M punto medio de AD y N punto medio de BC, se cumple que los cocientes AM / AD y BN / BC son iguales.

Es decir, AM es proporcional a BN en la misma proporción que AD es a BC, por lo que se dan las condiciones para la aplicación del teorema (recíproco) de Thales que afirma lo siguiente:

“Si en tres o más rectas cortadas por dos secantes se determinan segmentos proporcionales, entonces dichas rectas son todas paralelas”.

En nuestro caso se concluye que las rectas MN, AB y DC son paralelas entre sí, por tanto:

“La mediana de un trapecio es paralela a sus bases”.

Ahora se aplicará el teorema de Thales:

“Un conjunto de paralelas cortadas por dos o más secantes determinan segmentos proporcionales”.

En nuestro caso AD = 2 AM, AC = 2 AO, por lo que el triángulo DAC es semejante al triángulo MAO, y consecuentemente DC = 2 MO.

Un argumento similar permite afirmar que CAB es semejante a CON, donde CA = 2 CO y CB = 2 CN. De inmediato se deduce que AB = 2 ON.

En resumen, AB = 2 ON y DC = 2 MO. Así que al sumar nos queda:

AB + DC = 2 ON + 2 MO = 2 ( MO + ON )= 2 MN

Finalmente se despeja MN:

MN = (AB + DC) /2

Y se concluye que la mediana de un trapecio mide la semisuma de las bases, o dicho de otra manera: la mediana mide la suma de las bases, dividida entre dos.

Ejemplo 3

Demostrar que en un rombo las diagonales se cortan en ángulo recto.

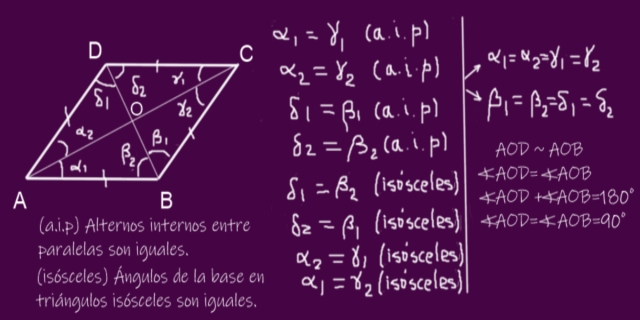
La pizarra de la figura 12 muestra la construcción necesaria. Primero se traza el paralelogramo ABCD con AB = BC, es decir un rombo. Las diagonales AC y DB determinan ocho ángulos mostrados en la figura.

Usando el teorema (a.i.p.) que afirma que ángulos alternos internos entre paralelas cortadas por una secante determinan ángulos iguales, podemos establecer lo siguiente:

α₁ = γ₁, α2 = γ2, δ₁ =  β₁ y δ2 = β2. (*)

Por otra parte, como los lados adyacentes de un rombo son de igual longitud, se determinan cuatro triángulos isósceles:

DAB, BCD, CDA y ABC

Ahora se invoca el teorema de los triángulos (isósceles) que afirma que los ángulos adyacentes a la base son de igual medida, de donde se concluye que:

δ₁ = β2, δ2 = β₁, α2 = γ₁ y α₁ = γ2 (**)

Si se combinan las relaciones (*) y (**) se llega a la siguiente igualdad de ángulos:

α₁ = α2 = γ₁ = γ₁ por una parte y β₁ =  β2 = δ₁ = δ2 por la otra. 

Recordando el teorema de los triángulos iguales que afirma que dos triángulos con un lado igual entre dos ángulos iguales son iguales se tiene:

AOD = AOB y consecuentemente también los ángulos ∡AOD = ∡AOB.

Luego ∡AOD + ∡AOB = 180º, pero como ambos ángulos son de igual medida se tiene 2 ∡AOD = 180º lo que implica que ∡AOD = 90º.

Es decir, queda demostrado geométricamente que las diagonales de un rombo se cortan en ángulo recto.

Ejercicios resuelto

– Ejercicio 1

Demostrar que en un trapecio rectángulo, los ángulos no-rectos son suplementarios.

Solución

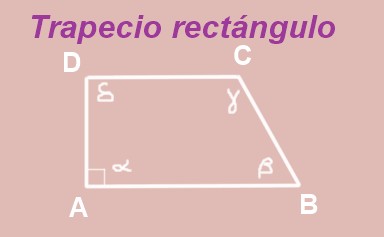
Se construye el trapecio ABCD con bases AB y DC paralelas. El ángulo interior del vértice A es recto (mide 90º), por lo que se tiene un trapecio rectángulo.

Los ángulos α y δ son ángulos internos entre dos paralelas AB y DC, por lo tanto son iguales, es decir δ = α = 90º. 

Por otra parte se ha demostrado que la suma de los ángulos internos de un cuadrilátero suma 360º, es decir:

α + β + γ + δ = 90º + β + 90º + δ = 360º.

Lo anterior conduce a:

 β + δ = 180º

Confirmando lo que se quería demostrar, que los ángulos β y δ son suplementarios.

– Ejercicio 2

Un paralelogramo ABCD tiene AB= 2 cm y AD= 1 cm, además el ángulo BAD es de 30º. Determine el área de dicho paralelogramo y la longitud de sus dos diagonales.

Solución

El área de un paralelogramo es el producto de la longitud de su base por la altura. En este caso se tomará como base la longitud del segmento b  = AB = 2 cm, el otro lado tiene longitud a = AD = 1 cm y la altura h se calculará de la siguiente manera:

h = AD * Sen(30º) = 1 cm * (1/2)= ½ cm.

Entonces: Área = b *h = 2 cm * ½ cm = 1 cm².

Referencias

1. C. E. A. (2003). Elementos de geometría: con ejercicios y geometría del compás. Universidad De Medellín.
2. Campos, F., Cerecedo, F. J. (2014). Matemáticas 2. Grupo Editorial Patria.
3. Freed, K. (2007). Discover Polygons. Benchmark Education Company.
4. Hendrik, V. (2013). Generalized Polygons. Birkhäuser.
5. IGER. (s.f.). Matemática Primer Semestre Tacaná. IGER.
6. Jr. geometry. (2014). Polygons. Lulu Press, Inc.
7. Miller, Heeren, & Hornsby. (2006). Matemática: Razonamiento Y Aplicaciones (Décima Edición). Pearson Educación.
8. Patiño, M. (2006). Matemáticas 5. Editorial Progreso.
9. Wikipedia. Cuadriláteros. Recuperado de: es.wikipedia.com