¿Qué es la velocidad lineal? (Con ejercicios resueltos)
La velocidad lineal se define como aquella que siempre es tangencial a la trayectoria seguida por la partícula, sin importar que forma tenga esta. Si la partícula siempre se mueve en un trayectoria rectilínea, no hay problema en imaginar cómo el vector velocidad va acompañando esta línea recta.
Sin embargo, en general el movimiento se lleva a cabo sobre una curva de forma arbitraria. Cada porción de la curva se puede modelar como si formara parte de una circunferencia de radio a, la cual en todo punto es tangente a la trayectoria seguida.
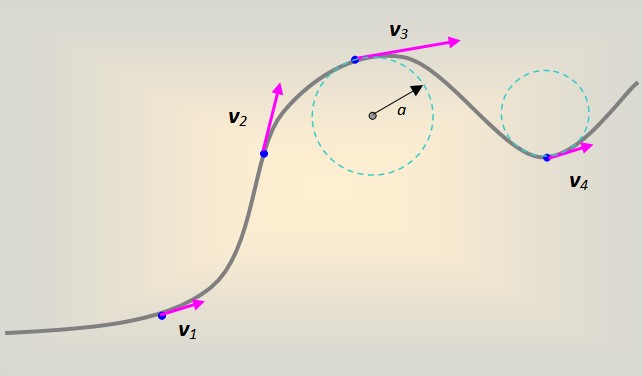
En este caso, la velocidad lineal va acompañando tangencialmente y en todo momento a la curva en cada punto de ella.
Matemáticamente la velocidad lineal instantánea es la derivada de la posición con respecto al tiempo. Sea r el vector de posición de la partícula en un instante t, entonces la velocidad lineal viene dada por la expresión:
v = r’ (t) = dr / dt
Esto significa que la velocidad lineal o velocidad tangencial, como también se la suele llamar, no es otra cosa que el cambio de la posición respecto al tiempo.
Índice del artículo
Cuando el movimiento es sobre una circunferencia, podemos ir junto a la partícula en cada punto y ver lo que sucede en dos direcciones muy especiales: una de ellas es la que apunta siempre hacia el centro. Esta es la dirección radial.
La otra dirección importante es la que transcurre sobre la circunferencia, esta es la dirección tangencial y la velocidad lineal siempre la tiene.
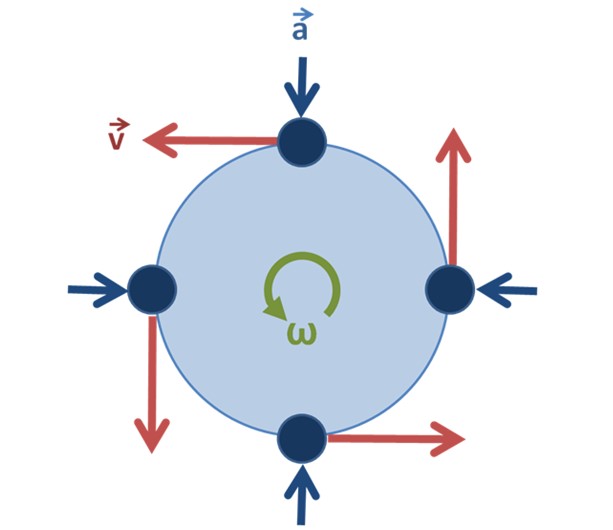
En el caso del movimiento circular uniforme, es importante darse cuenta de que la velocidad no es constante, ya que el vector va cambiando su dirección a medida que la partícula gira, pero su módulo (el tamaño del vector), que es la rapidez, sí permanece invariable.
Para este movimiento la posición en función del tiempo está dada por s (t), donde s es el arco recorrido y t es el tiempo. En ese caso la rapidez instantánea viene dada por la expresión v = ds/dt y es constante.
Si la magnitud de la velocidad también varía (ya sabemos que la dirección siempre lo hace, de lo contrario el móvil no podría dar vueltas), estamos ante un movimiento circular variado, durante el cual móvil además de girar, puede frenar o acelerar.
El movimiento de la partícula también se puede ver desde el punto de vista del ángulo barrido, en vez de hacerlo desde el arco recorrido. En tal caso se habla de la velocidad angular. Para un movimiento sobre una circunferencia de radio R, hay una relación entre el arco (en radianes) y el ángulo:
s = R θ
Derivando respecto al tiempo a ambos lados:
ds/dt = R(dθ/dt)
Llamando a la derivada de θ con respecto a t como velocidad angular y denotándola con la letra griega ω “omega”, se tiene esta relación:
v = ωR
Aceleración centrípeta
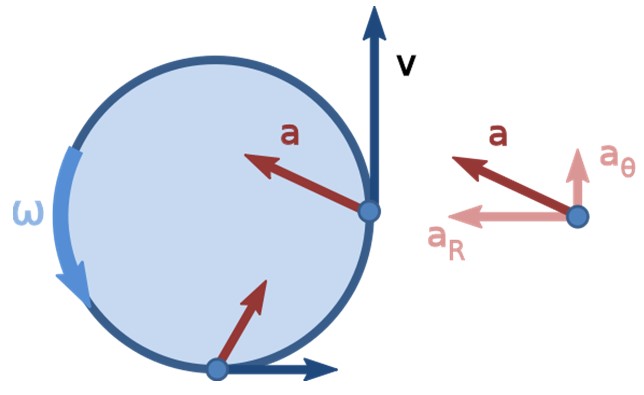
Todo movimiento circular posee aceleración centrípeta, que siempre está dirigida hacia el centro de la circunferencia. Ella se encarga de que la velocidad vaya cambiando para ir moviéndose con la partícula a medida que esta va girando.
La aceleración centrípeta ac o aR siempre apunta al centro (ver figura 2) y está relacionada con la velocidad lineal de esta forma:
ac = v2 /R
Y con la velocidad angular como:
ac = (ωR )2 /R = ω2R
Para un movimiento circular uniforme, la posición s (t) es de la forma:
s (t) = so + vt
Además el movimiento circular variado debe tener una componente de la aceleración llamada aceleración tangencialaT, que se ocupa de cambiar la magnitud de la velocidad lineal. Si aT es constante, la posición es:
s (t) = so + vot + ½ aTt2
Con vo como la velocidad inicial.
Ejercicios resueltos de velocidad lineal
Los ejercicios resueltos contribuyen a aclarar el uso adecuado de los conceptos y ecuaciones dados anteriormente.
Un insecto se mueve sobre una semicircunferencia de radio R = 2 m, partiendo del reposo en el punto A mientras aumenta su rapidez lineal, a razón de p m/s2. Encontrar: a) Al cabo de cuanto tiempo llega al punto B, b) El vector velocidad lineal en ese instante, c) El vector aceleración en ese instante.
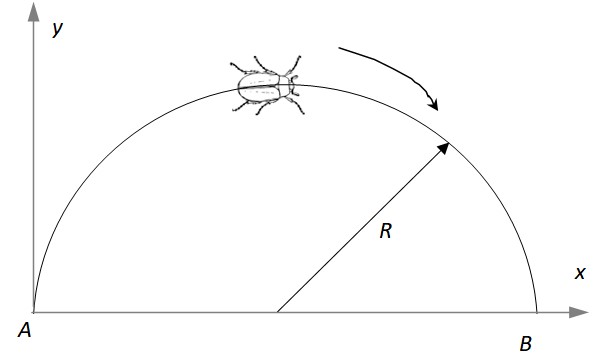
Solución
a) El enunciado indica que la aceleración tangencial es constante y vale π m/s2, luego es válido utilizar la ecuación para movimiento uniformemente variado:
s (t) = so + vot + ½ aT.t2
Con so = 0 y vo = 0:
s (t) = ½ aT.t2
s = πR (La mitad de la longitud de la circunferencia)
t = (2. πR /aT) ½ s = (2π.2 /π)½s = 2 s
b) v(t) = vo + aT. t = 2π m/s
Cuando está en el punto B, el vector velocidad lineal apunta en la dirección vertical hacia abajo en la dirección (-y):
v (t) = 2π m/s(-y)
c) Ya se tiene la aceleración tangencial, falta la aceleración centrípeta para tener el vector velocidad a:
ac =v2 / R = (2π)2 / 2 m/s2 =2π2 m/s2
a = ac (-x) + aT (-y) = 2π2(-x)+ π (-y) m/s2
Una partícula gira en un círculo de radio 2.90 m. En un instante particular su aceleración vale 1.05 m/s2 en una dirección tal que forma 32º con su dirección de movimiento. Encontrar su velocidad lineal en: a) Este momento, b) 2 segundos más tarde, suponiendo que la aceleración tangencial es constante.
Solución
a) La dirección de movimiento es precisamente la dirección tangencial:
aT = 1.05 m/s2 . cos 32º = 0.89 m/s2 ; aC = 1.05 m/s2 . sen 32º = 0.56 m/s2
La velocidad se despeja de ac = v2 / R como:
v = (R.ac)1/2 = 1.27 m/s
b) Es válida la ecuación para movimiento uniformemente variado siguiente: v = vo + aTt = 1.27 + 0.89 .22 m/s = 4.83 m/s
- Bauer, W. 2011. Física para Ingeniería y Ciencias. Volumen 1. Mc Graw Hill. 84-88.
- Figueroa, D. Serie Física para Ciencias e Ingeniería. Volumen 3ra. Edición. Cinemática. 199-232.
- Giancoli, D. 2006. Physics: Principles with Applications. 6th.. Ed Prentice Hall. 62-64.
- Relative Motion. Recuperado de: courses.lumenlearning.com
- Wilson, J. 2011. Fisica 10. Pearson Educación. 166-168.
