Función exponencial: propiedades, ejemplos, ejercicios
La función exponencial es una función matemática de gran importancia por las muchas aplicaciones que tiene. Se define de la siguiente manera:
f (x) = bx, con b > 0 y b ≠ 1
Donde b es una constante real siempre positiva y diferente de 1, a la cual se conoce como base. Nótese que la variable real x se encuentra en el exponente, de esta manera f(x) siempre es un número real.
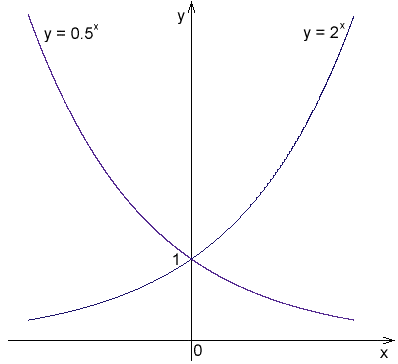
Ejemplos de funciones exponenciales son los siguientes:
-f(x) = 2x
-g(x) = 5⋅e-3x
-h(x) = 4⋅(102x)
Se trata de funciones que crecen –o decrecen, según el signo del exponente- muy rápidamente, por eso se habla del “crecimiento exponencial” cuando alguna magnitud aumenta muy deprisa. Es la razón por la cual son apropiadas para modelar el crecimiento de seres vivos, tales como bacterias.
Otra aplicación muy interesante es la del interés compuesto. Cuanto más dinero se tiene en una cuenta, más intereses devenga, y los mismos se pueden calcular cada cierto intervalo de tiempo, tan pequeño como se quiera.
Con ayuda de la función logarítmica, que es la función inversa de la exponencial, se puede saber al cabo de cuánto tiempo un cierto capital aumenta a determinado valor.
Índice del artículo
- 1 Propiedades de la función exponencial
- 2 Ejemplos de funciones exponenciales
- 3 Ejercicios resueltos
- 4 Referencias
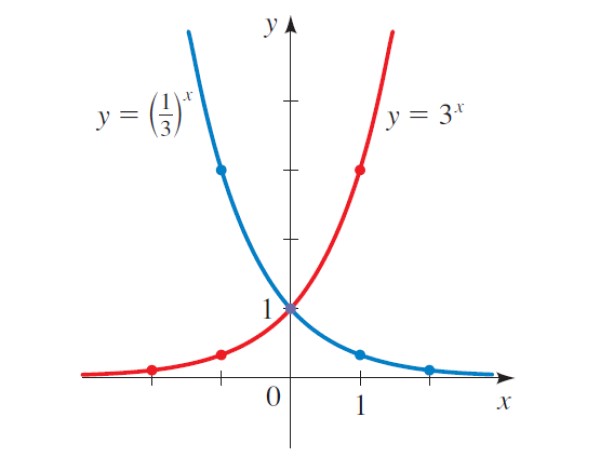
Las siguientes son las propiedades generales de cualquier función exponencial:
-La gráfica de cualquier función exponencial siempre intersecta el eje vertical en el punto (0,1), como se puede apreciar en la figura 2. Ello se debe a que b0 = 1 para cualquier valor de b.
-La función exponencial no intersecta al eje x, de hecho este eje es una asíntota horizontal para la función.
-Dado que b1 = b, el punto (1, b) siempre pertenece a la gráfica de la función.
-El dominio de la función exponencial lo constituye el conjunto de los números reales y f(x) = bx es continua en todo su dominio.
-El rango de la función exponencial son todos los números reales mayores que 0, lo cual también se advierte de la gráfica.
-La función exponencial es uno a uno, es decir, cada valor de x perteneciente al dominio de la función, tiene una imagen única en el conjunto de llegada.
-La inversa de la exponencial es la función logarítmica.
Como hemos dicho antes, la función exponencial puede ser creciente o decreciente.
Si se estudia con cuidado la gráfica de la figura 2 se advierte que si b >1, la función es creciente, por ejemplo y = 3x, pero en el caso de y = (1/3)x, con b 1, la función decrece.
Tenemos entonces dos tipos de funciones exponenciales con las siguientes propiedades particulares:
Para b > 1
-La función siempre es creciente.
-Cuando aumenta el valor de b, la función crece más rápido, por ejemplo y = 10x crece más rápido que y = 2x.
–Cuando la variable es mayor que 0, la función adquiere valores mayores que 1, es decir:
Para x > 0: y > 1
-Y si x0, entonces f(x) 1.
Para b 1
-La función es siempre decreciente.
-Al disminuir el valor de b, la función decrece más rápido aún. Por ejemplo y = (1/5)x decrece más rápidamente que y = (1/3)x.
-Para valores de x menores que 0, la función toma valores mayores a 1, es decir:
Para x 0: y >1
-Finalmente, cuando x > 0, entonces y 1.
La función exponencial es muy útil para modelar fenómenos en ciencia y economía, como veremos a continuación:
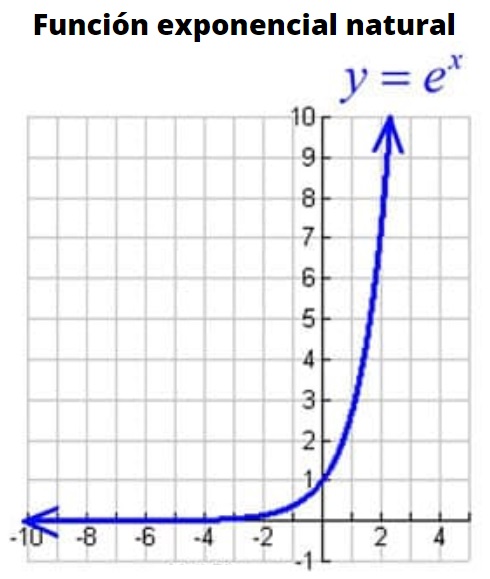
Es la función cuya base es el número e o número de Euler, un número irracional cuyo valor es:
e =2.718181828…
Esta base, aunque no sea un número redondo, funciona muy bien para numerosas aplicaciones. Por lo tanto se considera la base más importante de todas las funciones exponenciales. La función exponencial natural se expresa en forma matemática como:
f (x) = ex
La función exponencial aparece con frecuencia en Probabilidad y Estadística, ya que diversas distribuciones de probabilidad, como la distribución normal, la de Poisson y otras, se pueden expresar a través de funciones exponenciales.
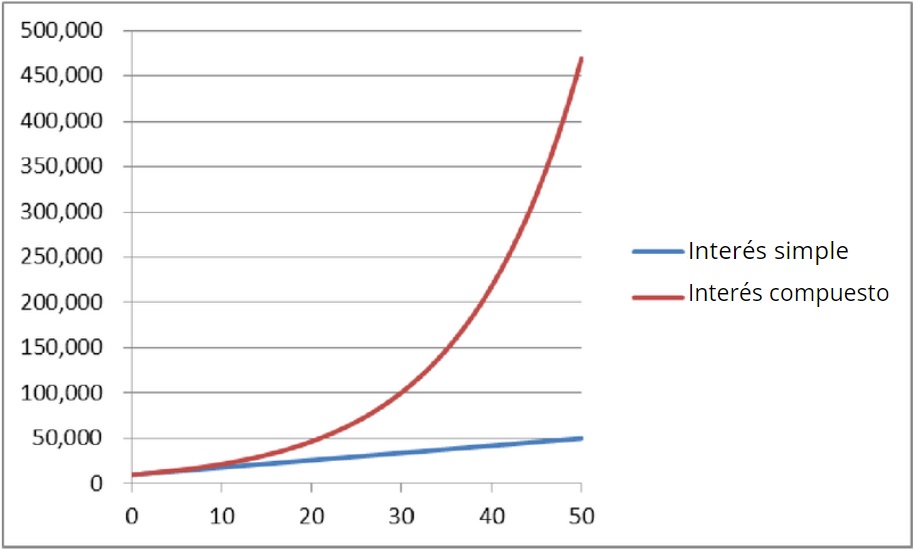
También se le llama capitalización continua. Para conocer la cantidad de dinero A que se tiene al cabo de t años, se emplea la expresión exponencial:
A (t) = P ⋅ ert
Donde P es la cantidad de dinero originalmente depositada, r es la tasa de interés al año y finalmente t es el número de años.
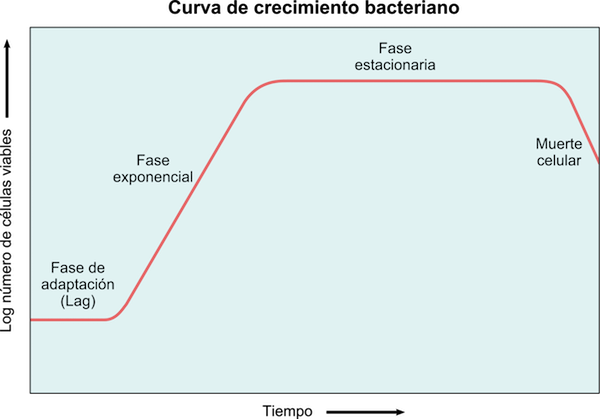
Las bacterias crecen exponencialmente, así que el crecimiento puede modelarse mediante:
N (t) = No ⋅ e kt
Donde N (t) es la población existente al cabo del tiempo t (casi siempre en horas), No es la población inicial y k es una constante que depende del tipo bacteria y las condiciones en las que se cultiva, por ejemplo los nutrientes disponibles.
Ciertos núcleos en la naturaleza son inestables, por lo que decaen para transformarse en otros más estables, un proceso que puede ser muy breve o tomar miles de años, dependiendo del isótopo. Durante el decaimiento radiactivo se emiten partículas y en ocasiones también fotones.
Algunos isótopos radiactivos tienen aplicaciones médicas, por ejemplo el yodo radiactivo I-131, que emplean los médicos en el diagnóstico y tratamiento de ciertas afecciones tiroideas.
El decaimiento radiactivo se modela mediante una función exponencial.
Las ecuaciones en las cuales la incógnita aparece como exponente se denominan ecuaciones exponenciales. Para despejar el valor de la incógnita se recurre a distintas manipulaciones algebraicas y al uso de la función logaritmo, que es la función inversa de la exponencial.
Veamos algunos ejercicios resueltos que ilustran el punto.
Resolver las siguientes ecuaciones exponenciales:
a) 5x = 625
b) 5x = 2x-1
Solución a
El número 625 es múltiplo de 5, en efecto, al descomponerlo encontramos que:
625 = 54
Por lo tanto podemos escribir:
5x = 54
Ya que las bases son iguales tanto a la izquierda como a la derecha, podemos igualar los exponentes y obtener:
x = 4
Solución b
Para este ejercicio no podemos recurrir a la técnica empleada previamente, ya que las bases no son las mismas. Pero podemos aplicar logaritmo a ambos lados de la igualdad, de esta manera:
5x = 2x-1
log (5x) = log (2x-1)
Ahora se aplica la siguiente propiedad de los logaritmos:
log mn = n⋅log m
Y queda:
x⋅log 5 = (x-1)⋅log 2
x⋅(log 5 – log 2) = -log 2
x = – log 2 ÷ (log 5 – log 2)
Indicar a qué función corresponde cada una de las gráficas mostradas a continuación:
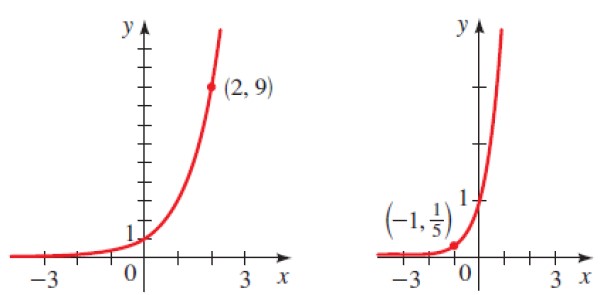
Solución a
Como se trata de una gráfica creciente, b es mayor que 1 y sabemos que el punto (2,9) pertenece a la gráfica, por lo tanto:
y = bx → 9 = b2
Sabemos que 32 = 9, por lo tanto b = 3 y la función es y = 3x
Solución b
Nuevamente sustituimos el punto dado (-1, 1/5) en y = bx para obtener:
1/5 = b-1 = 1/b
Entonces b = 5 y la función buscada es:
y = 5x
- Figuera, J. 2000. Matemática 1ro. Diversificado. ediciones CO-BO.
- Gid Hoffmann, J. Selección de Temas de Matemática para 4to. Año. Ed. Sphinx.
- Jiménez, R. 2008. Álgebra. Prentice Hall.
- Larson, R. 2010. Cálculo de una variable. 9na. Edición. McGraw Hill.
- Stewart, J. 2006. Precálculo: Matemáticas para el Cálculo. 5ta. Edición. Cengage Learning.
