Ley de Grashof: casos, mecanismos, ejemplos, aplicaciones
La ley de Grashof establece que: En un mecanismo plano de cuatro barras articuladas con una de ellas fija, por lo menos una de las barras podrá hacer un giro completo, siempre que la suma de la barra más corta y la barra más larga, sea menor o igual que la suma de las otras dos.
Hay cinco mecanismos planos de cuatro barras o eslabones que cumplen la ley de Grashof (En la figura 1 se muestra un ejemplo). Para que las barras o eslabones de los mecanismos que cumplen la ley puedan dar el giro completo es necesario que en un arreglo real, cada barra esté ocupando planos paralelos diferentes.
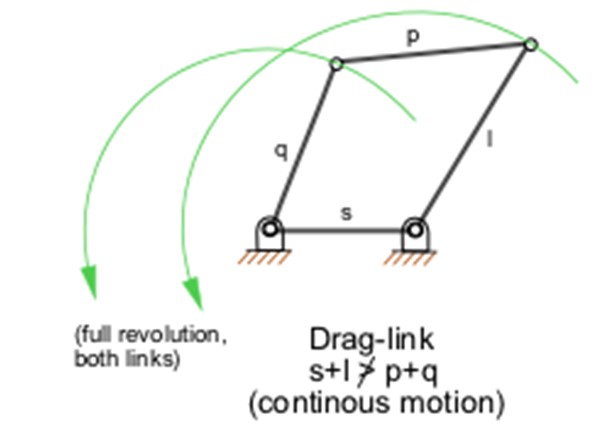
La ley de Grashof es una regla sencilla que permite diseñar un mecanismo en el que se requiera rotación completa, ya sea porque se conectará un motor o, por el contrario, porque se quiere transformar un movimiento oscilatorio en rotatorio, de forma tal que sea matemática y físicamente viable.
Índice del artículo
Supongamos que las cuatro barras articuladas tienen las siguientes longitudes ordenadas de menor a mayor según:
s > p > q > l
La ley de Grashof establece que para que al menos una barra o eslabón pueda completar una revolución o vuelta debe cumplirse la condición:
s + l = p + q
Esta desigualdad tiene las siguientes implicaciones:
– La única barra o eslabón que puede dar revoluciones completas respecto de otra es la barra más corta.
– Si la barra más corta da vueltas completas respecto de otra, entonces también dará vueltas completas respecto a todas las demás.
El movimiento del cuadrilátero articulado que cumpla la ley de Grashof puede ser de los siguientes tipos:
– De doble vuelta o manivela, si la barra más corta es el fija y las barras adyacentes dan vueltas completadas.
– Vuelta y de vaivén, si la barra corta es adyacente a la barra fija.
– Doble balancín, siempre que la barra más corta esté opuesta a la fija.
Cuando se cumple la igualdad en la fórmula de Grashof, entonces se está en el caso límite en el que la suma de la barra más corta con las más larga, es igual a la suma de las otras dos.
En este caso, el mecanismo puede adoptar una configuración en el que las cuatro barras quedan alineadas. Y es en esta posición, las articulaciones no fijas pueden indiferentemente ir en un sentido o el otro, haciendo que el mecanismo pueda trabarse.
Los mecanismos que cumplen la condición de Grashof son más confiables y sufren menos tensiones en sus articulaciones y eslabones, en la medida que estén más lejos del caso límite de la igualdad.
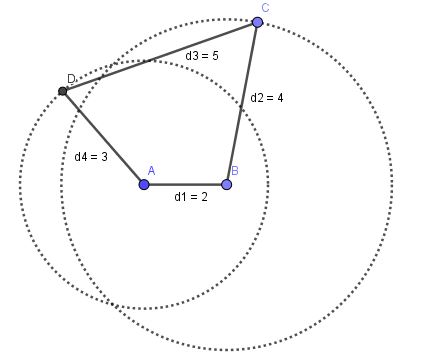
Denotaremos las articulaciones consecutivas con A, B, C y D, entonces:
– A y B son pivotes fijos.
– AB = d1 (barra fija)
– BC= d2
– CD= d3
– DA= d4
Las barras b2 y b4 giran completamente y se cumple la ley de Grashof:
d1+d3 = d2+d4.
A continuación, se nombran y describen las características de otros mecanismos que cumplen la ley de Grashof:
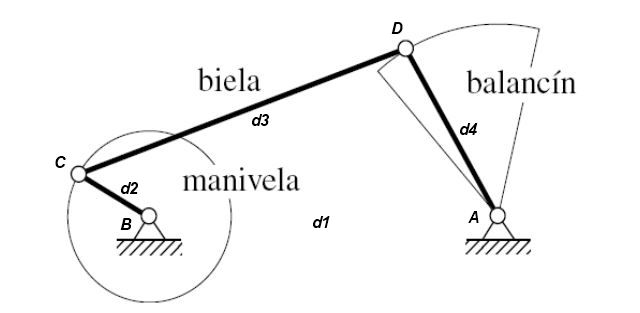
Mecanismo manivela – balancín
Se cumple d2 + d3 = d1 + d4
La barra más corta d2 gira completamente y la barra opuesta d4 hace un movimiento de balancín.
Mecanismo de doble balancín
– La barra fija AB es mayor que la barra opuesta CD y cumple que:
d1 + d3 = d2 + d3
– Para la barra más corta (la opuesta a la barra fija), es capaz de dar un giro completo.
Mecanismo de paralelogramo articulado
– Las barras AD y BC son de igual longitud y siempre paralelas.
– Por su parte, las barras AB y CD son de igual longitud y siempre paralelas.
– En el caso de las barras opuestas, estas tienen la misma longitud y se cumple d1 + d2 = d3 +d4, de acuerdo a la ley de Grashof.
– Finalmente, las barras AD y BC giran completamente en el mismo sentido.
Anti-Paralelogramo articulado
– Las barras AD y BC son de igual longitud y no paralelas.
– Para las barras AB y CD, estas deben ser de igual longitud y no paralelas.
– Por su parte, las barras opuestas tienen la misma longitud, dos de ellas van cruzadas.
– En este mecanismo se debe tener la siguiente condición:
d1 + d2 = d3 +d4
– El giro de las barras AD y BC es completo pero de sentidos opuestos.
Los mecanismos que cumplen la ley de Grashof tienen múltiples aplicaciones:
Se aplica a la máquina de coser de pedal, útil en los lugares donde no hay electricidad, en la que el pedal hace un movimiento de vaivén o balancín, que se transmite a una rueda conectada mediante una polea a la máquina de coser.
Otro ejemplo a mencionar es el mecanismo de los limpiaparabrisas. En este, un motor va conectado a la barra manivela que realiza giros completos, transmitiendo un movimiento de balancín a la barra que mueve el primer cepillo del sistema.
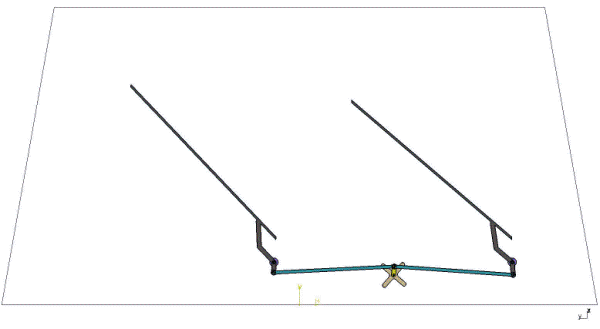
Otra aplicación del mecanismo de manivela – balancín son los balancines para bombear petróleo del subsuelo.

Un motor va conectado a la manivela que gira completamente y transmite el movimiento al cabezal o balancín de bombeo.
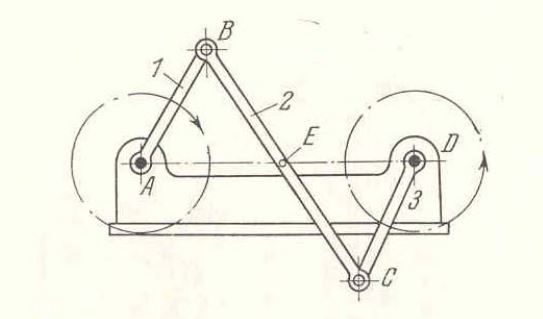
Este mecanismo solía emplearse para conectar las ruedas de las locomotoras de vapor, de modo que ambas ruedas giren en el mismo sentido y a la misma velocidad.
La característica principal de este mecanismo es que la barra que conecta ambas ruedas tiene la misma longitud que la separación de los ejes de las mismas.
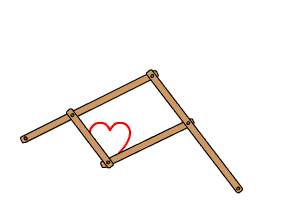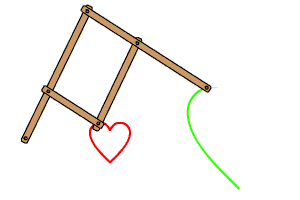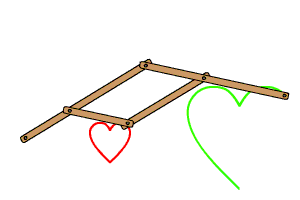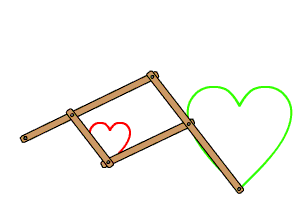
El pantógrafo es un instrumento de dibujo que se usa para copiar y ampliar imágenes. Está basado en un mecanismo de cuatro barras, en el que hay cuatro articulaciones que forman los vértices de un paralelogramo.
Es el mecanismo que se usa en la máquina lanzadora de pelotas de tenis, donde se requieren que las ruedas que impulsan y lanzan la pelota giren en sentidos contrarios.
- Clemente C. Laboratorio virtual de un mecanismo manivela – balancín. Trabajo de grado en ingeniería mecánica. Universidad de Almería. (2014). Recuperado de: repositorio.ual.es
- Hurtado F. Ley de Grashof. Recuperado de: youtube.com
- Mech Designer. Kinematics Grashof criterion. Recuperado de: mechdesigner.support.
- Shigley, J. Teoría de máquinas y mecanismos. Mc-Graw Hill.
- Somos F1. Análisis de mecanismo de cuatro barras. Recuperado de: youtube.com
- UNAM. Desarrollo de un mecanismo de cuatro barras para su uso en la enseñanza. Recuperado de: ptolomeo.unam.mx
- Wikipedia. Four-bar linkage. Recuperado de: en.wikipedia.com
- Wikipedia. Ley de Grashof. Recuperado de: es.wikipedia.com
