Multiplicación de fracciones: cómo se hace, ejemplos, ejercicios
La multiplicación de fracciones es una operación aritmética entre dos o más fracciones que da lugar a una nueva fracción. Su numerador se halla multiplicando los numeradores de las fracciones participantes, y el denominador se encuentra de la misma manera.
Vamos a verlo con un ejemplo en la siguiente imagen. Supongamos que se tienen dos fracciones a/b y c/d, con b y d distintos de 0.

Para llevar a cabo la multiplicación entre ellas se efectúa el producto entre los numeradores y también el de los denominadores. De esta manera se crea una nueva fracción donde el numerador y el denominador son, respectivamente: (a × c) y (b × d).
Este procedimiento se extiende fácilmente a la multiplicación de tres y más fracciones. Veamos más detalles a continuación.
¿Cómo se hace la multiplicación de fracciones?
El producto se puede simbolizar con una cruz o bien con un punto intercalado entre las fracciones. Además hay que tomar en cuenta que las fracciones pueden tener signo positivo o signo negativo, por lo que es preciso tener cuidado de seguir la regla de los signos:
-Cuando se multiplican dos números de igual signo el producto es positivo.
-Si se multiplican dos cantidades de signos diferentes, el resultado es negativo.
De esta manera:
Si numerador y denominador de las fracciones participantes no son primos entre sí, conviene simplificarlos antes de hacer la multiplicación de fracciones. De esta forma se obtienen números más pequeños y manejables al momento de ejecutar los productos.
Propiedades de la multiplicación de fracciones
Producto por 0
Cualquier fracción multiplicada por 0 es igual a 0:
Producto por 1
Toda fracción multiplicada por 1 es igual a sí misma:
Por ello el 1 se considera el elemento neutro de la multiplicación. Obsérvese que el número entero 1 tiene una expresión fraccionaria:
De tal manera que podemos multiplicar al 1 por cualquier fracción, mediante la regla ya explicada. Así:
Propiedad conmutativa
La multiplicación de fracciones es conmutativa, lo cual significa que el orden de los factores no altera el producto:
Propiedad asociativa
La multiplicación de fracciones también es asociativa, lo podemos comprobar multiplicando tres fracciones:
Donde, como siempre, los denominadores b, d y f son distintos de 0.
En palabras: si vamos a multiplicar tres fracciones, podemos elegir hacer el producto de las dos primeras, y multiplicar el resultado por la tercera fracción. O bien multiplicar las dos últimas y su resultado multiplicarlo finalmente por la primera de las fracciones.
Cualquiera que sea el orden escogido, el resultado será el mismo. Vamos a comprobarlo:
Para realizar la operación se multiplicaron las dos primeras fracciones de izquierda a derecha. El resultado se multiplicó a su vez por la tercera fracción para obtener el resultado final.
La otra alternativa es multiplicar las dos últimas fracciones, dejando en espera la primera. El lector puede apreciar que el resultado intermedio consiste en dos fracciones diferentes a las que se obtuvieron de la otra manera. Pero el resultado final es el mismo:
Propiedad distributiva respecto a la suma
Sean tres fracciones a/b, c/d y e/f, con b, d y f diferentes de 0. La multiplicación es distributiva respecto de la suma.
Supongamos que queremos efectuar la siguiente operación:
La manera de llevarla a cabo, mediante esta propiedad, es la siguiente:
Por lo tanto, el producto de un número por la suma de otros dos, se puede efectuar sumando dos productos: el primero por el segundo y el primero por el tercero. Resulta muy sencillo mediante un ejemplo:
El resultado final aparece simplificado al máximo, tal como se explicó más arriba.
Ejemplos
Multiplicación de una fracción por un entero
Supongamos que se desea multiplicar una fracción a/b por un entero n:
Anteriormente vimos que el número 1 se puede expresar como fracción, simplemente colocando como denominador al 1. Podemos hacer lo mismo con cualquier entero n, ya que dividirlo entre 1 no lo altera en absoluto. Entonces:
Por ejemplo:
Ejemplo 2: multiplicación de una fracción por un número mixto
Un número mixto o fracción mixta, es aquel que tiene una parte entera y una parte fraccionaria. Para efectuar el producto de un número así, ya sea con una fracción, otro número mixto o con un número entero, es preciso transformarlo a su vez en fracción.
La fracción que representa a un número mixto es una fracción impropia, una cuyo numerador tiene mayor valor absoluto que el denominador.
Podemos obtenerla a través de la suma de la parte entera, convenientemente expresada como fracción colocando un 1 como denominador, más la parte fraccionaria.
En la imagen hay un ejemplo de número mixto, que demuestra lo frecuentes que son. Tenemos 2 vasos y medio de agua, que como número mixto se expresa así:
2 ½
Obtenemos la fracción impropia que lo representa:
Ejercicios resueltos
Ejercicio 1
Efectuar la siguiente operación:
Solución
El número 1 ¾ es un número mixto. Su parte entera es 1 y su parte fraccionaria es ¾. Si efectuamos la operación: 1 + ¾, el número mixto se transforma en una fracción impropia.
1 + ¾ = (4+3) /4 = 7/4
Una vez transformado el número mixto a fracción impropia, la operación de multiplicación se lleva a cabo como de costumbre:
Ejercicio 2
La edad de José es ½ de los 2/3 de la edad de Manuel. Si Manuel tiene 24 años, ¿Cuál es la edad de José?
Solución
Sea x la edad de José, una incógnita que debemos encontrar. El enunciado nos dice que la edad de Manuel es 24 años, por lo tanto este valor es conocido.
Para determinar la edad de José, llevemos a cabo las operaciones que nos indica el enunciado: “La edad de José es ½ de los 2/3 de la edad de Manuel”.
Se trata de la multiplicación de dos fracciones por un número entero:
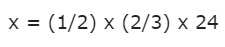
Podemos multiplicar las dos primeras fracciones de acuerdo a las reglas descritas antes. Por su parte, el número 24 es un entero, pero ya sabemos que no hay problema en transformarlo a una fracción, simplemente colocando un 1 como denominador:
Esto es lo que nos queda después de la cancelación:
Referencias
- Baldor, A. 1986. Aritmética. Ediciones y Distribuciones Códice.
- Carena, M. 2019. Manual de Matemática. Universidad Nacional del Litoral.
- Jiménez, R. 2008. Álgebra. Prentice Hall.
- Sangaku Maths. Multiplicación de fracciones. Recuperado de: sangakoo.com.
- Smartick. Multiplicación de fracciones. Recuperado de: smartick.es.
