Ecuaciones fraccionarias: qué son, cómo resolverlas, ejemplos de ejercicios y ejercicio resuelto

¿Qué son las ecuaciones fraccionarias?

Las ecuaciones fraccionarias son aquellas que contienen fracciones en uno o más de sus términos. Tales fracciones pueden ser numéricas o algebraicas, donde la incógnita puede encontrarse en el numerador y/o en el denominador de cualquier término.

Seguidamente, algunos ejemplos de ecuaciones fraccionarias con una sola incógnita:

El primer ejemplo es una ecuación lineal con coeficientes fraccionarios; en el segundo ejemplo, la incógnita está en el denominador de cada uno de los términos, y en el último, la incógnita está tanto el numerador como en el denominador.

Para resolverlas, es preciso llevar a cabo algunas transformaciones algebraicas y obtener así una ecuación equivalente, en la cual la incógnita no aparezca en el denominador. Una vez realizado este procedimiento, se halla la solución empleando las técnicas apropiadas.

La solución consiste en el conjunto de valores de “x” que satisfacen la igualdad. Puede ser un valor único, o varios, pero, en cualquier caso, es muy importante tener presente que no todas las soluciones de la ecuación equivalente son aceptables para la ecuación original.

En efecto, si se trata de una ecuación cuya incógnita está en el denominador, hay que evitar los valores de “x” que lo anulen, aun si pertenecen al conjunto de soluciones de la ecuación equivalente. Esto se debe a que la división entre 0 no está definida.

Si la ecuación equivalente tiene una solución única, y resulta que esta anula el denominador de alguno de los términos de la ecuación original, entonces esta no tiene solución.

Cómo resolver una ecuación fraccionaria

Son válidas las operaciones que se llevan a cabo para resolver ecuaciones no fraccionarias, siempre que la igualdad se mantenga. De esta forma, en una ecuación fraccionaria se puede sumar o restar la misma cantidad a ambos lados de la igualdad, multiplicar todos los términos por una misma cantidad, o dividir cada término por la misma cantidad (distinta de 0).

Pero como es preciso transformar la ecuación fraccionaria en otra equivalente sin denominadores, se siguen además las siguientes indicaciones de carácter general:

1. Hallar el mínimo común múltiplo de los denominadores (m.c.m).
2. Multiplicar cada término por el m.c.m., con la finalidad de eliminar los denominadores.
3. Resolver la ecuación equivalente obtenida.
4. Verificar que las soluciones encontradas satisfacen la igualdad original.

Tipos de ecuaciones equivalentes

Las ecuaciones equivalentes obtenidas siguiendo el procedimiento señalado pueden ser:

• Lineales o de primer grado
• Cuadráticas
• De orden superior

Ejemplos resueltos

Ejemplo 1

Resolver la siguiente ecuación:

Se advierte que la ecuación es de primer grado en “x”, pues “x” está elevada a la 1. Los coeficientes de la ecuación son fracciones y una forma de eliminarlos, para trabajar con números enteros, es multiplicando todos los términos por el mínimo común múltiplo de los denominadores (m.c.m.).

m.c.m. (2,3,6) = 6

Entonces:

3x – 2x=1

x=1

El lector puede comprobar la validez de esta solución, sustituyendo x = 1 en la ecuación original y verificando que se obtiene una igualdad.

Ejemplo 2

Determinar los valores de “x” que satisfacen:

A diferencia del ejemplo anterior, en este caso la incógnita se encuentra en el denominador. Nótese que los denominadores se anulan para los valores x = 2 y x = −1, un detalle que es conveniente tener en cuenta, ya que, si la ecuación equivalente admite estas soluciones, hay que desecharlas, pues no son admisibles en la ecuación original.

Ahora hay que transformar la ecuación en otra sin denominadores, el primer paso es efectuar la suma de términos a la izquierda de la igualdad:

Como los denominadores son iguales, para que la igualdad se cumpla es preciso que los numeradores también lo sean:

4(x+1) – 3(x–2) = 8

Basta con resolver esta ecuación, que resulta ser de primer grado:

4x + 4 – 3x + 6 = 8

x = 8 – 6 – 4 = – 2

x = – 2

Dado que este valor es distinto a los valores prohibidos, se admite como solución de la ecuación original.

Ejemplo 3

Hallar la solución de:

En esta ecuación, el valor x = 4 anula los denominadores, por lo tanto, se excluye del conjunto solución de la ecuación transformada, si acaso apareciera.

La ecuación transformada es fácil de hallar, basta multiplicar todos los términos por el factor (x–4):

Quedando:

2x – 4 = 4

2x = 8

x = 4

Ejemplo 4

Resolver la ecuación:

En este caso, los denominadores tienen términos cuadráticos, así que conviene factorizarlos primero:

• x² + 8x + 7 = (x + 7)(x + 1)
• x² − 49 = (x + 7)(x − 7)
• x² − 6x − 7 = (x − 7)(x + 1)

La ecuación queda así:

Los valores de x que anulan a cualquiera de los denominadores son: x = −7, x = 7, x = −1. Por tanto, aun si estos valores forman parte del conjunto solución de la ecuación modificada, no pueden ser solución de la ecuación original.

Ahora viene el proceso de transformar la ecuación. El primer paso es encontrar el mínimo común múltiplo de los denominadores:

m.c.m. = (x + 7)(x − 7)(x + 1)

Al multiplicar a ambos lados de la igualdad por el m.c.m. queda:

Resultando:

(x−7)(x− 2) = (x + 1)(2x – 5) – (x+7)(x−2)

Mediante la propiedad distributiva se desarrollan los productos:

x² – 9x +14 = 2x² – 3x – 5 – (x² + 5x – 14)

Reduciendo términos semejantes en el lado derecho:

x² – 9x + 14 = x² – 8x + 9

Los términos cuadráticos se cancelan, por encontrarse con el mismo signo en distintos lados de la igualdad:

– 9x + 14 = – 8x + 9

–x = –5 ⇒ x = 5

Se admite como solución este resultado, ya que no es alguno de los valores prohibidos.

Ejercicio de aplicación de las ecuaciones fraccionarias

El denominador de una fracción excede en cuatro unidades al numerador. Si al numerador se le restan 5 unidades al numerador y al denominador también, la fracción resultante es 3/5. Determinar la fracción original.

Solución

Sea x el valor del numerador.

Dado que el denominador de la fracción excede en cuatro unidades al numerador, la fracción original es:

Ahora hay que restar 5 unidades, tanto al numerador como al denominador:

Puesto que la fracción resultante de llevar a cabo el procedimiento anterior es igual a 3/5, se igualan:

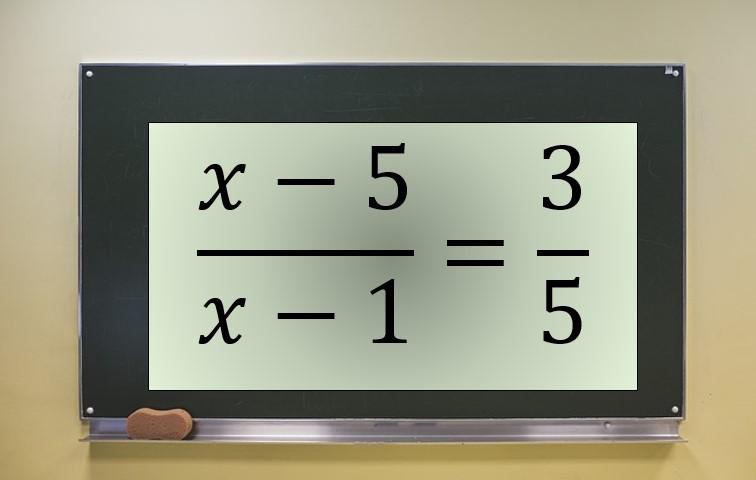
Esta es una ecuación fraccionaria con la incógnita en numerador y denominador, el cual se anula en x = 1. Por lo tanto, este valor debe excluirse, si acaso estuviera entre las soluciones de la ecuación transformada.

Seguidamente, se multiplica a ambos lados por el mínimo común múltiplo, que es 5(x−1):

Resultando la siguiente ecuación equivalente:

5(x−5) =3(x−1)

Aplicando propiedad distributiva:

5x –25 = 3x – 3 ⇒ 2x = 22

x = 11

La fracción original se halla sustituyendo x = 11 en la expresión:

Lo que resulta en la fracción 11/15. Esta es la respuesta al problema planteado.

Referencias

1. Ecuaciones fraccionarias. Recuperado de: mathepower.com
2. Portal de Matemáticas. Ecuaciones fraccionarias. Resolución de problemas. Recuperado de: silvioduarte.com.
3. Stewart, J. (2007). Precálculo: Matemáticas para el Cálculo. 5ta. Edición. Cengage Learning.
4. Sullivan, M. (1997). Precálculo. 4ta. Edición. Pearson Educación.
5. Zill, D. (2008). Precálculo con avances de Cálculo. 4ta. Edición. McGraw Hill.